
Электричество и магнетизм. Методические указания по физике для студентов всех специальностей. Белко В.Н., Тарханов А.К
.pdfФедеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Воронежский государственный архитектурно - строительный университет
Кафедра физики
Электричество и магнетизм
Методические указания к решению задач по физике
для студентов всех специальностей дневной, заочной и ускоренной форм обучения
Воронеж – 2009
Составители В.Н. Белко, А.К. Тарханов
УДК 53.07
Электричество и магнетизм: Метод. указания по физике для студ. всех спец. дневной, заочной и ускоренной форм обучения / Воронеж гос. арх.-строит. ун-т; сост.: В.Н. Белко, А.К. Тарханов. – Воронеж, 2009. – 34 стр.
Методические указания предназначены для студентов полной и сокращенной форм обучения. Приведены примеры решения и условия задач по темам «Электростатика», «Постоянный ток», «Электромагнетизм». Ко всем задачам приведены ответы.
Ил.: 11. Библиогр.: 5 назв.
Печатается по решению редакционно-издательского Совета Воронежского государственного архитектурно-строительного университета
Рецензент – Авдеев В.П., проф., докт. физ.-мат. наук, кафедра ММиВТ, ВГACУ
2
Введение
Физика относится к числу естественных наук. Предметом физики является изучение наиболее общих свойств материи, т.е. вещества и поля, наиболее общих закономерностей и форм ее движения.
Физика позволяет создавать приборы и вырабатывать методы исследования, необходимые для успешного развития всех естественных и прикладных наук (так, например, выдающуюся роль в развитии ряда наук сыграли микроскоп, телескоп, спектральный анализ, рентгенография и т.п.). Существуют и специальные дисциплины: астрофизика, физическая химия, биофизика, агрофизика, металлофизика, строительная физика и др., возникшие на стыках физики и других наук. Поэтому можно утверждать, что физика есть фундамент, на котором строятся все естественные и прикладные науки.
Изучение физики в высших учебных заведениях преследует двоякую
цель:
1)расширить кругозор учащихся и способствовать развитию у них миропонимания;
2)подготовить их к сознательному изучению смежных с физикой дисциплин.
Учебная работа студента складывается из следующих основных элементов: самостоятельного изучения физики по учебным пособиям, посещения и проработки лекций, выполнения контрольных работ, прохождения лабораторного практикума, сдачи зачетов и экзаменов.
Предлагаемый материал призван помочь усвоению теоретических знаний. Самостоятельное выполнение контрольных заданий способствует более глубокому пониманию курса физики и закреплению его в памяти.
3
Электростатика.
Закон Кулона. Напряженность электрического поля. Принцип суперпозиции
Задание. Два маленьких одинаковых заряженных шарика, находящиеся на расстоянии r=0,2м друг от друга, притягиваются с силой F1= 4 10−3 H. После того, как шарики были приведены в соприкосновение и затем разведены на прежнее расстояние, они стали отталкиваться с силой F2= 2,25 10−3 H. Определить первоначальные заряды шариков.
Решение. Так как в начале шарики притягивались, то их заряды противоположны по знаку и по закону Кулона
F = −k |
q1q2 |
. |
(1) |
|
|||
1 |
r2 |
|
|
|
|
||
После того, как шарики были приведены в соприкосновение, заряды пере-
распределяются, и на каждом из шариков заряд становится равным q1 +2 q2 . По-
этому они взаимодействуют с силой
F = k |
(q + q |
)2 |
(2) |
1 2 |
. |
||
2 |
4r2 |
|
|
|
|
|
|
Решая совместно уравнения (1) и (2), находим: |
|
||
q q |
|
= − |
F r2 |
, |
(3) |
|
2 |
1 |
|||||
|
||||||
1 |
|
|
k |
|
|
|
|
|
|
|
F2 . |
|
|
q + q |
2 |
= 2r |
(4) |
|||
1 |
|
|
|
k |
|
|
|
|
|
|
|
|
|
Для определения q1 и q2 воспользуемся теоремой Виета. Согласно этой теореме и соотношениям (3) и (4), q1 и q2 – корни квадратного уравнения
x |
2 |
− 2r |
F |
x − |
F r 2 |
= 0. |
|
2 |
1 |
||||
Находим эти корни: |
|
|
k |
|
k |
|
|
|
|
|
|
|
x |
= r |
F |
± |
F r2 |
F r2 |
r |
( F |
± F + F ) , |
|||
2 |
2 |
+ |
1 |
= |
|
||||||
1,2 |
|
k |
|
k |
|
k |
|
k |
2 |
2 |
1 |
где k=9 109Ф/м. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 = |
r |
( F2 + |
F2 +F1) ≈2,67 10−7 Кл, |
|||
|
|
= r |
k |
|
|
|
|
|
q |
2 |
( |
F − |
F + F |
1 |
) ≈ −0,67 10−7 |
Кл. |
|
|
k |
|
2 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
Заметим, что в соответствии с симметрией задачи возможны и такие значения зарядов: q1 =−2,67 10−7 Кл, q2 =−0,67 10−7 Кл.
4

Работа электрических сил при перемещении зарядов. Потенциал электрического поля
Задание. Два точечных заряда q1 =5 10−9 Кл и q2 =10−8 Кл находятся на расстоянии r1 = 45 см. Какую надо совершить работу, чтобы сблизить их до расстояния r2 = 25см?
Решение. Искомая работа равна изменению потенциальной энергии зарядов, т.е. энергии их взаимодействия:
A =W2 −W1 .
Имеем:
W1 = k q1rq1 2 ; W2 = k q1rq2 2 ;
Следовательно, |
|
|
|
|
|
|
|
|
A = k |
q1q2 |
−k |
q1q2 |
= kq q |
|
r1 −r2 |
=8 10−7 Дж. |
|
r |
r |
|
r r |
|||||
|
|
1 |
2 |
|
||||
2 |
1 |
|
|
1 |
2 |
|
||
Замечание. Работу A можно получить также, воспользовавшись тем, что работа внешних сил при перемещении заряда q1 в поле, созданном зарядом q2
равна
A = q |
(ϕ |
2 |
−ϕ ) , где ϕ |
= k q2 |
и ϕ |
2 |
= k q2 . |
|
1 |
|
1 |
1 |
r1 |
|
r2 |
||
|
|
|
|
|
|
|
||
Электроемкость. Конденсаторы. Энергия заряженных тел
Задание. Найти, с какой силой F притягиваются друг к другу пластины плоского заряженного конденсатора, емкость которого равна C , а разность потенциалов U . Расстояние между пластинами d .
Решение. Искомая сила равна
F = qE1 ,
где q =CU – заряд конденсатора (величина заряда на каждой из пластин), E1 – напряженность поля, создаваемого одной пластиной в месте нахождения второй
пластины. Для случая однородного электростатического поля E1 = 2Ud . Следова-
тельно,
F = CU2d 2 .
5
Постоянный электрический ток
Основные законы постоянного тока
Задание. Определить среднюю скорость υ направленного движения электронов вдоль медного проводника при плотности тока j=11А/мм2 . Считать, что на каждый атом меди в металле приходится один свободный электрон. Атомная масса меди µ =64г/моль, плотность меди D=8,9г/см3 .
Решение. Плотность тока j связана с величиной заряда электрона e, кон-
центрацией электронов n и средней скоростью их упорядоченного движения υ соотношением:
j=ne |
υ |
. |
(1) |
Действительно, по определению j=I/S, где S – площадь поперечного сечения проводника; I = ∆q / ∆t , где ∆q – заряд, прошедший через поперечное сече-
ние проводника за время ∆t . Далее очевидно, что ∆q = neV , где e – величина
заряда электрона, V = Sυ∆t – объем, в котором окажутся прошедшие через сечение проводника электроны за время ∆t . Из записанных выше соотношений получается уравнение (1).
Найдем концентрацию электронов в медном проводнике. Эта величина будет равна числу молей, содержащихся в единице объема, умноженному на
число Авогадро NA , т.е. |
D |
|
|
|
n = |
NA . |
(2) |
||
µ |
||||
|
|
|
Из (1) и (2) получим:
υ = µ j / (DNAe) ≈8 10−4 м/с.
Электромагнетизм
Магнитное поле в вакууме. Силы, действующие на токи и заряды в магнитном поле
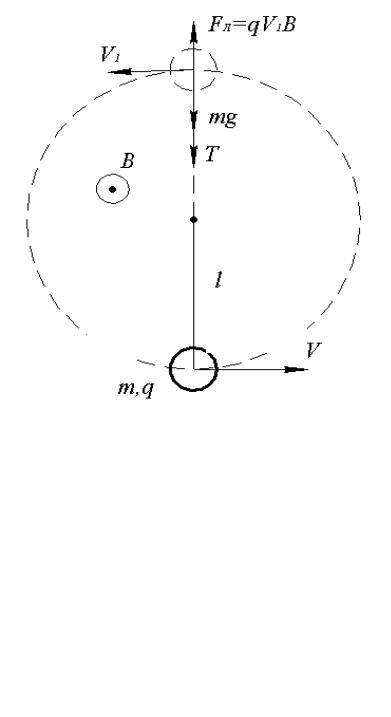
Задание. Небольшой шарик массой m заряжен положительным зарядом q , подвешен к легкой непроводящей и нерастяжимой нити длиной l и помещен
в однородное магнитное поле с индукцией B . Вектор B перпендикулярен плоскости, в которой может двигаться шарик (рис.1). Какую минимальную скорость надо сообщить шарику в горизонтальном направлении, чтобы шарик смог совершить полный оборот?
Решение. Пусть υ1 – скорость шарика в верхней точке траектории. Запи-
шем уравнение второго закона Ньютона для момента прохождения шариком этой точки:
6
|
mυ2 |
= mg + FН −qυ1B . |
(1) |
|
|
1 |
|||
l |
||||
|
|
|
||
Здесь FН – сила натяжения нити, qυ1B – сила Лоренца, mg |
– сила тяже- |
|||
сти.
Из закона сохранения и превращения механической энергии следует:
m2υ2 = m2υ12 + 2mgl ,
где |
mυ2 |
- кинетическая энергия шарика, сообщенная ему в горизонтальном на- |
|||||
2 |
|||||||
|
|
mυ2 |
|
|
|||
правлении; |
- то же в верхней точке траектории; 2mgl - потенциальная энер- |
||||||
1 |
|
||||||
2 |
|
||||||
|
|
|
|
|
|
||
гия шарика в верхней точке траектории. |
|
||||||
|
Отсюда υ2 |
=υ12 +4gl . |
(2) |
||||
|
Минимальная скорость υ , при которой шарик в верхней точке будет опи- |
||||||
сывать окружность, достигается при FН =0 .
Решая совместно уравнения (1) и (2) с учетом упомянутого условия, получим:
υ = 5gl + q2 B2l2 (1 − 1 + 4m2 g / q2 B2l) / 2m2 .
υ1 Fл = qυ1B
FН
υ
Рис.1
7
|
|
|
|
|
Электростатика |
||||
|
|
|
|
|
1.Электрический заряд |
||||
1.1. |
Металлическому шару путем удаления части электронов сообщается за- |
||||||||
ряд q=2Кл. На сколько |
|
∆M |
|
уменьшится масса шара? |
|||||
|
|
||||||||
1.2. |
Какую долю валентных электронов |
|
δN |
|
следует удалить с медного шари- |
||||
|
|
||||||||
ка объемом V=1см3 , чтобы получить на нем заряд q=1Кл? Валентность меди n=1. Молярная масса меди µ =64г/моль, плотность меди D=8,9г/см3.
2.Закон Кулона
2.1. На двух одинаковых капельках воды находится по одному избыточному электрону, причем сила электрического отталкивания капелек уравновешивает силу их гравитационного притяжения. Найдите радиусы r капелек. Плотность воды D=103 кг/м3 .
2.2. Два заряженных шарика, находящиеся на расстоянии r=0,6м, отталкиваются с силой F=0,3H. Суммарный заряд шариков q= – 8 10−6 Кл. Найдите заряды q1 и q 2 шариков.
2.3.Заряженные шарики, находящиеся на расстоянии r = 60см, притягиваются
с силой F=0,3Н. Суммарный заряд шариков q=4 10−6 Кл. Определите заряды q1 и q 2 шариков.
2.4.Три одинаковых точечных заряда q=3,46 10−6 Кл расположены в вершинах равностороннего треугольника. При помещении в центр треугольника точечного
заряда q1 результирующая сила, действующая на каждый заряд q, не изменяется по направлению, а по величине уменьшается в n=2 раза. Определите q1.
2.5.Два точечных заряда находятся на некотором расстоянии, их суммарный заряд равен q. Каковы эти заряды, если сила, действующая со стороны одного из них на другой максимальна по величине при данном q?
2.6. Два одинаковых проводящих шарика с зарядами q=2,4 10−9 Кл и q=9,6 10−9 Кл находятся на некотором расстоянии. Шарики приводят в соприкосновение и удаляют на прежнее расстояние. Найдите отношение F 2 /F1 вели-
чин сил взаимодействия шариков.
2.7. Два одинаковых проводящих шарика находятся на некотором расстоянии друг от друга. Заряд одного из них q1 = – 9 10−9 Кл, заряд другого q 2 =2 10−9 Кл.
Шарики привели в соприкосновение и вновь расположили на том же расстоянии. Как и во сколько раз изменилась при этом сила взаимодействия между шариками?
2.8. Четыре шарика массой m=2 10−3 кг каждый с одинаковыми зарядами q=2 10 −6 Кл удерживаются в вершинах квадрата со стороной L=0,02м. Определите величину a ускорения любого из шариков сразу после того, как их отпустят.
8

2.9. Одинаковые металлические шарики, находящиеся на некотором расстоянии, заряжены одноименными зарядами q1 и q 2 . Шарики привели в соприкос-
новение и удалили на прежнее расстояние. В результате сила отталкивания ша-
риков возросла в n=2 раза. Найдите отношение q1 . q2
2.10. Одинаковые металлические шарики с зарядами q1 и q 2 , находясь на неко-
тором расстоянии, притягиваются с некоторой силой. Если шарики привести в соприкосновение и удалить на прежнее расстояние, они будут отталкиваться с
силой в n=8 раз меньшей. Найдите отношение q1 . q2
2.11.Докажите, что если два одинаковых металлических шарика, заряженных одноименно неравными зарядами, привести в соприкосновение и затем раздвинуть на прежнее расстояние, то сила взаимодействия увеличится, причем приращение величины силы пропорционально квадрату разности зарядов.
2.12.Два одинаковых шарика подвешены на непроводящих нитях длиной l=2м
в одной точке. Когда каждому шарику сообщили заряд q=2 10−8 Кл, они разошлись на расстояние r=16см. Определите величину FН силы натяжения каждой нити.
2.13. Двум одинаковым проводящим шарикам сообщили заряды q1 и q 2 . Находясь на расстоянии r=0,2м, они притягиваются с силой F1 =4 10−3 Н. После того, как шарики были приведены в соприкосновение и возвращены в прежнее положение, они стали отталкиваться с силой F 2 =2,25 10−3 Н. Найдите q1 и q 2 .
2.14. Точечные заряды q1 =0,9 10−8 Кл, q 2 =10 −8 Кл, q 3 =6,4 10−8 Кл расположены на одной прямой, при этом расстояние между первым и вторым зарядами r1 =3 10−3 м, между вторым и третьим – r 2 =4 10−3 м. Найдите величину и направ-
ление результирующей силы F , с которой q1 и q 3 действуют на заряд q 2 .
2.15. Два одинаковых точечных заряда q=2 10−6 Кл находятся на расстоянии r=0,15м друг от друга. Какова величина F силы, с которой они действуют на точечный заряд q/ =6 10−6 Кл, находящийся на таком же расстоянии от каждого из них?
3.Напряженность электростатического поля системы точечных зарядов
3.1.Каков диаметр d масляной капли, которую с помощью одного избыточного электрона можно уравновесить в электрическом поле напряженностью Е=10
кВ/м? Плотность масла D=900кг/м3 .
3.2. Точечные заряды q1 =25нКл и q 2 = – 9нКл расположены на расстоянии l=6см. Найдите расстояние s от заряда q1 до точки, в которой напряженность электрического поля равна нулю.
9

3.3. Напряженность электрического поля точечного заряда в точке А равна ЕА =25В/м, а в точке В, лежащей на прямой, проходящей через заряд и точку А
составляет ЕВ =16В/м. Найдите величину ЕС напряженности электрического
поля в точке С – середине отрезка АВ. Точечный заряд не лежит на отрезке АВ. 3.4. В точке А находится точечный заряд. Точки В и С лежат на прямой, проходящей через точку А, по разные стороны от нее. Какова величина ЕD напря-
женности электростатического поля в точке D – середине отрезка ВС, если в точке В напряженность ЕВ =90В/м, в точке С – ЕС =10В/м?
3.5.Найдите величину Е напряженности электрического поля в вершине квадрата со стороной а=3м, если в три остальные вершины помещены точечные заряды q=2нКл.
3.6.В середине отрезка, на концах которого находятся точечные заряды q1 и
q 2 , величина напряженности электрического поля Е0 =7,2 10 3 В/м, а во всех равноудаленных от зарядов точках вектор напряженности электрического поля параллелен вектору Е0 . Расстояние между зарядами a=0,2м. Найдите q1 и q 2 .
3.7. В вершинах острых углов прямоугольного треугольника расположены точечные заряды q1 =2 10−9 и q 2 = – 2 10−9 Кл. Найдите величину Е напряженности электрического поля в вершине прямого угла. Длины катетов a=3см и d=4см.
3.8.Точечные заряды q=1 10−9 Кл расположены в трех вершинах прямоугольного треугольника с катетами а=40см и b=30см. Найдите величину Е напряженности электрического поля в точке пересечения гипотенузы с перпендикуляром, опущенным на нее из вершины прямого угла.
3.9.В двух вершинах правильного треугольника со стороной l=0,2м располо-
жены одинаковые точечные заряды q=9 10−10 Кл. Величина напряженности электрического поля в центре треугольника Е=300В/м. Определите диэлектрическую проницаемость ε среды, в которой находятся заряды.
3.10. Два точечных заряда, равных по величине и противоположных по знаку, закреплены на расстоянии l=2мм. Величина вектора напряженности электрического поля, созданного системой зарядов в точках, удаленных от каждого из них на расстояние d=1см, равна Е=2В/м. Найдите величину каждого заряда.
4. Напряженность электростатического поля протяженных заряженных тел
4.1.Две стороны равностороннего треугольника – однородно заряженные палочки. В центре треугольника величина напряженности электрического поля Е. Найдите напряженность электрического поля в центре треугольника после удаления одной из палочек.
4.2.По квадратной пластине со стороной а=20см равномерно распределен заряд q=35нКл. Оцените величины напряженностей электрического поля на перпендикуляре к квадрату, проходящему через его центр, в точках, отстоящих от квадрата на расстояния b=1см и с=15м.
10
