Учебное пособие 337

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ность применения формулы прямоугольников Rn

1.2. Формула трапеций

1.2. Формула трапеций

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

380.69 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Воронежский государственный архитектурно-строительный университет

Кафедра высшей математики

Приближенное вычисление определенных интегралов

Методические указания и задания по математике

Воронеж 2010

УДК 518.0 ББК 22.161я7

Составители Р. В. Чернышова, Н. А. Чернышов

Приближенное вычисление определенных интегралов: метод.

указания и задания по математике/ Воронежский гос. арх.-строит. ун-т; сост.: Р. В. Чернышова, Н. А. Чернышов. Воронеж, 2010. – 10 с.

Содержат 25 вариантов заданий по теме «Приближенное вычисление определенных интегралов». Приводятся примеры выполнения заданий.

Предназначены для студентов всех специальностей, кроме «ЭУН» и «Архитектура».

УДК 518.0 ББК 22.161я7

Печатается по решению редакционно-издательского совета Воронежского государственного архитектурно-строительного университета

Рецензент – М. Д. Гончаров, к. т. н., профессор кафедры высшей математики ВГАСУ

ВВЕДЕНИЕ

Данные методические указания предназначены для оказания помощи студентам в освоении численных методов интегрирования.

Изложено несколько способов приближенного интегрирования. Приведены примеры вычисления определенного интеграла различными

способами. Задания содержат 25 вариантов.

I. ЧИСЛЕННЫЕ МЕТОДЫ

При изучении неопределенных интегралов отмечалось, что всякая непрерывная на интервале (a, b) функция f (x) имеет первообразную, т. е. существует такая функция F (x), что F´(x)= f (x). В этом случае вычисление определенных интегралов осуществляется по формуле НьютонаЛейбница. Если же первообразная не выражается через элементарные функ-

ции (например,

и т. д.) то применяются различные ме-

тоды приближенного вычисления определенных интегралов, которые называются численными.

Суть их такова: площадь криволинейной трапеции (геометрический смысл определенного интеграла) заменяется другой, ограничивающая линия которой более простая, но мало отличается от заданной линии.

Рассмотрим несколько формул вычисления определенного интеграла

1.1. Формула прямоугольников

Пусть на отрезке 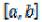задана непрерывная функция y=f (x). Разделим этот отрезок на n равных частей точками a=x0, x1, x2,… xn=b.

Длина каждого из отрезков равна h b n a . Значения функции в этих

точках обозначим y0, y1, y2…yn, yi=f (xi), i=0,1,…n

Заменим площадь криволинейной трапеции площадью ступенчатой фигуры, составленной из прямоугольников, высотами которых являются значения функции y0, y1, y2, …yn-1 как изображено на рис. 1. Тогда

b f (x)dx hy0 hy1 hy2 ... hyn 1 h( y0 y1

y2 ... yn 1 ) .

(1.1)

Если заменить площадь криволинейной трапеции площадью ступенчатой фигуры, составленной из прямоугольников, высотами которых являются значения функции y1, y2…yn, то

	b	f (x)dx hy1 hy2 ... hyn
	a
Рис. 1	h( y1 y2 ... yn ) .		(1.2)

Формула (1.1) позволяет вычислить определенный интеграл возрастающей функции с недостатком. Формула (1.2) – с избытком. Чем больше число n (т. е. чем меньше шаг деления h), тем меньше ошибка, совершаемая при вычислении интеграла по формулам (1.1) и (1.2). Формулы (1.1) и (1.2) называются формулами прямоугольников. Предельная абсолютная погреш-

Рис. 2

Разделим отрезок 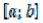на n равных частей длины h b n a точками

a = x0, x1, x2,…xn = b. Соответствующие ординаты этих точек графика функ-

ции обозначим y0, y1, y2 …yn, yi = f (xi) I = 0,1,2,…n.

Заменим кривую y=f (x) ломаной линией, звенья которой соединяют точки Аi, Аi-1 (i = 0,1,2,…n). В этом случае площадь криволинейной трапеции прибли-

женноравнасуммеплощадей соснованиямиyi-1, yi ивысотой h b n a (рис. 2):

f (x)dx

h ...

yn 1 yn

или

f ( x )dx

y 2

... y n 1

(2.1)

Формула (2.1) называется формулой трапеций. Предельная абсолютная погрешность вычисления по формуле трапеций:

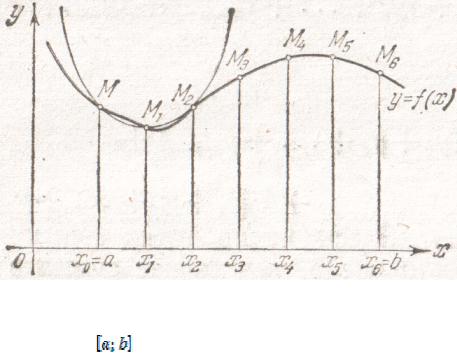
1.3. Формула парабол (Симпсона)

	Рис. 3		b a
Разделим отрезок	на 2n равных частей длиной	h		точками

x0 = a, x1, x2…x2n = b.			2n

Вычислимзначения функции y =f (x) в этих точках: y0, y1, y2 …y2n, yi =f (xi). Заменим дугу графика функции y = f (x) на каждом отрезке xi 1; xi 1 ду-

гой параболы, проходящей через точки (xi-1; yi-1), (xi; yi), (xi+1; yi+1), ось которой параллельна оси Oy (см. рис. 3). Тогда определенный интеграл будет

приближенно равен сумме площадей, заключенных под параболами:

b		y0	y2n 4 y1 y3 ... y2n 1 2 y2		... y2n 2 .
f (x)dx h		y0	y2n 4 y1 y3 ... y2n 1 2 y2	y4	... y2n 2 .	(3.1)
a	3

Формула (3.1) называется формулой парабол (или Симпсона). Предельная абсолютная погрешность вычисления по этой формуле:

R		h4		b a max	f IV (x)	.


n	180			[a,b]

II. РЕШЕНИЕ ТИПОВОГО ВАРИАНТА ЗАДАНИЯ
Пример 1. Вычислить 1	dx		, используя формулы (1.1), (1.2), (2.1),

0	1 x

(3.1), разделив отрезок на 10 частей. Вычисления вести с четырьмя верными знаками. Найти погрешность вычислений, полученных по приближенным формулам.

Решение. Вычислим сначала для сравнения этот интеграл по формуле Ньютона-Лейбница. Все вычисления проведем с одним запасным знаком:

1	dx	1	d(1 x)	ln	1 x	10	ln 2 ln1 ln 2 0,69315.


	1 x		1 x
0		0

ln2 вычислен по таблице.

Теперь найдем приближенное значение этого интеграла.

			Составим таблицу вычислений. Так как 2n = 10, то h																						1 0 0,1, yi			1	.
			Составим таблицу вычислений. Так как 2n = 10, то h																						1 0 0,1, yi				.
																									10			1 xi
																										Таблица 1

																				1						1
		i						xi									yi						i	xi		yi
		i						xi									yi	1 x					i	xi		yi	1 x
																				i							i
	0					0							1,00000									6		0,6		0,62500
	1					0,1							0,90909									7		0,7		0,58824
	2					0,2							0,83333									8		0,8		0,55556
	3					0,3							0,76923									9		0,9		0,52632
	4					0,4							0,71429									10		1,0		0,50000
	5					0,5							0,66667
			Вычислим интеграл, используя формулу (1.1):
				1	dx		h y			y		y					... y			0,1(1 0,90909 0,83333 0,76923 0,71429 0,66667
				0			h y		0	y		y				2	... y		9	0,1(1 0,90909 0,83333 0,76923 0,71429 0,66667
					1 x				0		1					2			9
					1 x
0,62500 0,58824 0,55556 0,52632) 0,1 7,18773 0,71877.
			Абсолютная ошибка этого приближенного значения равна
				0.69315 0.71877											0.02562.
				0.69315 0.71877											0.02562.
			Вычислим по формуле 1.2:
				1	dx		h y			y		... y 0,1(0,90909 0,83333 0,76923 0,71429 0,66667
				0			h y			y	2	... y 0,1(0,90909 0,83333 0,76923 0,71429 0,66667
					1 x			1			2						10
					1 x
				0,62500 0,58824 0,55556 0,52632 0,5) 0,1 6,68773 0,668773.
			Абсолютная ошибка приближенного значения равна
				0.69315 0.66877										0.02438.
				0.69315 0.66877										0.02438.
			Воспользуемся формулой трапеций (2.1):
	1 dx				y		0	y													1 0.5
				h			0	10		y		y					... y			0,1(			0.90909 0.83333 0.76923 0.71429
	0 1 x			h						y		y					... y			0,1(			0.90909 0.83333 0.76923 0.71429
	0 1 x							2			1					2			9		2

0.66667 0.62500 0.58824 0.55556 0.52632) 0.1 6.93773 0.69377 .

Абсолютная ошибка вычислений равна

0.69315 0.69377 0.00062.

Наконец вычисляем интеграл по формуле Симпсона (3.1):

1	dx	h	y		y	4( y y		y		y		y		2( y		y		y		y		))
0				0			3		5		7		9		2		4		6		8
	1 x 3				10	1

03,1 (1 0.5 4(0.90909 0.76923 0.66667 0.58824 0.52632) 2(0.83333 0.71429

0.62500 0.55556)) 0.69315.

Абсолютная погрешность равна

0.69315 0.69315 0.

Четвертая формула точнее остальных, так как абсолютная погрешность вычисления по этой формуле самая маленькая.

Пример 2. Вычислить 2 cos x dx, приняв n 6 , используя формулы пря-

0 1 x

моугольников, трапеций, Симпсона. Вычисления вести с пятью знаками после запятой. Оценить погрешность полученного результата.

Решение. Составим таблицу вычислений с одним запасным знаком;

h	b a			2			0			, 3.141593...., найдено по таблице;			yi	cos x	i .
h	n							12		, 3.141593...., найдено по таблице;			yi		i .
	n				6			12						1 xi
														Таблица 2

	i								xi			cosxi			cos xi
	i								xi		1 xi	cosxi			yi 1 x
															i
0		0									1	1		1
1					12						1,261799	0.965925		0,765514
					12
2					6						1,523582	0.866025		0,568414
					6
3						4					1,785373	0.707106		0,396055
						4
4					3						2,047198	0.500000		0,244236
					3
5			5 12								2,308997	0.258592		0.111993
6						2					2.5707965	0		0
						2

Вычислим определенный интеграл по формуле прямоугольников (1.1):

2 cos x dx

1 0.765514 0.568414 0.396055 0.244236 0.111993 0.261799 3.086212

1 x

0.807967.

Погрешность вычисления находим по формуле Rn

(b a) max

f '(x)

cos x '

[a,b]

sin x (1 x) cos x

sin x

cos x

;

Найдем f '(x)

1 x

(1 x)2

1 x

max

f '(x)

f '(0)

1, Rn

0.261799

0.205616 .

[0; ]

Следовательно, 2 cos x dx 0.807967 0.205616 , т. е. значение вычисляемо-

0 1 x

го интеграла находится в промежутке (0.807967-0.205616; 0.807967+0.205616).

Вычислим интеграл по формуле трапеций (2.1):

2 cos x

1 0

0 1 x dx

(

0.765514 0.568414 0.396055

0.244236 0.111993)

0.261799 2.586212 0.677067.

Погрешность вычисления найдем по формуле

(b a) max

f "(x)

[a,b]

f "(x)

cos x(1 x)2

2(sin x cos x sin x x)

cos x

2sin x

2 cos x

;

(1 x)3

1 x

(1 x)2

(1 x)3

max

f "(x)

f "(0)

[0,

]

(0.261799)2

1.570797

0.008972 .

0 1 0.005712

Следовательно, 2 cos x dx 0.677067 0.008972 , т. е. значение вычисляемого

0 1 x

интеграла находится в промежутке (0.677067-0.008972; 0.677067 + 0.008972).

Вычислим интеграл по формуле Симпсона (3.1):

				1 0.261799(1 0 4(0.765514 0.396055 0.111993) 2(0.568414 0.244236))
2 cos x dx
0	1 x			3
								0.087266(1 5.094248 1.625300) 0.673654.
	Rn				h4	(b a) max				f IV (x)			;
					h4
				180
				180				[a,b]
	f IV (x) cos x							4	sin x			12		cos x		24	sin x	24	cos x	;
	f IV (x) cos x							4	(1 x)2			12		(1 x)3		24	(1 x)4	24	(1 x)5	;
						1 x			(1 x)2					(1 x)3			(1 x)4		(1 x)5
	max		f IV (x)				13,		Rn		(0.261799)4				(	0) 13 0.000023252 1.5707965 0.000036.
											(0.261799)4

	[0,	]										180				2
	[0,	]										180				2
	2

Значит 2 cos x dx 0.673654 0.000036 . В качестве ответа надо взять зна-

0 1 x

чение интеграла, вычисленное по формуле Симпсона.

III. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

I. Вычислить b f (x)dx по формулам Ньютона-Лейбица, прямоугольни-

ков, трапеций, парабол. Вычисления проводить с точностью 0,0001. Найти абсолютную погрешность вычислений.

1.f (x) x x 1 , a = 4, b = 9, n = 10

2.f (x) 1 xx , a = 0, b = 1, n = 10

3.	f (x)			x	, a			= 3, b = 8, n = 10
3.	f (x)			1 x	, a			= 3, b = 8, n = 10
				1 x
4.	f (x)			x	, a			= 0, b = 1, n = 10
4.	f (x)	1		x	, a			= 0, b = 1, n = 10
		1		x
5.	f (x)			x2			, a = 0, b = 1, n = 10
5.	f (x)		(1 x2 )3				, a = 0, b = 1, n = 10
			(1 x2 )3
6.	f (x)			x2 1		, a = 1, b = 2, n = 10
6.	f (x)					, a = 1, b = 2, n = 10
				x
7.	f (x) (1 x2 )3 , a = 0, b = 1, n = 10
8.	f (x) x2 1 x2 , a = 0, b = 1, n = 10
9.	f (x)			1				, a = 0, b = 3, n = 10
9.	f (x)			(x2 3)5				, a = 0, b = 3, n = 10

10.f (x) ( 25x4 x2 )3 , a = 2,5, b = 5, n = 10

11.f (x) x e x , a = 0, b = 1, n = 10

12.f (x) xcox , a = 0, b = 2 , n = 10

13.f (x) sinx2 x , a = 6 , b = 3 , n = 10

14.f (x) x log2 x , a = 1, b = 2, n = 10

15.f (x) 1 cos1 x , a = 2 , b = 2 , n = 10

16.f (x) 3cossinxx , a = 6 , b = 2 , n = 6

17.f (x) cos2 x sin x , a = 0, b = 2 , n = 6

18.f (x) ctg3 x , a = 6 , b = 2 , n = 6

19.	f (x)	1			, a = 0 , b = 16 , n = 8
		x 9		x
20.	f (x)	1		, a = 13 , b = 2 , n = 10
		5 (3 x)4
21.	f (x)	1		, a = 1, b = 0 , n = 10
		1 3 1 x
22.	f (x) x2 9 x2 , a = 3 , b = 3 , n = 6
23.	f (x)	x	, a = 1, b = 5 , n = 8

		5 4x

24.f (x) 2 cos1 x , a = 0 , b = 2 , n = 6

25.f (x) 4 x2x 4 , a = 3 , b = 8 , n = 10

13.

11.

II. Вычислить приближенно, пользуясь формулами прямоугольников, трапеций, парабол, интеграл, который не может быть найден в конечном виде с помощьюэлементарныхфункций. Вычисленияпроводитьсточностью 0,0001.

1.	1	1 x3 dx , (n = 10)
	0
3.	1	1 x4 dx , (n = 10)
	0
5.	5	dx	, (n = 6)

	2 ln x
7.	3	cos d , (n = 10)

	0
9.	2	1 0,1sin2 d , (n = 6)

	0

3 sin xdx , (n = 10)

6 x

3 cos xdx , (n = 10)

6 x

2. 6 arctgx dx , (n = 10)

1 x

4. 33 sin xdx , (n = 10)

6.esin x dx , (n = 10)

8. 7 x2dx , (n = 10)

2 ln x

10. 6 ex dx , (n = 10)

1 x2

12. 1 3 x3 dx , (n = 10)


14. 2	2 cos d , (n = 10)
0

15.	1	ex	dx		, (n = 10)
15.	1	1 x	dx		, (n = 10)
	0	1 x
17.	2 e x2 dx , (n = 10)
	0
19.	2	1 x3 dx , (n = 10)
	0
21.	2	dx			, (n = 10)
21.	2	1 x		4	, (n = 10)
	0	1 x

2e x

23.x3 dx , (n = 10)


	16.	2	2 cos2 d , (n = 10)
		0

	18.	2sin xdx , (n = 10), (n = 10)
		0 1 x
	20.	2
	20.	3 1 0,5sin2 xdx , (n = 6)
		0
	22.	2	dx		, (n = 10)
	22.	2	3 x	3	, (n = 10)
		1	3 x
	24.	1	1 ex2 dx , (n = 10)
		0

25. 2	2 cos d , (n=10)
0

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022378.85 Кб5Учебное пособие 332.pdf
#
30.04.2022379.48 Кб2Учебное пособие 333.pdf
#
30.04.2022379.91 Кб2Учебное пособие 334.pdf
#
30.04.2022380.22 Кб4Учебное пособие 335.pdf
#
30.04.2022380.3 Кб1Учебное пособие 336.pdf
#
30.04.2022380.69 Кб3Учебное пособие 337.pdf
#
30.04.2022381.1 Кб3Учебное пособие 338.pdf
#
30.04.2022381.81 Кб3Учебное пособие 339.pdf
#
30.04.2022237.17 Кб1Учебное пособие 34.pdf
#
30.04.2022381.94 Кб3Учебное пособие 340.pdf
#
30.04.2022382.02 Кб4Учебное пособие 341.pdf