
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №12
Тема занятия: «Расчет переходных процессов методом интеграла Дюамеля»
Домашнее задание
Подготовиться к ответам на вопросы:
1.Дайте графическое и аналитическое представление для «единичного сигнала» и «единичного импульса».
2.Что такое переходная характеристика электрической
цепи?
3.Что такое импульсная характеристика цепи?
4.Какая существует связь между переходной и импульсной характеристиками?
5.Какая существует связь между операторным коэффициентом передачи цепи и изображением переходной характеристики?
6.Запишите основное выражение для интеграла Дюаме-
ля.
7.Как поступают, если входная функция воздействия при применении интеграла Дюамеля имеет различные выражения на разных интервалах времени?
8.Для каких типов четырёхполюсников применяется метод интеграла Дюамеля?
9.Почему в формуле интеграла Дюамеля аргументом переходной функции служит время, обозначаемое (t-τ)?
Основные положения и соотношения
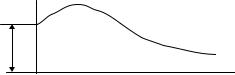
Если на пассивную цепь в момент t = 0 включается воздействие fг(t), являющееся непрерывной функцией времени
(рис. 12.1),
24
fr 
fr(0)
 t
t
Рис. 12.1
то реакцию цепи f(t) определяют интегралом Дюамеля по формуле
f (t)= fг (0) h(t) + ∫t |
fг′(τ) h (t −τ)dτ, |
|
|
(12.1) |
|
0 |
|
d fг (t) |
|
|
|
где fг(0) – начальное значение воздействия; fг′(τ)= |
|
- обо- |
|||
|
|||||
d t |
|||||
|
|
t=τ |
|||
|
|
|
|
||
значение производной воздействия, h(t-τ) – переходная характеристика цепи, в которой t заменено на t-τ.
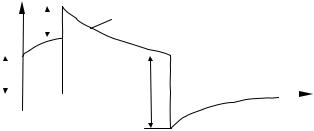
Если функция воздействия fг(t) имеет различные выражения на разных интервалах времени (рис. 11.2) и, кроме того, имеет или не имеет скачки, то интервал интегрирования разбивается на отдельные участки, а реакцию цепи, рассчитываемую интегралом Дюамеля, записывают для отдельных интервалов времени. В случае воздействия, изображённого на рис. 12.2, имеем
а) в первом интервале времени от 0 до t1 (не включая скачок F1)
f (t)= fг (0) h(t) + ∫t |
f1′(τ) h(t −τ)dτ, |
(12.2) |
0 |
|
|
25
|
fr |
|
|
|
|
|
|
|
|
|
|
F1 |
|
f2(t) |
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1(t) |
|
|
|
|
|
||
fr(0) |
|
F2 |
|
|
||||||
|
|
|
||||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
t |
|
0 |
|
t1 |
|
|
t1 |
|
||||
|
|
|
|
|
|
|
|
|
f3(t) |
|
Рис. 12.2
б) во втором интервале времени от t1 до t2 (не включая скачок F2)
t1 |
t |
|
f (t)= fг (0) h(t) + ∫f1′(τ) h (t −τ)dτ+F1h (t −t1 )+ ∫f2′ |
(τ) h (t −τ)dτ, (12.3) |
|
0 |
t1 |
|
здесь слагаемые F1h(t-t1) обусловлено положительным скачком воздействия в момент t1;
в) в третьем интервале времени от t2 до ∞
|
t |
|
|
f (t)= fг (0) h(t) + ∫1 f1′(τ) h (t −τ)dτ+F1h (t −t1 )+ |
|||
|
0 |
(12.4) |
|
t2 |
t |
||
|
|||
+ ∫f2′ |
(τ) h (t −τ)dτ−F2 h (t −t 2 )+ ∫f3′ |
(τ) h (t −τ)dτ, |
|
t1 |
t1 |
|
|
где слагаемое - F2h(t-t2) обусловлено отрицательным скачком воздействия в момент t2.
Входящие в формулы h(t-τ) есть h(t), в которых t заменено на t-τ.
26

Решить задачи
12.1.Для схемы, изображенной на рис. 12.3, определить переходную характеристику h(t), используя операторный метод.
12.2.Цепь, изображённая на рис. 12.3, включается на прямоугольный импульс напряжения U, действующий в течение
времени tu (рис. 12.4). Найти выражение напряжения на ёмкости uc(t) и токi (t) в зависимости от времени. Построить качественно кривые uc(t) и i(t).
u |
|
R |
|
e(t) |
|
C |
U |
0 |
tn |
t |
|
Рис. 12.3 |
Рис. 12.4 |
12.3. На входе линейной электрической цепи, переходная характеристика которой равна h(t) = e-t/а действует напряжение u1(t) = U0 + kt. Определить напряжение u2(t).
Примеры решения задач
12.4. Найти напряжение на выходе цепи (рис. 12.5), если напряжение на входных зажимах этой цепи изменяется во времени по закону
|
0 |
при |
t < 0 . |
|
u1 |
|
при |
0 |
≤ t < t . |
(t) = Ueat |
||||
|
0 |
при |
t |
≥ t1 . |
|
|
|
|
|
График входного напряжения u1(t) показан на рис. 12.6.
27
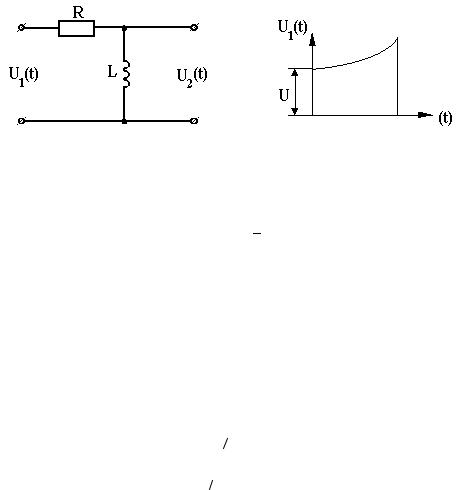
Рис. 12.5 |
Рис. 12.6 |
Переходная характеристика цепи (рис. 12.5) может быть определена в соответствии с примером 9.12, т.е.
−Rt
h(t) = e L .
При u1(t) в интервале времени |
0 ≤ t < t , воспользуемся |
|||||||||||||||||||
формулой интеграла Дюамеля (12.2), т.е. |
|
|
|
|
|
|
||||||||||||||
|
|
f (t)= f г (0) h(t) + ∫t f1′(τ) h(t −τ)dτ. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Подставляя соответствующие значения, получаем, что |
||||||||||||||||||||
u2 (t)= u1(0) h(t) + ∫t du1(τ) |
h(t − τ)dτ |
= |
|
|
|
|
|
|
||||||||||||
|
R |
|
t |
|
−aτ |
0 |
dτ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
}e−R(t−τ) Ldτ = |
|
|
|
|
|
|
|
|
|
||||||||
= Ue−L t |
+ ∫d{Ue |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0 |
dτ |
|
|
|
|
|
|
|
|
|
|
t |
|
(а+R )τ |
|
||
= Ue |
−R t |
+ |
t |
|
|
|
|
|
|
|
|
−R t |
+ Uаe |
−R t |
|
dτ = |
||||
L |
∫Uаeаτ e−R(t−τ) Ldτ = Ue |
|
L |
L |
∫e |
L |
|
|||||||||||||
|
|
|
0 |
R |
|
|
|
|
|
|
|
|
|
R |
0 |
|
|
|
||
|
|
|
|
|
|
|
(а+R )τ |
|
|
|
|
|
|
(а+R )t |
|
|
||||
= Ue |
−R t |
+ |
Uаe |
−L t |
e |
t |
= Ue |
−R t |
+ |
Uаe−L t |
e |
|
|
|||||||
L |
|
|
|
L |
|
L |
|
|
|
L |
−1 |
|||||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а + |
|
|
|
|
0 |
|
|
|
|
R |
|
|
|
|
|
||
|
|
|
L |
|
|
|
|
|
|
|
|
|
а + L |
|
|
|
|
|
||
В интервале времени при t > t1 получаем с учётом скачка в момент t1, что
28

|
|
|
t1 |
|
h(t −τ)dτ−u1 |
R |
u2 (t)= u1(0) h(t) + ∫du1(τ) |
(t1 )h(t −t1 )= Ue−L t |
|||||
|
R |
|
0 |
dτ |
|
|
+ |
Uаe− L t |
[e(а+R L)t1 |
−1]−Ue−аt1 e−R(t −t1) L. |
|
||
а +R L |
|
|||||
|
|
|
|
|
|
|
29
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Общая электротехника и электроника [Текст]: учеб. пособие. В 3 ч. Ч.2. Переходные процессы и спектры/ Б.В. Матвеев. - Воронеж: ГОУВПО «Воронежский государственный технический университет 2004. - 192 с.
2.Матвеев Б.В. Общая электротехника и электроника [Текст]: учеб. пособие/ Б.В. Матвеев. - Воронеж: ГОУВПО «Воронежский государственный технический университет,
2009. - 164 с.
СОДЕРЖАНИЕ
Практическое занятие № 9………………………………………1
Практическое занятие № 10……………………………………12
Практическое занятие №11…………………………………….17
Практическое занятие №12 ……………………………………24
Библиографический список……………………………………30
30
МЕТОДИЧЕСКОЕ РУКОВОДСТВО
к практическим занятиям № 9-12 по теме «Переходные процессы в линейных цепях»
по дисциплине «Электротехника и электроника» для студентов направления подготовки
11.03.03 «Конструирование и технология электронных средств» (направленность «Проектирование и технология радиоэлектронных средств») очной формы обучения
Составители: Матвеев Борис Васильевич, Поветко Василий Николаевич, Малышев Иван Иосифович
В авторской редакции
Подписано в печать 23.10.2017.
Формат 60х 84/16. Бумага для множительных аппаратов. Усл. печ. л. 2,1. Уч. изд. л. 1,9. Тираж 34 экз. «С» 25.
Зак. № 139.
ФГБОУ ВО «Воронежский государственный технический университет»
394026 Воронеж, Московский просп., 14
Участок оперативной полиграфии издательства ВГТУ 394026 Воронеж, Московский просп., 14
31
