
Одномерная оптимизация функций. методические указания по курсу «Информатика» для студентов II курса всех специальностей. Гильмутдинов В.И., Кононов А.Д
.pdfФедеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Воронежский государственный архитектурно-строительный университет
Кафедра математического моделирования и вычислительной техники
Одномерная оптимизация функций
Методические указания по курсу «Информатика» для студентов
II курса всех специальностей
Воронеж 2009
Составители В.И. Гильмутдинов, А.Д. Кононов, А.А. Кононов
УДК 69.003:658.5.012.22
ББК 32.973
Одномерная оптимизация функций: метод. указания по курсу «Инфор-
матика» для студ. II курса всех спец. / Воронеж. гос. арх.-строит. ун-т; сост.: В.И. Гильмутдинов, А.Д. Кононов, А.А. Кононов. –Воронеж, 2009. – 16 с.
Рассматриваются методы решения задач оптимизации, лежащие в основе машинного управления и проектирования. Предлагаются задания для выполнения соответствующих разделов лабораторного практикума. Методические указания предназначены для использования на лабораторных, а также индивидуальных занятиях при изучении дисциплины «Информатика» студентами второго курса всех специальностей.
Табл. 1. Ил. 9. Библиог.: 3 назв.
Печатается по решению редакционно-издательского совета Воронежского государственного архитектурно-строительного университета
Рецензент – В.К. Маршаков, к. ф.–м. н., доц. Воронежского государственного университета
3
ВВЕДЕНИЕ
Экономическое планирование, проектирование сооружений и многие другие виды творческой деятельности специалистов связаны с поиском рационального решения поставленной задачи. При этом оптимальным называют наилучший в определенном смысле вариант подбора проектных параметров. Через проектные параметры выражается целевая функция, для которой требуется найти экстремальное (минимальное или максимальное) значение.
В общем случае целевая функция f(x) может иметь несколько экстремумов. Из них главный (оптимальное решение для пространства проектирования) называется глобальным. Задача поиска экстремумов сводится к их локализации и уточнению значений x и f(x) в точке экстремума. В дальнейшем для функции одной переменной под экстремумом будем подразумевать минимум функции f(x). Поскольку минимуму функции f(x) соответствует максимум функции –f(x), то, сменив знак у f(x), программами поиска минимума можно пользоваться и для поиска максимума функций.
Минимизация функции одной переменной представляет самостоятельный интерес и является важным элементом различных процедур минимизации функций нескольких переменных. От правильной организации одномерного поиска существенно зависит успех решения всей задачи.
1. Прямые методы оптимизации
Большую группу приближенных методов минимизации функций составляют прямые методы минимизации, основанные на вычислении только значений минимизируемой функции в некоторых точках и не использующие значений ее производных.
Пусть f(x) – функция, определенная на отрезке [a,b]. Функцию f(x) называют унимодальной, если существует единственная точка x*, в которой f(x) принимает экстремальное значение. Для определенности будем считать, что речь идет о минимуме функции f(x) на отрезке [a,b]. Из определения унимодальности следует, что если x1<x2£ x*, то f(x1)>f(x2). Аналогично, если x*£x1<x2, то f(x1)<f(x2). Множество функций, унимодальных на отрезке [a,b], будем обозначать Q[a,b]. Отметим, что в инженерной практике обычно встречаются именно такие целевые функции.
1.1. Метод равномерного поиска. Этот метод, рассмотренный в [1], основан на том, что переменной x присваиваются значения x + Dx с постоянным шагом, и вычисляются последовательные значения f(x). Если f (xn+1 )< f (xn )
переменной x дается очередное приращение. Как только f (xn+1 ) станет больше f (xn ), поиск останавливается. При малой заданной погрешности метод равно-
мерного поиска неэкономичен по затратам машинного времени.
1.2. Метод поразрядного приближения. Является усовершенствованием
4
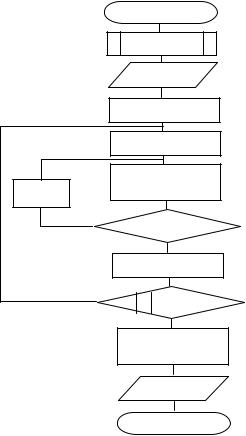
метода равномерного поиска, в котором шаг и направление поиска не являются постоянными. Метод поразрядного поиска реализуется следующим алгоритмом
(рис. 1).
Исходными данными для алгоритма являются:
x0 – начальное приближение слева от минимума функции f(x), описанной в подпрограмме (блок 1);
h – начальный шаг поиска;
e – заданная погрешность вычисления x* в точке минимума.
По структуре алгоритм представляет собой многоступенчатый циклический процесс итерационного типа. Во внутреннем цикле (блоки 5 – 7) путем обращения к подпрограмме (блок 1) вычисляются значения функции f(x) в точках x, отстоящих на величину шага (блок 4), и соседние значения поочередно
сравниваются друг с другом. Если условие f (xn+1 )< f (xn ), (n – номер шага),
записанное в блоке 6, выполняется, то происходит дальнейшее перемещение точки поиска внутри отрезка [а, b]. Если условие не выполняется, то цикл (блоки 5 – 7) завершается и выбирается новое значение шага h = – h/4 (блок 8), чем обеспечивается поиск минимума в другом направлении с шагом в 4 раза меньше прежнего.
|
|
начало |
||
|
1 |
f ( x ) = ... |
||
|
2 |
x 0 , h ,e |
||
|
3 |
x = x 0 |
||
|
|
|||
|
4 G |
= f ( x ) |
||
7 |
5 |
x = x + h |
||
|
R |
= |
f ( x ) |
|
G = R |
|
|||
|
|
|
|
|
да |
6 |
R < G |
||
|
||||
|
|
|
|
нет |
|
8 h = - h / 4 |
|||
да |
9 |
h |
> e / 4 |
|
|
||||
|
10 x |
|
нет |
|
|
* |
= x |
||
|
|
f * |
= |
f ( x* ) |
|
|
11 |
x * , f * |
|
|
|
|
конец |
|
Рис. 1. Блок-схема алгоритма поиска минимума функций f(x) методом поразрядного приближения
5
Во внешнем цикле (блоки 4 – 9) осуществляется следующий этап уточнения определения минимума функции и контроль требуемой точности, при достижении которой происходит выход из цикла (блоки 4 – 9), вычисление искомых параметров (блок 10) и вывод результатов решения задачи x*, f* (блок 11).
Наглядность алгоритма можно повысить, перенеся блок вывода значений x*, f* внутрь цикла (блоки 4 – 9), что позволит наблюдать динамику поиска экстремума функции.
Процесс решения задачи оптимизации рассматриваемыми ниже методами состоит в последовательном сужении интервала изменения проектного параметра x, называемого интервалом неопределенности. В начале процесса оптимизации его длина равна b-a, а к концу, после выполнения n шагов, она должна стать менее заданного допустимого значения e >0, определяющего точность вычислений, при этом оптимальное значение проектного параметра x* должно находиться в интервале неопределенности – отрезке [xn, xn+1].
1.3. Метод деления отрезка пополам. Пусть функция f(x)ÎQ[a,b], тре-
буется найти x* – точку минимума функции f(x) на отрезке [a,b] с заданной погрешностью e >0. Выберем некоторую достаточно малую величину dÎ(0, 2e), и
разделим отрезок [a,b] двумя точками |
|
|
x1 =(a+b-d)/2, |
x2 =(a+b+d)/2. |
(1) |
Очевидно, что x1 <x2. Согласно вышесказанному для продолжения процесса деления необходимо выбрать такой отрезок [a1,b1], чтобы он содержал точку x* и был меньше исходного отрезка [a,b]. Тогда выбираем
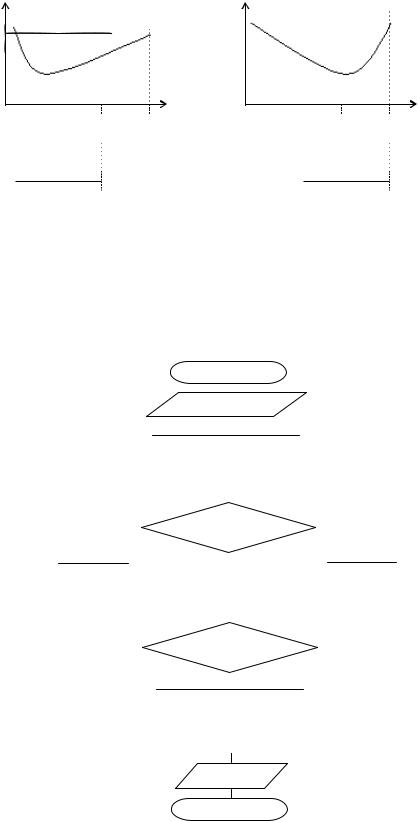
a1 =a, b1 =x2, если f(x1) ≤ f(x2),
поскольку, как следует из условия унимодальности функции f(x), точка минимума x* в этом случае лежит слева от точки x2 (рис. 2а)) и
a1 =x1, b1 =b, если f(x1) >f(x2) (рис. 2б)).
Вышеописанную процедуру деления повторяют до тех пор, пока на n -ом шаге мы не получим, что
|bn - an | £ e
итогда за приближенное значение точки минимума с точностью e выбирают
середину отрезка, полученного после n - кратного деления |
|
x* »( an +bn ) / 2. |
(2) |
Точность вычисления при этом не превосходит величину |
|
e £ ( bn - an ) / 2 . |
(3) |
Из последнего выражения можно найти необходимое число шагов n |
для |
обеспечения заданной точности вычислений. |
|
Для увеличения скорости сходимости метода величину dÎ(0,2e) целесообразно выбирать как можно меньшей, однако этот выбор ограничен снизу используемым количеством верных десятичных знаков при задании аргумента x. В любом случае d должно быть больше машинного нуля применяемого вычислительного средства.
6
f(x) |
f(x) |
|
|
x |
|
|
x |
a x* x1 |
x2 |
b |
a |
x1 |
x2 x* b |
a1 x* |
b1 |
a1 |
x* |
b1 |
|
а) |
|
б) |
|
Рис. 2. Уменьшение интервала неопределенности а) минимум слева; б) минимум справа
Блок-схема алгоритма метода деления отрезка пополам [2] представлена на рис. 3.
|
|
|
|
|
|
|
начало |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
1 a ,b , |
|
e ,d |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x1 =(a+b-d)/2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x2 =(a+b+d)/2 |
|
|
|
|
|
|
|
|
|||||
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
f(x1 |
) £ f(x 2 ) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
= x1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
b = x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
6 (b-a) / 2£ e |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
7 |
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x* = ( a + b ) / 2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
f * |
= f ( x* ) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8
f * , x *
конец
Рис. 3. Блок-схема алгоритма метода деления отрезка пополам

7
1.4. Метод золотого сечения. При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений (или измерений – при проведении эксперимента) значений целевой функции f(x). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения. Опираясь на свойство золотого сечения отрезка, он использует найденные значения f(x) более рационально, чем метод деления отрезка пополам. Это позволяет переходить к очередному отрезку, содержащему точку x*, после вычисления одного, а не двух значений f(x).
Деление отрезка на две неравные части так, что отношение длины всего отрезка к длине большей его части равно отношению длины большей части к длине меньшей части, называется золотым сечением этого отрезка. Нетрудно проверить, что золотое сечение отрезка [a, b] производят две симметрично расположенные точки:
x1= a+(1-t)(b-a), x2 =a+t(b-a), где t =( 
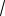 5 - 1 )/2 = 0.6180339. (4)
5 - 1 )/2 = 0.6180339. (4)
Отметим, что точка x1, в свою очередь, производит золотое сечение отрезка [a, x2] (вторая точка), а точка x2 – золотое сечение отрезка [x1, b] (первая точка). Зная одну из точек золотого сечения отрезка [a, b], другую можно найти по одной из формул
x1 = a+b-x2, |
x2 = a+b-x1. |
(5) |
Пусть f(x)ÎQ[a, b] и требуется найти точку минимума x* функции |
f(x) на |
|
[a, b]. Опишем алгоритм поиска. Начальный отрезок делим точками x1 |
и x2 по |
|
правилу золотого сечения и в указанных точках вычисляем значения функций f(x1) и f(x2). Если f(x1) £ f(x2), то для дальнейшего поиска оставляем отрезок [a, x2], так как, согласно свойству унимодальности, именно он содержит точку x*; если f(x1) > f(x2) – то отрезок [x1, b]. Поскольку на оставшемся отрезке уже есть одна точка, производящая золотое сечение, находим вторую точку. После этого процесс повторяем до тех пор, пока на n-м шаге интервал неопределенности не станет меньше заданной точности e. Тогда за приближенное значение точки минимума x* с точностью e выбирают точку золотого сечения, содержащуюся на последнем полученном отрезке.
Следовательно, алгоритм поиска сводится к нахождению последовательностей {an}, {bn} и {xn}, при n = 1,2, ... , определяемых соотношениями:
an= an-1, |
bn= x2(n-1), |
xn = x1(n-1), |
если |
f(x1(n-1)) £ f(x2(n-1)); |
an=x1(n-1), bn=bn-1, |
xn = x2(n-1), |
если |
f(x1(n-1)) > f(x2(n-1)), n = 2,3,...., (6) |
|
где а1=a, b1=b, |
x1(n-1) и x2(n-1) – первая и вторая точки золотого сечения отрез- |
|||
ка [an-1, bn-1]. |
|
|
|
|
Таким образом, на каждом шаге, начиная со второго, требуется лишь одно вычисление функции, и интервал неопределенности становится равным
0.618 от предыдущего. Положив x* » xn, найдем точку минимума x* с точностью en:
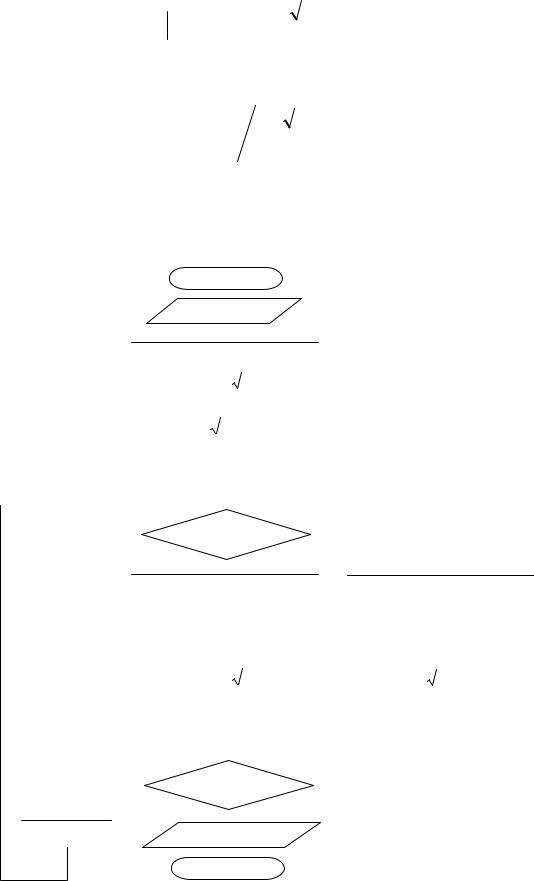
8
|
|
|
|
æ |
|
|
-1 |
ön |
|
|
|
|
|
|
5 |
|
|
||||
|
|
|
|
|
|
|||||
x* - x |
n |
£ e |
n |
= ç |
|
|
|
÷ |
( b - a ) |
, |
|
|
|
||||||||
|
|
ç |
|
2 |
÷ |
|
||||
|
|
|
|
è |
|
ø |
|
|
||
откуда следует, что число шагов n метода золотого сечения, обеспечивающее заданную точность e нахождения точки x*, должно удовлетворять неравенству
æ |
e |
ö |
æ |
|
|
- 1 |
ö |
æ b - a ö |
|
|
||
5 |
|
|
||||||||||
n ³ ln ç |
|
÷ |
lnç |
|
|
|
÷ |
» 2.1 lnç |
|
÷ |
. |
(7) |
|
|
|
|
|
||||||||
è b - a ø |
ç |
|
2 |
÷ |
è |
e |
ø |
|||||
è |
|
ø |
|
|
||||||||
При определении x* с большой точностью, чтобы избежать накопления ошибок округления, обычно точки золотого сечения отрезка [an, bn] находят по формулам (4). В этом случае блок-схема алгоритма метода золотого сечения [3] имеет вид, представленный на рис. 4.
начало
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a ,b ,e |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
n =1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
3 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x1 |
= a + |
5 |
|
(b - a) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
- 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x2 |
= a + |
5 |
|
|
(b - a) |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
f1 = f (x1 ) f 2 = f (x2 ) |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|||
|
3 |
|
|
|
f1 £ f 2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
5 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
x = x1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x = x2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b=x2 |
|
|
|
a=x1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
x2 = x |
|
|
|
x1 |
= x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
f2 = f1 |
|
|
|
f1 = f2 |
|
|||||||||||||||
|
|
|
|
|
x1 |
= a + |
|
|
|
3 - |
5 |
|
(b - a) |
|
|
x2 = a + |
|
5 |
- 1 |
(b - a) |
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
f1 = f (x1 ) |
|
|
f 2 = f (x2 ) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
b - a |
|
< e |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
7n = |
|
|
|
|
|
|
8x , f ( |
|
|
|
да |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
n + 1 |
|
|
|
|
|
|
x ),e , n |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
конец
Рис. 4. Блок-схема алгоритма метода золотого сечения

9
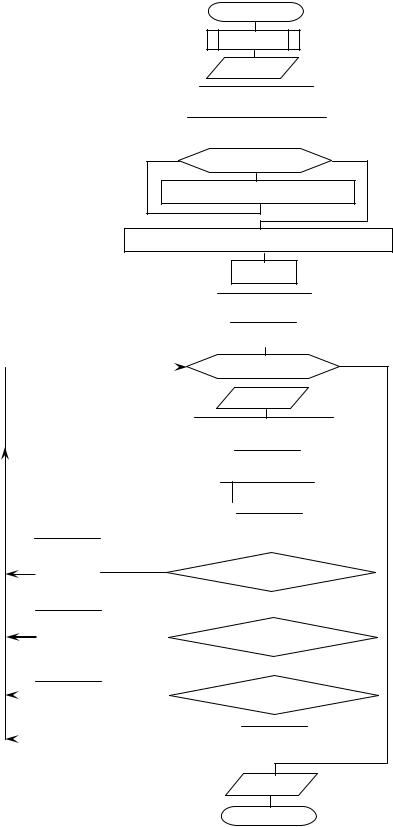
1.5. Метод Фибоначчи. Метод Фибоначчи, как и метод золотого сечения, основан на делении и последующем сужении исходного интервала неопределенности. При применении метода Фибоначчи для этого используются так называемые числа Фибоначчи, где новое число равно сумме двух предыдущих.
Блок-схема алгоритма поиска минимума одномерной функции с помощью чисел Фибоначчи представлена на рис. 5.
Исходными данными для алгоритма являются:
a и b – границы интервала поиска экстремума функции f(x);
N – задаваемая пользователем длина последовательности чисел Фибонач-
чи.
По структуре алгоритм представляет собой циклический вычислительный процесс. В блоке 4 задаются первые два числа Фибоначчи. Цикл (блоки 5, 6) вычисляет числа Фибоначчи и размещает их в массиве D. Эти числа используются в блоках 7 – 10 для вычисления x, а затем с помощью обращения к подпрограмме (блок 1) значения y. В цикле (блоки 11 – 23) проверяются соответствующие условия (блоки 17, 19, 21) и происходит сужение интервала неопределенности. Блок 24 выводит результат решения задачи.
Алгоритм, представленный на рис. 5, легко может быть преобразован в итерационный вычислительный процесс, проверяющий достижение заданной погрешности вычислений с проверкой достижения точности с помощью анали-
за условия x1 - x3 < e .
1.6.Метод квадратичной интерполяции – экстраполяции заключается
взамене функции f(x) в промежутке x1 ± h , где x1 – начальное приближение,
квадратичной параболой, экстремум которой вычисляется аналитически. После нахождения экстремума x* (максимума или минимума) можно задать x1 = x* и повторить поиск.
Таким образом, с помощью итерационной процедуры значение x* уточняется до получения его с заданной погрешностью e. Этот метод обеспечивает поиск как минимумов, так и максимумов f(x), причем точка x* может лежать в интервале x1 ± h (интерполяция) и быть вне его (экстраполяция).
Блок-схема алгоритма вычисления экстремумов функции одной переменной методом квадратичной интерполяции – экстраполяции приведена на рис. 6.
Исходными данными для алгоритма являются: x1 – начальное приближение;
h – шаг (полуинтервал интерполяции – экстраполяции); e – заданная погрешность результата.
В блоке 3 путем обращения к подпрограмме (блок 1) вычисляются три значения функции f(x) в смежных значениях аргумента f0=f(x1-h); f1=f(x1); f2=f(x1+h) и для параболы, проходящей через выбранные узлы интерполяции – экстраполяции, находится положение экстремума (блок 4).
10
начало
|
18 |
= x 2 |
|
|
|
x 3 |
|
|
|
|
x 2 |
= x 4 |
|
|
|
y 2 |
= y 4 |
|
|
|
|
|
|
|
|
20 |
= x 2 |
|
|
|
x1 |
|
||
|
x 2 |
= x 4 |
|
|
|
y 2 |
= y1 |
|
|
|
|
|
|
|
|
22 |
= x 4 |
|
|
|
x1 |
|
||
1 f ( x ) = ...
2
a , b , N
4 |
|
3x1 = a |
|
|
x3 = b |
|
|
|
|
|
|
||||
|
|
|
|
D (1) = 1 |
|
||
D ( 0 ) = 1 |
|
|
|||||
5 |
|
|
|
|
|
||
|
|
|
|
||||
i = 2 , N
6
D (i ) = D (i - 1) + D (i - 2 )
7
x2 = x1 + ( x3 - x1 ) * D( N - 1 ) / D( N )
8x = x 2
|
|
|
9 |
|
|
|
|
y = |
|
f ( x ) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10y 2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
= y |
|
|
|
|
|
||||||||
|
|
|
11 i = 1, N |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x1 , x 3 |
||||||||||
|
|
13x 4 = x1 - |
x 2 + x 3 |
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x = x 4 |
|
|
|
|
||||||
|
|
|
|
|
15 |
|
y = |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
f ( x ) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 4 |
|
= y |
|
|
||||||
да |
|
x |
17 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 > x 4 и y 2 > y 4 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
да |
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y 2 |
|
> y 4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
да |
|
|
21 |
|
|
|
|
|
нет |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x 2 |
|
> x 4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
нет |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x 3 = x 4 |
|
|||||||||
24 y 2
конец
Рис. 5. Блок-схема алгоритма поиска минимума одномерной функции с помощью чисел Фибоначчи
