
Учебное пособие 69
.pdf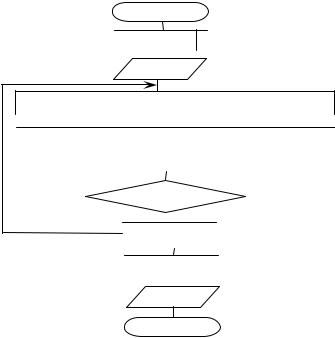
|
|
|
|
11 |
В блоке |
5 анализируется достижение заданной точности. Если условие |
|||
|
x* - x1 |
|
< e |
не выполняется, задаем x1 = x* (блок 6) и уточнение продолжается. |
|
|
|||
В противном случае x* считается найденным с заданной погрешностью e, в блоке 7 вычисляется значение f(x*) и выводятся результаты решения задачи
(блок 8).
начало
|
1 |
|
f |
( x ) = ... |
|
|||
|
|
|
||||||
|
|
|
|
|
|
|
||
2 |
|
|
|
|||||
, h ,e |
||||||||
|
|
|
x |
1 |
||||
3f 0 = f ( x1 - h ), f 1 = f ( x1 ), f 2 = f ( x1 + h )
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
f 0 ( 2 x 1 |
+ h ) |
- 4 f 1 × x 1 + f 2 ( 2 x 1 - h ) |
|||||||||||
|
x * = |
× |
||||||||||||||
|
|
2 |
|
|
|
|
|
|
f 0 - 2 f 1 |
+ f 2 |
||||||
|
|
|
|
5 |
|
x * |
- x 1 |
|
< e |
да |
|
|
||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
6 |
|
|
|
|
нет |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x 1 |
= x * |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
7 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( x * ) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
f * |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
8x * |
|
|
|
|
|
||||
|
|
|
|
|
|
|
, f * |
|
|
|
||||||
конец
Рис. 6. Блок-схема алгоритма вычисления экстремумов функции одной переменной методом квадратичной интерполяции – экстраполяции
2. Методы минимизации, основанные на использовании производных функции
Если вычисление или измерение производных функции f(x) не представляет больших затруднений, то при решении задачи минимизации можно применять непрямые методы, основанные на использовании производных f(x). Во многих случаях эти методы обеспечивают более быструю сходимость, чем прямые методы минимизации.
2.1. Метод касательных применяется для минимизации выпуклых дифференцируемых функций. Функция f(x) называется выпуклой на отрезке [a, b], если
f [a x1 + (1-a ) x2] £ a f(x1) + (1-a ) f(x2) |
(8) |
для произвольных x1, x2 Î[a,b] и a Î[0,1]. |
|
Проверка условия (8) почти всегда вызывает затруднения, |
поэтому на |
12
практике используют следующий критерий выпуклости:
Для того, чтобы дважды дифференцируемая на отрезке [a, b] функция f(x) была выпуклой на этом отрезке, необходимо и достаточно, чтобы f² (x) ³ 0 при всех xÎ[a, b].
Опишем метод касательных. Пусть f(x) – выпуклая дифференцируемая на отрезке [a, b] функция, причем f¢(a)· f¢(b) < 0. Построим последовательности {an}, {bn} и {сn}, при n = 1,2, ... в соответствии с рекуррентными соотношения-
ми |
|
|
|
|
bn-1 f ¢(bn-1 )- an-1 |
f ¢(an-1 )+ f (an-1 )- f (bn-1 ) |
|
|
||
a |
0 |
= a, b = b, c |
n-1 |
= |
, |
(9) |
||||
|
|
|||||||||
|
0 |
|
|
f ¢(bn-1 )- f ¢(an-1 ) |
||||||
|
|
|
|
|
|
|
|
|||
|
|
an = an-1 , |
bn |
= cn-1 |
при |
f ¢(cn-1 )³ 0 , |
|
|
||
|
|
an = cn-1 , |
bn |
= bn-1 |
при |
f ¢(cn-1 )< 0 . |
|
(10) |
||
После n шагов полагаем x* » cn, |
f* » f(cn). Требуемая точность минимиза- |
|||||||||
ции f(x) считается достигнутой, если производная f¢(cn) достаточно близка к нулю, то есть f ¢(cn ) £ e , где ε > 0 – заданное число, характеризующее точность.
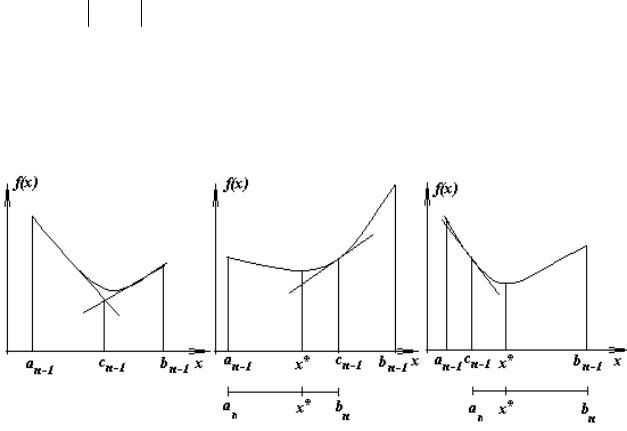
Метод касательных имеет простой геометрический смысл: величина cn-1 из (9) – это абсцисса точки пересечения касательных к графику f(x), проведенных в граничных точках отрезка [an-1, bn-1] (рис. 7а)). Рис. 7б) и рис. 7в) поясняют формулы (9) для случаев f¢(cn-1) > 0 и f¢(cn-1) < 0 соответственно. Отрезок [an, bn] выбирается так, чтобы x* Î[an, bn].
а) |
б) |
в) |
Рис. 7. Геометрический смысл метода касательных а) пересечение касательных, проведенных в граничных точках;
б) f¢(cn-1) > 0; в) f¢(cn-1) < 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Если условие f¢(a) · f¢(b) < 0 не выполняется, то |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
а) x* = a |
при f¢(a) > 0, |
|
f¢(b) > 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
б) x* = b |
при f¢(a) < 0, |
|
f¢(b) < 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
в) x* = a, |
если f¢(a) = 0, и x* = b, если f¢(b) = 0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
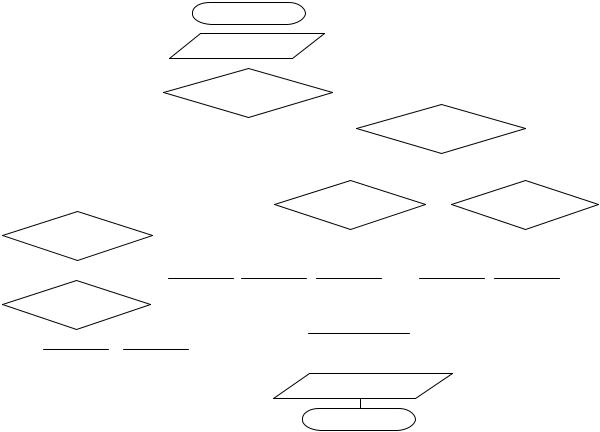
Блок-схема алгоритма метода касательных представлена на рис. 8. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
начало |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a ,b ,e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
да |
2 |
|
|
¢ |
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (a)f |
(b)< 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
9 |
|
f |
¢ |
|
|
¢ |
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
¢ |
|
|
|
¢ |
|
|
|
|
|
(a)- f (b) |
|
|
|
|
|
|
|
|
|
|
|
(a)f |
(b)> 0 |
|
нет |
||||||||||||||||||||
|
|
c = |
|
b × f (b)- a × f (a)+ f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
f |
¢ |
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
(a)- f |
(b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
f |
(a)> 0 |
|
|
|
|
|
|
11 |
|
f (a)= 0 |
||||||
|
|
|
|
¢ |
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
|
|
f |
|
(c |
|
) |
£ e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
да |
|
нет |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
8 |
|
= c |
|
12 |
|
|
|
|
|
13 |
|
|
|
|
|
|
|
14 |
|
|
|
|
15 |
= b |
|
||||||||
|
|
|
f |
¢ |
|
|
|
|
|
|
нет |
|
x* |
|
|
|
x* = a |
|
|
x* = b |
|
|
|
|
x* = a |
|
x* |
|
|||||||||||||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
(x*) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
6 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f * = f |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
a = c |
|
|
b = c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f *, x * |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
конец
Рис. 8. Блок-схема алгоритма метода касательных
2.2. Метод Ньютона, использующий не только первую, но и вторую производные функции f(x), при определенных условиях обеспечивает значительно более высокую, чем рассмотренные ранее методы минимизации скорость сходимости к точке минимума x*.
Пусть f(x) – выпуклая, дважды дифференцируемая функция. Выбрав на-
чальное приближение x0, построим последовательность |
|
|
xn = xn-1 - f¢(xn-1)/f²(xn-1), |
n = 1,2,... |
(11) |
Считая неравенство | f¢(xn) | £ e ( e – достаточно малое число) условием
достижения требуемой точности вычислений, положим x* » xn, f* » f(xn).
При неудачном выборе x0 последовательность (11) может расходиться. Если же точка x0 достаточно близка к x*, то эта последовательность сходится к x* достаточно быстро.
Оценка скорости сходимости может быть определена следующим образом. Пусть f(x) – дважды дифференцируемая функция, причем f² (x)³ m > 0 и f²(x)
14
удовлетворяет условию Липшица с константой L. Тогда, если начальное при-
ближение x0 удовлетворяет условию
q =L | f¢(x0)| / (2m2) < 1,
то последовательность (11) сходится к единственной точке минимума x* функции f(x), причем
| x* - xn | £ 2m q2n/ L, |
n = 0,1,... |
Метод Ньютона часто используется на завершающем этапе минимизации, когда точка минимума x* грубо найдена другим, менее трудоемким методом и требуется найти x* с большей точностью.
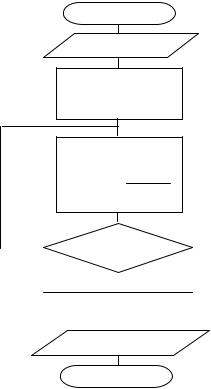
Блок-схема алгоритма метода Ньютона представлена на рис. 9.
начало
1a ,b , x0 ,e
2n = 0
x= x0
3n = n + 1
=- f ¢(x)
xx
f ¢¢(x)
нет |
|
4 |
|
f |
(x) |
|
< e |
|
|
|
|
||||||
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
f * |
= f (x) |
|||||
|
|
|
||||||
|
|
6 |
|
x , f *, n |
||||
|
|
|
|
|||||
конец
Рис. 9. Блок-схема алгоритма метода Ньютона
3. Задание
Набор задач и методов оптимизации, выполняемых в рамках лабораторного практикума и на индивидуальных занятиях, определяется для каждой специальности преподавателем в соответствии с объемом дисциплины «Информатика» и специализации обучаемых.
1) С помощью различных методов, приведенных в данных методических указаниях, решить задачу минимизации унимодальной функции f(x) на отрезке [a, b] (таблица) для варианта, указанного преподавателем, при значениях требуемой точности вычислений ε = 0.1; ε = 0.001; ε = 0.00001.
15
2) Оформить программы и протоколы решения задачи для каждого мето-
да.
3) Сравнить результаты выполнения задания для различных методов оптимизации и оценить скорость сходимости рассмотренных методов.
Таблица – Исходные данные для выполнения заданий
№ варианта |
|
|
Функция f(x) |
Отрезок [a, b] |
||||
1 |
|
x4 + 2x2 + 4x + 1 |
[ -1, 0 ] |
|||||
2 |
|
x5 - 5x3 + 10x2 - 5x |
[ -3, -2] |
|||||
3 |
|
x2 + 3x (ln(x) - 1) |
[ 0.5, 1] |
|||||
4 |
|
|
x2 - 2x -2 cos(x) |
[ 0.5, 1] |
||||
5 |
1 |
|
|
[ 0.5, 2] |
||||
|
|
|
|
|
|
|
||
|
(sin(x)+ cos(x))2 + x 2 |
|||||||
|
|
|
||||||
6 |
- x3 +3 (1 + x) (ln(1 + x) - 1) |
[-0.8, 0.5] |
||||||
7 |
|
|
|
cos(x) |
[ 7.5, 11] |
|||
|
|
|
|
x 2 |
|
|||
|
|
|
|
|
|
|||
8 |
|
|
(x - 4)2 + ln(x) |
[ 0.5, 8 ] |
||||
|
|
|
|
|
+ exp(- 2x) |
|
||
9 |
|
|
1 + x 2 |
[ 0, 1.5 ] |
||||
10 |
exp(x) + exp(- 2x) + 2x |
[ -1.5, 1.5 ] |
||||||
11 |
|
- sin(x) exp( -0.5x) |
[ -0.5, 2.5 ] |
|||||
12 |
|
|
tg(x) - 2sin(x) |
[ 0, 0.75 ] |
||||
БИБЛИОГРАФИЧЕСКИЙ СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Основы алгоритмизации вычислительных процессов: метод. указания по курсу «Информатика» для студентов 1-го курса всех спец. / Воронеж. гос. арх. - строит. ун-т; сост.: В.П. Авдеев, Г.Т. Венгерова, В.И. Гильмутдинов, А.Д. Кононов, А.А. Кононов. – Воронеж, 2005. – 41 с.
2.Супрун, А.Н. Вычислительная математика для инженеров-экологов. Методическое пособие / А.Н. Супрун, В.В. Найденко. – М.: АСВ, 1996. – 392 с.
3.Лапчик, М.П. Численные методы / М.П. Лапчик, М.И. Рагулина, Е.К. Хеннер. – М.: Academia, 2004. – 384 с.
ОГЛАВЛЕНИЕ |
|
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
3 |
1. Прямые методы оптимизации . . . . . . . . . . . . . . . . . . . . |
3 |
1.1. Метод равномерного поиска . . . . . . . . . . . . . . . . . . |
3 |
1.2. Метод поразрядного приближения . . . . . . . . . . . . . . |
3 |
1.3. Метод деления отрезка пополам . . . . . . . . . . . . . . . . |
5 |
1.4. Метод золотого сечения. . . . . . . . . . . . . . . . . . . . . |
7 |
1.5. Метод Фибоначчи . . . . . . . . . . . . . . . . . . . . . . . . |
9 |
1.6. Метод квадратичной интерполяции – экстраполяции . . . . |
9 |
2. Методы минимизации, основанные на использовании |
|
производных функций . . . . . . . . . . . . . . . . . . . . . . . |
11 |
2.1. Метод касательных . . . . . . . . . . . . . . . . . . . . . . . |
11 |
2.2. Метод Ньютона . . . . . . . . . . . . . . . . . . . . . . . . . |
13 |
3. Задание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
14 |
Библиографический список рекомендуемой литературы . . . . . . |
15 |
Одномерная оптимизация функций
Методические указания по курсу «Информатика» для студентов II курса всех специальностей
Составители: к. т. н., доц. Гильмутдинов Владимир Исламович, к. ф.-м. н., доц. Кононов Александр Давыдович,
д. т. н., проф. каф. ММВТ Кононов Андрей Александрович
Подписано в печать 06.04.2009. Формат 60×84 1/16. Уч.- изд. л. 1,0. Усл. - печ. л. 0,9. Бумага писчая. Тираж 230 экз. Заказ №
________________________________________________________________
Отпечатано: отдел оперативной полиграфии Воронежского государственного архитектурно-строительного университета
394006 Воронеж, ул.20-летия Октября, 84
