
Методическое пособие 612
.pdf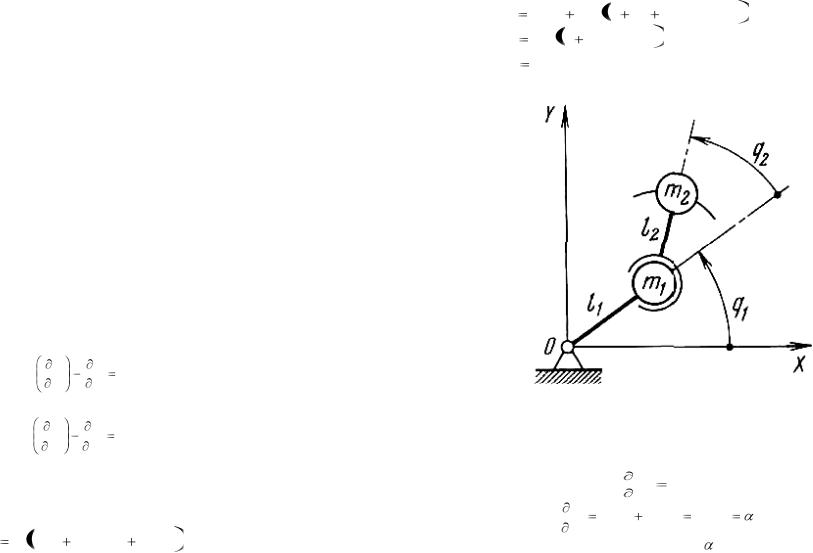
для роботов циклового типа, предназначенных для многократно повторяющихся движений. Заметим, что такой способ можно эффективно использовать и для управления механическими конечностями шагающих роботов, также совершающими циклические движения. В тех случаях, когда экономия энергозатрат оправдывает вычислительные затраты на планирование каждой отдельной операции (например, в космической робототехнике), этот метод может быть использован и для управления крупными манипуляторами, перемещающими большие инерционные нагрузки. Метод был разработан в середине 80-х годов в Институте машиноведения АН СССР [57;
58].
Рассмотрим метод планирования собственных движений на примере манипулятора, имеющего кинематическую схему, приведенную на рис. 4.5. Это двухзвенник, причем массы звеньев сосредоточены на концах жестких стержней. Такую конструкцию называют двойным плоским маятником.
Будем считать, что манипулятор снабжен устройствами статического уравновешивания. Поэтому в уравнении Лагранжа второго рода (§6.1) можно положить U=0; кроме того, Q =0, так как рассматривается собственное движение, и мы получим
|
d |
|
|
K |
|
|
K |
0, |
(4.86) |
|
|
|
|
|
|
|
|
|
|
||
|
dt |
|
|
q1 |
|
|
q1 |
|||
|
|
|
|
|
|
|
||||
d |
|
|
K |
|
|
K |
0. |
|
||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
q2 |
|
|
q2 |
|
|||
|
|
|
|
|
|
|||||
Кинетическая энергия К представляет собой квадратичную форму относительно скоростей обобщенных координат:
K |
1 |
2 |
|
2 |
(4.87) |
2 |
a11q1 |
2a12q1q2 |
a22q2 . |
||
|
|
|
|
|
Коэффициенты aij нетрудно определить (см. § 6.1 ). Они равны в данном случае:
a |
m l 2 |
m |
2 |
l 2 |
l 2 |
2l l |
cosq |
2 |
, |
||||
11 |
1 1 |
|
1 |
2 |
|
1 2 |
|
|
|||||
a |
m |
2 |
l 2 |
l l |
|
cosq |
2 |
, |
|
|
|
||
12 |
|
2 |
1 2 |
|
|
|
|
|
|
||||
a22 |
m22l22 . |
|
|
|
|
|
|
|
|
|
|
||
Нетрудно видеть, что эти коэффициенты не зависят от q1 ,. Поэтому и из первого уравнения системы (4.86) мы получим
|
|
|
K |
0 |
(4.88) |
|
K |
|
|
q1 |
|
||
|
|
|
|
|||
a11q1 |
a12 q2 |
const |
||||
|
||||||
q1 |
||||||
|
|
|
|
|
||
Физический смысл параметра — это кинетический
160
159

момент механизма относительно оси О подвеса манипулятора..
Второе уравнение (4.86) может быть использовано для получения уравнения движения. Для его анализа нужно также принять во внимание, что в свободном движении
K |
1 |
2 |
|
|
|
|
|
2 |
|
|
const |
h |
(4.89) |
|||
|
|
|
||||||||||||||
2 |
a11q1 |
2a12 q1q2 |
a22 q2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последнее уравнение в плоскости |
q1 , q2 |
определяет эл- |
||||||||||||||
липс, показанный на рис. 4.6 . При q1 0 получим |
|
|||||||||||||||
|
|
q2 |
|
2h |
|
|
|
|
|
2h |
|
|
, |
|
|
|
|
|
|
a22 |
|
|
|
m2 l22 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а при q2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
2h |
|
, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
a11 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Последняя величина зависит от q2, играющего роль па- |
||||||||||||||||
раметра. При его изменении меняются также размеры главных полуосей эллипса a, b и углы их наклона.
Производная |
K |
|
принимает максимальное значение в |
|||
|
|
|||||
q1 |
|
|||||
|
|
|
|
|
|
|
точке 4, а минимальное — в точке 3; эти значения равны |
||||||
|
|
|
|
|
|
|
max |
|
2ha11 , min |
2ha11. |
|||
4.7.3. Планирование движения манипулятора по собственной траектории
|
|
a12 |
|
2a11h |
2 |
|
|
||
q2 |
q2 |
|
|
, |
(4.91) |
||||
a |
|
a |
a |
22 |
a 2 |
||||
|
|
11 |
11 |
|
12 |
|
|
||
161
162
В точках 5 и 6, координаты которых нетрудно определить,  0 . При свободном движении изображающая точка на плоскости q1 , q2 должна принадлежать семейству эллипсов
0 . При свободном движении изображающая точка на плоскости q1 , q2 должна принадлежать семейству эллипсов
(меняющихся в зависимости от текущего значения q2). С другой стороны, в силу условия (4.88), эта точка должна совпадать в каждый момент времени с теми точками эллипсов, которые соответствуют одному и тому же значению кинетического момента. Последнее определяется при задании начальных условий q10 , q20 , q20 ; теперь условие (4.88) представляет собой еще
одно ограничение, связывающее q2 с текущими значениями q1 , q2 . Нетрудно получить параметрические уравнения траектории изображающей точки в форме [58]
|
|
|
|
a12 |
|
|
2a11h |
2 |
|
|
|||||
q1 q2 |
|
|
|
|
|
|
|
|
, |
(4.90) |
|||||
|
a |
a |
|
a |
a |
22 |
|
a 2 |
|||||||
|
|
|
|
|
|
|
|||||||||
|
11 |
11 |
|
11 |
|
12 |
|
|
|||||||
причем знак перед корнем соответствует знаку q2. |
|||||||||||||||
Теперь для приращения q1 |
q1 (T ) |
|
q1 (t0 ) |
может быть на- |
|||||||||||
писан следующий интеграл: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
q2 T |
q |
q |
2 |
|
|
|
|
|
||||
|
q |
|
|
|
1 |
|
|
|
dq |
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
1 |
|
|
|
q2 |
q2 |
|
|
|
|
|||||
|
|
|
q2 t0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разбивая пределы интегрирования на интервалы, в каждом из которых q2 сохраняет постоянный знак, можно определить этот интеграл, используя выражения (4.90) и (4.91). Левая часть выражения (4.92), т.е. q1 , задана условиями задачи. Известно также и q1 q1 (T ) q1 (t0 ) , относительно этой величины предположим, что q2 2 .
.
Из соотношения (4.92) можно с использованием численных методов найти . В соответствии с (4.90) и (4.91) по вычисленным значениям определяют начальные значения скоро-
163
стей q10 и q20 , траекторию движения в пространстве обобщенных координат, а также время движения. Последнюю величину можно вычислить по формуле
|
q2T |
dq2 |
|
|
t |
. |
|
|
q0 |
||
|
q20 |
|
|
|
|
|
|
На рис. 4.7 показаны траектории собственного движения |
|||
рассматриваемого |
манипулятора |
при значениях парамет- |
|
ров l1 1.1; l2 1; |
m1 m2 1 Для различных граничных усло- |
||
вий [58]. На рис. 4.7, а показано перемещение, в результате которого конфигурация механизма сохраняется, но с поворотом
относительно базовой оси, |
т.е. q20 |
q2T 1. На рис. 4.7, |
б рас- |
|||
смотрен случай, когда q20 |
1.57; |
q2T |
1; |
q10 |
0; q1T |
1. На |
|
|
|||||
рис. 4.7, в показано движение, которое приводит к зеркальному изменению положения манипулятора относительно оси, соединяющей точку подвеса маятника и центра тяжести второго звена.
Полученные траектории существенно отличаются от программных траекторий, найденных традиционными метода-
ми, |
например при выборе a) |
q1 const, |
q2 const |
или б) |
|
|
|
|
|
x1 |
const , x2 const , т.е. при прямолинейном движении схвата в |
|||
|
|
|
|
|
пространстве сцены. В [58] показано, что движение по собственной траектории на рис. 4.7; б экономичнее в 1,23 раза, чем движение по программной траектории в случае «а» и в 4 раза, чем в случае «б». Рассматриваемый метод в дальнейшем был усовершенствован и распространен на механизмы с тремя и более степенями подвижности [58]. Он позволил создать семейство промышленных роботов, обеспечивающих существенную экономию энергозатрат. Аналогичный подход был положен и в основу разработки исполнительных механизмов с динамическим уравновешиванием звеньев.
164
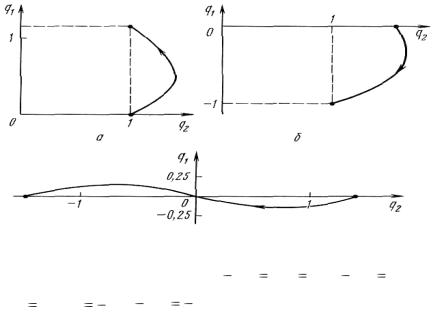
Рис. 4.3. Траектории собственного движения манипулятора на плоскости
обобщенных координат: |
a q20 q2T 1; б q20 1.57; |
|
q |
2T |
1; q |
1; в q20 |
q2T . |
|
1T |
|
|
165
Заключение
При выборе управляющих сигналов в главе 3 использовались только кинематические соотношения, далее, в главе 4, проводился анализ кинематического управления с учетом динамики манипулятора.
К методам динамического управления обычно относят такие, при которых формирование управляющих сигналов осуществляется с учетом уравнений динамики манипулятора. При этом за счет усложнения управления удается преодолеть негативное влияние нелинейностей и перекрестных связей, повысить качество процесса управления, обеспечить его устойчивость независимо от конкретной траектории. Такое управление приобретает особенно важное значение для манипуляторов, снабженных высоко моментными без редукторными электродвигателями, поскольку в этом случае неприемлемы методы расчета, основанные на разделении каналов управления.
Динамические методы представляют интерес при управлении крупными манипуляторами, перемещающими значительные инерционные нагрузки, например манипуляторами космических станций. Пренебрежение динамикой манипуляционных механизмов в этом случае принципиально не позволяет добиться необходимого качества и точности выполнения операций. Рассматриваемые в данной главе методы целесообразно использовать и при управлении промышленными манипуляторами, занятыми на операциях, связанных с преодолением внешних сил, в том числе на операциях сборки и механической обработки.
|
|
О Г Л А В Л Е Н И Е |
|
||
Введение. |
|
|
|
|
|
……………………………............................................... |
3 |
||||
1. ПРЕДСТАВЛЕНИЕ МЕХАНИЗМОВ И МАШИН |
|
||||
ДЛЯ АВТОМАТИЗИРОВАННОГО МОДЕЛИРОВА- |
|
||||
НИЯ………………………………….. |
17 |
||||
1.1. Представление объекта в виде механической цепи. |
17 |
||||
1.2. Классификация моделей компонентов и цепей… |
22 |
||||
1.3. Примеры механических цепей различных клас- |
|
||||
сов……………………………………………….. |
29 |
||||
2.ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ |
|
||||
СЛОЖНЫМИ (НЕОПРЕДЕЛЕННЫМИ) ДИНА- |
|
||||
МИЧЕСКИМИ СИСТЕМАМИ НА ОСНОВЕ |
|
||||
БИНАРНОГО ПОДХОДА……………… |
40 |
||||
2. 1. Требования |
к системам автоматического |
40 |
|||
управления в |
современной |
гпс…………………….. |
|||
|
|||||
2.2. Классический |
подход |
к структурному по- |
47 |
||
строению систем |
автоматического управления.. |
||||
|
|||||
2.3. Принцип бинарности……………………............... |
51 |
||||
|
|||||
2.4. Принципы |
регулирования и проблема |
57 |
|||
управления в |
условиях неопределенности………. |
||||
|
|||||
2.5. Обобщенные |
структурные схемы бинарных |
68 |
|||
систем автоматического управления……………… |
|||||
|
|||||
166
3. УРАВНЕНИЯ ЛАГРАНЖА………………………….. |
81 |
3.1. Уравнения лагранжа второго рода…………………... |
|
3.1.1. Структура уравнения………………………………. |
81 |
3..2. Движение при наличии внешних связей. Уравнения |
86 |
Лагранжа первого рода…………………………………… |
|
3.2.1. Определение реакции связей при использовании |
86 |
уравнений кинетостатики………………………………… |
|
3.2.3. Применение уравнений Лагранжа для анализа |
92 |
движения манипуляционных механизмов с замкнуты- |
|
ми контурами………………………………… |
|
3.3. Принцип Гаусса ………………………………………. |
103 |
3.3.1. Общая формулировка принципа Гаусса ……… |
|
3.3.2. Применение принципа Гаусса для исследования |
104 |
движения манипуляционных механизмов……………. |
|
3.3.3. Определение ускорений вынужденного движения… |
107 |
1. 4. МЕТОДЫ, ОСНОВАННЫЕ НА РЕ- |
113 |
ШЕНИИ ОБРАТНЫХ ЗАДАЧ ДИНА- |
|
МИКИ…………………. |
113 |
4.1. Компенсация динамики манипулятора в ре- |
|
альном времени……………………………………... |
|
4.2. Компенсация динамики программного движе- |
115 |
ния………………………………………………. |
|
4.3. Проблема реализуемости………………………… |
|
4.4. Обобщенный моментный регулятор……………. |
118 |
2. 4.5. Декомпозиция управле- |
120 |
ния……………………… |
123 |
4.5.1.Декомпозиция уравнений динамики манипуляционного механизма……………………….
4.5.2.Декомпозиция управляющих сигна-
лов………. |
125 |
4.6. Силовая обратная связь……………………… |
129 |
a. 4.6.1. Силовая |
132 |
обратная |
|
связь в соеди- |
138 |
167 |
|
нениях мани- |
143 |
пулято- |
|
ра…………… |
|
……………… |
150 |
……………. |
|
4.6.2. Силовая обратная связь на схвате…………….. |
151 |
4.6.3. Проблема устойчивости при силовой обратной |
154 |
связи……………………………………………………. |
|
4.7. Динамическое планирование…………………….. |
158 |
4.7.1. Планирование движения вдоль заданной траектории с учетом динамических ограничений…...
b. 4.7.2. Выбор мощности силовых агрега-
тов…………..
2. 4.7.3. Планирование движения манипулятора по собственной траекто-
рии…………………
…………….
Заключение……………………………………………..
Оглавление……………………………………………..
168
