
Методическое пособие 612
.pdf
ближенно, так как порядок числителя W 1 p может быть вы-
1 p может быть вы-
ше порядка знаменателя, т.е. нарушается условие физической реализуемости.
В соответствии с уравнением (4.11) управляющий сигнал g(t) можно получить, решив в реальном времени дифференциальное уравнение
M p g t N p μ t M p M q p q |
(4.12) |
|
в котором вектор управляющих сил и моментов μ t |
вычислен |
|
по формулам (4.2) |
или (4.6) (в обозначениях § 3.1). |
|
В частности, |
используя последнюю формулу для опре- |
|
деления μ t , получаем
Mp g t  N p *
N p *
*μ0 t A0 t  K1 q0 t
K1 q0 t  q t
q t  K2 q0 t
K2 q0 t  q t
q t  M
M p
p Mq p q t
Mq p q t 
или
M p g M p Mq |
p N p A0 K1 |
K2 p q |
||||
N p μ0 |
|
A0 K q0 |
K q0 |
(4.13) |
||
|
|
|||||
|
|
|
1 |
|
2 |
|
Если предположить, что программное движение реали- |
||||||
зуется точно |
и |
q |
q |
0 |
то соответствующий управляющий |
|
|
|
, |
||||
сигнал g°(t) будет удовлетворять дифференциальному уравнению
M |
p g0 t |
|
N p μ0 |
t |
|
M |
p |
M |
q |
p q0 t |
(4.14) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которое |
может |
быть |
решено |
предварительно. Полагая |
|||||||||||
g t |
~ |
g |
0 |
t , получаем для |
|
~ |
|
или, переходя к передаточ- |
|||||||
g t |
|
|
g t |
||||||||||||
ным функциям, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
~ |
|
|
0 |
|
|
0 |
q K2 q |
0 |
q |
M p M q p q q |
0 |
||
|
M p g t N p A |
|
t K1 |
q |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
119 |
|
|
|
|
|
|
W p g t |
A |
|
t K1 W p Wq p Δq t |
A |
|
t K2 |
q t |
(4.15) |
~ |
|
0 |
|
|
0 |
|
|
|
Таким образом, задачу вычисления корректирующей части g(t) управляющего воздействия можно свести к двум задачам, решаемым одновременно. Первая — это вычисление
правой части уравнения (4.15) |
t |
, для которой можно найти |
|||||||
интегральный оператор вида |
|
|
|
|
|
|
|
||
|
t |
|
|
|
|
0 |
|
|
(4.16) |
|
t |
t, |
q |
d |
A |
t K 2 |
|||
|
|
q t |
|||||||
|
t0 |
|
|
|
|
|
|
|
|
Вторая — решение интегрального уравнения Вольтерра |
|||||||||
первого рода, соответствующего (4.15) для g(t) : |
|
||||||||
|
t |
t |
~ |
d |
|
|
t |
|
(4.17) |
|
k |
g |
|
|
|
||||
|
t0 |
|
|
|
|
|
|
|
|
где |
k t |
L 1 W |
p |
|
|
|
|
|
|
Как известно, численное решение уравнения (4.17) связано с трудностями, обусловленными некорректностью этой задачи в смысле Тихонова*. Применяя методы регуляризации, можно приближенно решить и эту задачу.
4.4. Обобщенный моментный регулятор
Трудности реализации моментного управления с помощью обычной исполнительной системы (см. п. 4.1.3) связаны с тем, что при выборе моментного регулятора в виде (4.2) или (4.5) не были учтены возможности исполнительной системы. В результате, помимо решения обратной задачи динамики для механизма манипулятора, возникла еще одна обратная задача динамики для исполнительной системы. Проблему можно существенно упростить, рассматривая более общую, по сравне-
120

нию с (4.3), модель системы, которая должна быть получена в результате синтеза.
Взяв за основу задание вектора управляющих сил и моментов в виде (4.6), полагаем
μ μ0 A0W p q |
(4.18) |
где W p
p — диагональная передаточная матрица. В частно-
— диагональная передаточная матрица. В частно-
сти, при Wµ(p) = К1 + К2p получим прежнее соотношение (4.6). В общем случае компоненты W(p) являются дробнорациональными функциями оператора p:
W i |
p |
M |
i |
p |
|
|
|
|
|||
N |
i |
p |
|||
|
|
Подставляя формулу (4.18) в уравнение исполнительной системы (4.12), имеем
M  p g N p μ 0 N p A0W
p g N p μ 0 N p A0W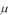 p
p q
q  M
M  p
p M q p
M q p q
q
Определяя программную часть управления g(t) попрежнему по формуле (4.14), получаем для корректирующей его части вместо (4.15) следующее соотношение:
~ |
0 |
W p W p Wq |
|
(4.19) |
M p g |
A |
p q |
Очевидно, что выбирая в выражении Wµ(p) порядок полинома Nµ (р) не ниже, чем порядок N(p) , а порядок Мµ(р) —
не выше, чем порядок М(р) , получаем физически реализуе-
~
мый оператор, связывающий управляющий сигнал g(t) клонением q(t) . Например, выбирая N (р) = N(p) , имеем
~ |
|
1 |
0 |
1 |
|
1 |
p Mq |
|
(4.20) |
g t |
M |
|
p N p A t N |
|
p M p E M |
|
p q t |
Подставляя вектор сил и моментов (4.18) в уравнение динамики механизма (4.1), получаем с учетом (4.5). Если предположить, что в малой окрестности опорного движения
q q0 121W p q0 q
q0 q
A q A q0 , BvT q
A q0 , BvT q BvT q0 и пренебречь слагаемым, содержащим B, то вместо (4.3) получим уравнение следующего вида:
BvT q0 и пренебречь слагаемым, содержащим B, то вместо (4.3) получим уравнение следующего вида:
или |
|
N p p 2 M p q 0 |
(4.21) |
Это уравнение обобщает (4.3). Оно определяет желаемые процессы в каждом из каналов управления. Параметры этих процессов и их устойчивость определяются корнями характеристических уравнений
N i |
2 |
M i |
0, i 1,2,...,N |
(4.22) |
|
В частности, полагая Nµ (р) = N(p) , получаем
N i |
2 |
M i |
0, i 1,2,...,N |
(4.23) |
|
Необходимое размещение корней на комплексной плоскости можно обеспечить путем выбора параметров полинома Мµi(λ). Итак, мы избавились от необходимости решать обратную задачу динамики для исполнительной системы ценой возможного ухудшения качества системы, получаемой в результате синтеза. Это связано с тем, что возможности коррекции положения корней характеристического уравнения (4.23) ограничены и существенно зависят от свойств исполнительной системы. Выбор того или иного способа коррекции, наиболее приемлемого для конкретного случая, — это вопрос опыта и умения разработчика.
4.5.Декомпозиция управления
4.5.1.Декомпозиция уравнений динамики манипуляционно-
го механизма
Под декомпозицией системы управления обычно подразумевают ее разделение на ряд более простых подсистем, каж-
122

дой из которых можно управлять по отдельности. Для систем управления манипуляторами декомпозицию можно осуществить путем компенсации перекрестных связей между каналами управления, порожденных динамикой манипуляционного механизма. Эти связи исследовались в гл. 7, причем гипотеза о том, что их влияние несущественно в рабочем диапазоне частот, была положена в основу рассмотренной в этой главе методики синтеза манипуляционной системы. В общем случае эта гипотеза не выполняется, в особенности для крупных манипуляционных конструкций большой грузоподъемности. Поэтому возникает проблема компенсации перекрестных связей путем специального формирования управляющих сигналов.
Наиболее просто эта задача решается в случае, когда в уравнении (4.1) можно пренебречь слагаемыми, нелинейно зависящими от скорости (центробежными и кориолисовыми силами), т.е. это уравнение можно представить в виде
|
T |
q G μ |
(4.24) |
A q q |
Bv |
Выберем вектор сил и моментов следующим образом:
μ BT |
q G |
A q A 1 |
q~ |
(4.25) |
v |
|
d |
|
|
где Ad(q) = diag[Au(q) A22(q) ... ANN(q)] — матрица, состоящая из диагональных членов матрицы A(q);
тогда вместо уравнения (4.24) получим систему из N уравнений второго порядка.
|
~ |
, i 1,2,...,N |
(4.26) |
Aii q q |
|
Воспользуемся уравнениями приводов (4.12), которые запишем в виде
Ni p i Mi Miq p qi |
(4.27) |
Таким образом, система разделена на N независимых подсистем и синтез ее сводится к синтезу каждой из подсистем
где i qi0 qi - сигналы ошибки.
Подставляя в эти уравнения значения ~i из (4.26), полу-
чим систему уравнений, определяющих движение N независимых подсистем:
N |
i |
p A q p 2 q |
i |
M |
i |
p |
i |
M |
iq |
p q |
i |
|
ii |
|
|
|
|
или
N |
i |
p A q p 2 |
M |
i |
p |
M |
iq |
p q |
i |
M |
i |
p g |
i |
(4.28) |
|
ii |
|
|
|
|
|
|
|
Каждый из каналов управления, описываемых нелинейным уравнением вида (4.28), теперь может быть синтезирован по отдельности в соответствии с предъявляемыми требованиями.
Поскольку в этой главе рассматривается управление вдоль программных движений q°(t) , выбранных заранее, матрицу Ad(q) также можно заранее рассчитать на программном
движении: |
A0 |
A q0 |
Полагая, что эта матрица незначитель- |
|
d |
d |
|||
|
|
но изменяется в малой окрестности опорного движения, можно записать уравнение в отклонениях от опорного движения, аналогичное (4.27), но линейное:
N |
i |
p A q0 |
t p 2 |
M |
i |
p |
M |
iq |
p q |
i |
M |
i |
p g |
i |
(4.29) |
|
ii |
|
|
|
|
|
|
|
|
Последнюю задачу решают путем выбора операторов Miε, Мiq(р) с помощью введения корректирующих устройств или путем изменения коэффициентов регуляторов, исходя из условий устойчивости и требуемого качества процесса управ-
123 |
124 |
|
123 |
||
|

ления в каждой из подсистем по отдельности (см. гл. 7). При этом обычно используют метод замороженных параметров, т.е. задачу решают для фиксированных значений Au(q0) в предположении, что элементы матрицы Ad(q0) изменяются существенно медленнее, чем процессы управления в приводах. Обычно удается выбрать постоянные параметры регулятора, обеспечивающие устойчивость и удовлетворительное качество системы «в среднем» вдоль всей траектории (см.
3.3).
4.5.2. Декомпозиция управляющих сигналов
Реализация подхода, рассмотренного в п.4.2.1 предполагает, как возможность прямого управления вектором управляющих сил и моментов в соответствии с уравнением (4.25), так и задание управляющего сигнала g(t) в соответствии с (4.28), обеспечивающего движение по программной траектории. Как уже отмечалось ранее, в § 4.1, такое управление недостижимо, если только не используется специальный привод, обеспечивающий прямое управление моментом. В обычных манипуляционных системах компенсация недиагональных составляющих в уравнении (4.24) должна выполняться путем специального формирования управляющих сигналов g, в которых можно выделить две части: сигнал динамической коррекции gd и сигнал локального управления g, , под которым подразумевают вектор сигналов управления отдельными каналами в предположении об их декомпозиции: g=gL+gd Сигнал gd должен обеспечить динамическую декомпозицию каналов. При этом система локального управления по-прежнему описывается уравнением (4.28), т.е.
N p A q p2 |
M p |
M |
q |
p q M p g |
L |
(4.30) |
d |
|
|
|
|
Динамическая коррекция может быть определена из уравнения динамики исполнительной системы в общем виде.
Подставляя в уравнение, связывающее вектор сил и моментов µ с вектором обобщенных координат q (4.11), выражение вектора µ из уравнения динамики механизма (4.24), получаем
|
T |
q G M p gL |
gd |
M p M q p q (4.31) |
N p A q q |
Bv |
С учетом выражения (4.30), определяющего локальное управление gL, запишем следующее уравнение для составляющей gd :
N p A q A q q |
BT q G M p g |
d |
d |
v |
или
1 |
q |
|
T |
q G M p g d |
(4.32) |
N p A q1 Ad |
E Ad q q |
Bv |
В последнем уравнении матрица A q Ad 1 q - Е характери-
зует перекрестные связи, обусловленные динамикой манипуляционного механизма. Уравнение (4.32) определяет сигнал динамической коррекции с учетом динамики исполнительной системы.
В частности, в окрестности программного движения,
обозначая как и выше |
|
A q0 |
|
A0 , A |
q0 |
A0 |
, BT q0 |
B0T , по- |
|
|
|
|
d |
|
d |
v |
vb |
лучаем |
|
|
|
|
|
|
|
|
N p A |
0 |
0 |
1 |
0 |
0T |
G |
M p g d |
(4.33) |
|
||||||||
|
Ad |
|
E Ad q |
Bv |
Поскольку процессы изменения во времени переменных матриц Ad0(t), Bv°T(t), A°(t), как правило, намного медленнее, чем процессы, обусловленные динамикой приводов, последней часто можно пренебречь при вычислении динамической
коррекции. В этом случае |
N p |
|
E , M |
p K = const |
и в со- |
|||||
ответствии с уравнением (4.33) найдем: |
|
|
|
|
||||||
0 |
K |
1 |
A |
0 |
0 |
1 |
0 |
0T |
G |
(4.34) |
|
||||||||||
g d g d |
|
|
Ad |
|
E Ad q |
Bv |
||||
Недостатком выбора динамической коррекции в форме (4.34)является чувствительность метода к ошибкам реализации. Поскольку матричные коэффициенты в правой части (4.34), реализуемые в системе управления, будут отличаться
125
126

от фактических, компенсация левой части уравнения (4.33) произойдет не полностью. В результате получим уравнение второго порядка (если пренебречь, как мы условились, динамикой привода) относительно q, решение которого q(t) может возрастать во времени.
|
Действительно, |
если обозначить для краткости |
|||||
ad |
A |
0 |
0 |
1 |
0 |
~ |
- приближенную реализацию этой мат- |
|
Ad |
|
E Ad |
, ad |
|||
рицы, |
|
|
|
|
|
|
|
|
|
ad |
ad |
~ |
- погрешность реализации ad ; аналогично |
||
|
|
ad |
|||||
g |
|
~ |
- |
погрешность реализации вектора статической на- |
|||
g g |
|||||||
грузки g |
Bv0T G то, подставляя фактически вычисленное в со- |
||||||
ответствии с (4.34) значение gd в (4.33), получаем при сделанных предположениях
ad q |
g |
|
|
|
или |
|
|
|
ad |
|
ad q |
0 g |
(4.35) |
|
|
|
|
|
q |
||||
|
|
|
|
|
|
|
|
|
|
где |
q |
q |
q |
0 |
При ненулевых начальных условиях решение |
||||
|
|
|
|
|
|
|
|
|
|
этого уравнения является возрастающей функцией времени, что приводит к накоплению ошибки. Значения коэффициентов матрицы ad , носят случайный характер как по величине, так
и по знаку, что позволяет надеяться на взаимную компенсацию ошибок во времени. Эту ошибку не удается ликвидировать за счет корректирующих связей самих приводов в уравнении (4.30), поскольку это уравнение характеризует процессы в отдельных каналах управления, а ошибки в соответствии с выбором gd в виде (4.34) накапливаются в перекрестных связях. Таким образом, влияние перекрестных связей может возрастать со временем функционирования системы.
Заметим, что погрешность будет накапливаться значительно быстрее, если вместо коррекции в форме (4.34) выбрать
127
программную динамическую коррекцию, заранее рассчитанную по формуле
g |
|
A0 A0 |
1 |
E A0q |
0 |
B 0T G |
d |
|
|||||
|
d |
|
d |
|
v |
1.В этом случае выражение (4.35) будет иметь вид:
a |
d |
q |
a |
d |
q0 |
g |
|
|
|
|
|
т.е. погрешность в этом случае накапливается даже при ad 0 . Другим источником погрешности является сделанное
допущение о том, что при выборе gd можно пренебречь динамикой приводов. Для того чтобы оценить его обоснованность, рассмотрим фактическое уравнение системы при коррекции вида (4.34). Предполагая при этом, что матричные коэффициенты в выражении gd реализованы точно в соответствии с уравнением (4.33), получаем
N p R 1M p A0 A0 |
1 |
E A0 q |
B 0T G E M p R 1 |
|
|||
d |
|
d |
v |
Это уравнение определяет закон изменения погрешности, обусловленной тем, что не учитывалась динамика привода. Устойчивость тривиального решения этого уравнения определяется корнями характеристического уравнения
det N |
K 1M |
A0 Ad0 |
1 |
E Ad0 2 0 |
(4.36) |
|
среди которых имеется нулевой корень, и, следовательно, система в лучшем случае находится на границе устойчивости. Это, как и в предыдущем случае, практически всегда приводит к накоплению ошибок в процессе работы системы.
Учесть динамику приводов, непосредственно определяя более точное значение gd из уравнения (4.33), невозможно, вследствие того, что передаточная матрица N(p)Mε(p) не удовлетворяет условию физической реализуемости. Однако можно попробовать найти приближенное решение задачи, учитывающее динамику приводов, используя тот же
128

прием, которым мы пользовались выше в § 4.1. В этом случае коррекция gd ищется как решение интегрального уравнения первого рода
t |
|
K gd0 t |
|
t |
t |
gd d |
|
0 |
|
|
|
где
 t
t L 1 N 1 p M p
L 1 N 1 p M p
a g0d t - значение динамической коррекции, определяемое по
формуле (4.34). Это уравнение может быть решено только приближенно. К тому же его необходимо решать в реальном масштабе времени в зависимости от значений g°d (t) , вычисляемых согласно (4.34). Из сказанного следует, что декомпозиция системы управления путем компенсации динамических связей связана с преодолением значительных трудностей, характер которых зависит от конкретной системы управления.
4.6.Силовая обратная связь
Одним из основных способов практической реализации методов динамического управления является силовая обратная связь. Ее реализуют с помощью датчиков сил и моментов, которые устанавливают либо в степенях подвижности манипулятора, либо в его «запястье», т.е. в сочленении захвата с основной конструкцией механической руки. В последнее время разрабатывают более сложные конструкции схватов, имеющих три и более «пальцев», которые также оснащают датчиками сил. Сигналы с датчиков обратных связей используются для формирования корректирующих сигналов с учетом моментов, действующих на манипулятор.
Использование датчиков моментов, расположенных в шарнирных степенях подвижности манипулятора, позволяет решить задачи динамической коррекции и декомпозиции (см.
4.1 и 4.2).
Спомощью датчиков сил и моментов, сосредоточенных
в«запястье» манипулятора, измеряют вектор сил и моментов, действующих со стороны нагрузки, например при выполнении механической работы. Такие датчики обычно используют для управления манипуляторами, предназначенными для операций сборки, механической обработки и т.д. Конструкция трехкомпонентного датчика сил показана на рис. 4.1. Датчик содержит ряд тензометрических элементов, которые при малой деформации конструкции под действием внешних сил позво-
ляют измерять трехкомпонентный вектор сил F = (F1 F2 F3) в декартовой системе координат, связанной с основанием датчика. Датчик может содержать встроенный микропроцессор, который выполняет обработку тензометрических сигналов и осуществляет обмен информацией с управляющей системой.
130
129

Рис. 4.1. Конструкция трехкомпонентного силомоментного датчика: I—1V— упругие элементы; 1-12 — чувствительные элементы (тензорезисторы)
Технические характеристики шестикомпонентного датчика, измеряющего векторы сил и моментов, можно найти в
[40].
Рассматриваемый датчик относится к числу пассивных устройств, т.е. предполагается, что коррекция движения по измеренным датчиком силам осуществляется за счет движений манипулятора в его степенях подвижности. Иногда, например при прецизионной сборке, точность, обеспечиваемая
манипулятором, оказывается недостаточной. Тогда применяют специальные активные модули, которые содержат как силомоментный датчик, так и систему приводов, обеспечивающих точное позиционирование, либо точную ориентацию схвата. Применение схвата с активными пальцами является развитием подхода, приближающего возможности схвата к возможностям кисти человеческой руки.
Таким образом, способы организации силовой обратной связи различны они зависят от конкретных задач, выполняемых роботом. Это предполагает и различные способы управления роботом с силовой обратной связью. Рассмотрим две основные группы таких способов.
4.6.1. Силовая обратная связь в соединениях манипулятора
В данном случае датчики сил или моментов, в зависимости от типа кинематической пары, устанавливают в соединениях манипулятора. Таким образом, с их помощью измеряют вектор сил и моментов ц, развиваемых в его степенях подвижности. Если предположить, что измерения идеальны, то их результатом является вектор цд, равный в соответствии с уравнениями (4.1)
Д |
A q q |
B q, q q |
Bv q G |
(4.37) |
|
|
|
T |
|
Поскольку этот вектор содержит полную информацию о динамических и статических силах и моментах, действующих на манипулятор в процессе его движения, его целесообразно использовать для формирования управляющего сигнала с целью компенсации динамических , эффектов и декомпозиции задачи управления.
Рассмотрим, например, управление (4.2), обеспечивающее полную декомпозицию задачи. Сопоставляя это выражение с формулой (4.37), можно заключить, что при наличии силовой обратной связи можно положить
131 |
132 |

μ |
μ Д |
K1 q |
K2 |
q |
q |
(4.38) |
|
где |
|
|
|
|
|
|
|
q q0 |
q; q |
q0 |
q; |
q |
q0 |
q |
|
Подставляя (4.38) в уравнение динамики механизма (4.1), |
|||||||
по-прежнему получаем (при |
det A q |
0 )уравнение (4.3), опи- |
|||||
сывающее систему, т.е. |
|
|
|
|
|
|
|
q K 2 q K1 q 0
При соответствующем выборе параметров матриц К1 и К2, будем иметь асимптотически устойчивое программное движение q0(t). Обратная связь по второй производной q здесь необязательна; можно выбрать
μ μ Д K1 q K2 q
что приведет к системе
K 2 q K1 q 0
которая также асимптотически устойчива при положительных параметрах матриц К1 и К2.
Нетрудно, используя силовую обратную связь, решить и задачу декомпозиции управления (см. § 4.2). В этом случае следует положить в качестве управляющего сигнала
~
|
~ |
(4.39) |
μ μ Д Ad q q |
μ |
где μ , как и в (4.25), означает вектор сил и моментов, разви-
ваемый приводами локальной системы управления, a Ad(q) — матрица, состоящая из диагональных членов матрицы A(q) (см. § 4.2). Согласно уравнению динамики (4.1) и соотношению (4.37), в этом случае систе р описывается уравнением
(4.26)
~
Ad q q μ
т.е. обеспечена декомпозиция многосвязной системы на локальные подсистемы. Выбирая, например,
~ |
Ad q q |
0 |
K1 |
q K 2 |
q |
μ |
|
(4.40) получаем уравнение системы, состоящей из отдельных подсистем:
Ad q q K 2 q K1 q 0
q K 2 q K1 q 0
Полагая в окрестности опорной траектории Ad(q) Ad(q0), нахо ро систему из 2N линейных уравнений второго порядка с переменными коэффициентами. Асимптотическая устойчивость решения обеспечивается выбором параметрических матриц Kt и К2 .
2.Заметим, что в выражениях (4.39), (4.40) можно
0 |
~ |
выбрать вместо Ad(q |
) постоянную матрицу Ad , совпадающую |
с Ad(q0) в одной из точек программной траектории, или даже произвольную диагональную матрицу постоянных коэффици-
ентов |
ˆ 0 |
. В последнем случае эти коэффициенты должны |
Ad |
обеспечивать асимптотическую устойчивость и необходимое качество переходных процессов в системе
ˆ
Ad q q K 2 q K1 q 0
Аналогично решается и задача декомпозиции для исполнительной системы. Выбирая, как и в § 4.2, управление приводами исполнительной системы в виде суммы локальной и динамической составляющих, положим, что локальная составляющая gL обеспечивает движение отдельно рассматриваемых приводов в соответствии с уравнением (4.30). С учетом (4.39), (4.11) уравнение для динамической коррекции gd примет вид
N p μ Д |
Ad q q M p gd |
(4.41) |
|
|
|
Если при определении gd можно пренебречь динамикой привода, и, кроме того, можно положить Ad(q)  Ad(q0) = Ad, то формула для динамической коррекции приобретет вид:
Ad(q0) = Ad, то формула для динамической коррекции приобретет вид:
g d K |
1 |
μ Д |
0 |
(4.42) |
|
Ad q |
где Kε — диагональная матрица коэффициентов. Сравнивая выражения (4.34) и (4.42), можно заметить, что в последнем
134133

случае вычисляются только диагональные члены матрицы A0 , а в первом — вся матрица.
Заметим, что при динамической коррекции в (4.41), (4.42) вместо Ad0, как и выше, может быть выбрана любая диа-
гональная матрица с постоянными коэффициентами: |
ˆ 0 |
0 |
Ad |
Ad |
Единственное требование, предъявляемое к ней, — обеспечение устойчивости и необходимого качества процессов в системе локального управления, которая описывается уравнением, аналогичным (4.30), но с постоянными коэффициентами:
ˆ 0 |
p |
2 |
M p M q p q M p g L |
(4.43) |
N p Ad |
|
Таким образом, используя силовую обратную связь, действительно можно решить те задачи, о которых шла речь в 4.1 и 4.2. Принципиальное отличие рассматриваемого способа управления состоит в том, что не требуется вычислять в реальном времени матричные коэффициенты в правой части выражений (4.2), (4.4), (4.34), так как сигнал цд снимается с датчиков. Поэтому отпадает одна из основных проблем динамической коррекции, связанная с неточностью динамической модели исполнительного механизма (4.1). Это касается как структуры динамической модели, так и значений ее параметров, которые на практике всегда известны лишь приблизительно.
Еще одна задача, для которой может эффективно использоваться силовая обратная связь, — это задача отработки наряду с заданной программой движения и заданного закона изменения сил (моментов), приложенных со стороны схвата к инструменту, или к объекту манипулирования. Характерным примером является задача механической обработки поверхности с помощью инструмента, закрепленного на конце манипулятора, например операции шлифовки или обдирки сложной поверхности.
Если F0(t) — закон изменения вектора сил вдоль заданной траектории, то закон изменения соответствующих моментов в степенях подвижности манипулятора характеризуется формулой:
ˆ 0 |
μ |
0 |
0 |
(4.44) |
μ |
|
μ F |
где μ 0 — программное изменение моментов вдоль траектории, вычисляемое по (4.5), a μ 0F — составляющая, обусловленная вектором сил F0:
μ0F J T q0 F0
(4..45)
Используем динамическую коррекцию для декомпозиции системы, выбрав на этот раз
gd M |
1 |
ˆ 0 |
μˆ |
0 |
(4.46) |
|
p N p μ Д Ad q |
|
Тогда для локальной составляющей g, вместо уравнения (4.43) получим
ˆ 0 |
M p |
ˆ |
0 |
(4.47) |
N p Ad q |
M q p q M p g L N p μ |
|
Это уравнение соответствует полученной в результате декомпозиции системе из N независимых каналов управления, входным сигналом для которых является вектор локального управления gL, , а нагрузкой — программное изменение μˆ 0 .
Поскольку вектор μˆ 0 определен заранее, можно
обычным путем исследовать ошибку, обусловленную нагрузкой и, при необходимости, ввести дополнительную коррекцию в приводы каналов управления.
В соответствии с (4.47) передаточную матрицу по возмущению определяют следующим образом:
ˆ 0 |
|
2 |
1 |
(4.48) |
|
p |
M p M q p N p |
||||
W p N p Ad |
|
Отклонение qµ(t) вектора q(t), вызванное нагрузкой μˆ 0 , можно определить так:
135
|
t |
0 d |
q t |
K t μˆ |
|
|
t0 |
|
где
k t
t  L 1 W
L 1 W p
p
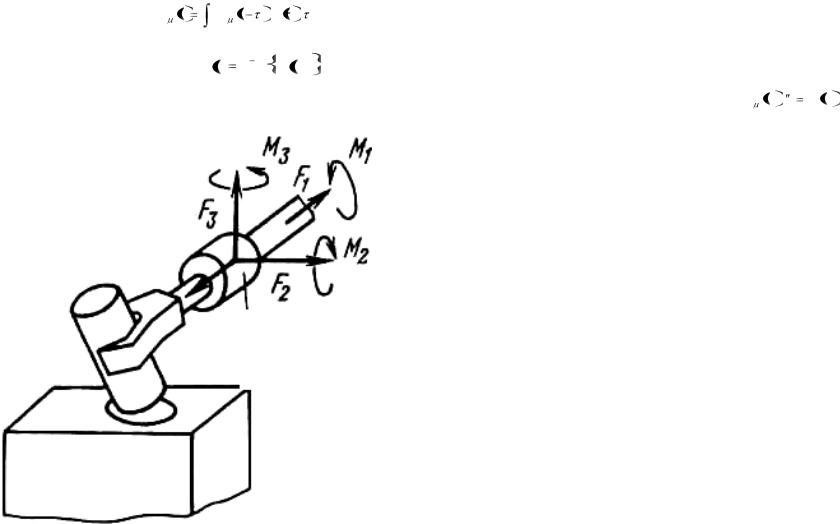
Рис. 4.2. Многомоментный датчик сил и моментов в запястье манипулятора
Методы введения коррекции, обеспечивающие уменьшение моментной ошибки, хорошо известны, и мы не будем здесь на них останавливаться. Отметим, что в данном случае
возмущение поддается предварительному расчету. Следовательно, можно выполнить коррекцию и за счет программного изменения управляющего сигнала. Положим в выражении (4.49) gL = g'L + g», где g'L определяется рограмммой движения, a gL» заранее вычисляют из соотношения
ˆ |
0 |
(4.50) |
M p g L N p μ |
|
Тогда для g'L уравнение приводов по-прежнему определяется формулой (4.43), а введение gL» позволяет полностью компенсировать программную нагрузку. Практически речь может идти только о приближенной реализации, как в случае вычислений по формуле (4.50), так и за счет других допущений, уже обсуждавшихся выше.
4.6.2. Силовая обратная связь на схвате
Под этим названием мы понимаем организацию силовой обратной связи в «запястье» манипулятора с помощью многокомпонентного силомоментного датчика, позволяющего измерить в общем случае шестикомпонентный вектор сил Ft и моментов М;, приложенных к схвату или инструменту, закрепленному на манипуляторе, со стороны объекта работ (рис. 4.2).
Такой способ наиболее эффективен для выполнения механических операций с помощью манипулятора. Если предположить известным закон изменения сил, ко-Матчик сил которых должен быть приложен со стороны и моментов манипулятора к нагрузке F0(t), то измеряя фактическое значение F0(t), можно вычислить управляющие моменты в степенях подвижности манипулятора, организуя обратную силовую связь. Выясним сначала, что же измеряет датчик сил и моментов на схвате.. Представим себе, что схват вместе с нагрузкой отделен от остальной конструкции манипулятора плоскостью, в которой производят измерение сил датчиком. Оставшаяся часть механизма движется в соответствии с уравнением вида
137136 |
138 |
