Основы квантовой статистики и физики твердого тела. учебное пособие. Москаленко А.Г., Гаршина М.Н

область CD – росту концентрации

собственных носителей. Таким образом, при низких температурах основной вклад в концентрацию носителей тока вносит примесная концентрация, при высоких температурах – концентрация собственных носителей.

3.5. Подвижность носителей в полупроводниках и ее зависимость от температуры

Электронный и дырочный газ в собственных и слабо легированных примесных полупроводниках является невырожденным, поэтому в отличие от металлов подвижность носителей, представляющая среднюю скорость их дрейфа в электрическом поле единичной напряженности (1.39), определяется усредненными значениями длины свободного пробега и скорости:

где ν – число столкновений в единицу времени.

В области высоких температур основное значение имеет рассеяние электронов и дырок на тепловых колебаниях решетки, т.е. фононах. При рассеянии носителей на фононах длина их свободного пробега обратно пропорциональна концентрации

<λ>~1/nф~1/T. Полагая здесь 1 , так как из-за высокого значения импульса фонона носители уже в единичных актах столкновения практически полностью теряют свою скорость, выражение для подвижности носителей в полупроводниках примет следующую зависимость:

В области низких температур подвижность носителей определяется их рассеянием на ионизированных примесных атомах. Рассеяние состоит в том, что ионы примеси отклоняют электроны, проходящие вблизи них, и тем самым уменьшают скорость их движения в первоначальном направлении. Чем выше скорость электронов и больше их эффективная масса, тем слабее отклоняются электроны от направления первоначального движения и тем больше число столкновений ν требуется для того, чтобы рассеять движение в этом

направлении. Согласно расчетам ~ 4 .

Учитывая также, что длина свободного пробега при рассеянии на ионизированных примесях обратно пропорциональна концентрации примесных атомов и от температуры не зависит, получим:

График зависимости u(Т) для полупроводников показан на рис. 3.7.

Таким образом, в области низких температур подвижность носителей заряда в полупроводниках обусловлена их рассеянием на ионизированных примесях и пропорциональна T3/2. В области высоких температур основное значение имеет рассеяние на фононах (тепловых колебаниях решетки) и подвижность носителей пропорциональна Τ -3/2.

72

3.6. Температурная зависимость электропроводности полупроводников

Удельная электропроводность собственного полупроводника обусловлена электронной и дырочной проводимостью и определяется выражением

электропроводности собственных полупроводников, исходя из зависимости от температуры концентрации носителей и их подвижности. В отличие от металлов, в которых электронный газ является вырожденным, концентрация носителей практически не зависит от температуры и температурная зависимость их проводимости целиком определяется температурной зависимостью подвижности носителей, в полупроводниках, наоборот, газ носителей является невырожденным и его концентрация весьма резко зависит от температуры (3.12). В этом случае степенной зависимостью подвижности от температуры (3.17) по сравнению с

73

экспоненциальной зависимостью концентрации можно пренебречь, представив выражение (3.18) в виде:

оси ординат, позволяет определить величину σ0, а тангенс угла ее наклона к оси абсцисс, равный Eg/2k, дает возможность определить ширину запрещенной зоны полупроводника.

Удельная электропроводность примесных полупроводников, обусловленная как собственными, так и примесными носителями (например, электронами), рассчитывается по формуле

зависимостью от температуры концентрации и подвижности собственных и примесных носителей. Схематически кривая зависимости lnσ от 1/Т представлена на рис.3.8,б.

Низкотемпературная область AB отвечает примесной проводимости полупроводника, возникающей вследствие ионизации примесных атомов и появления примесных носителей: электронов в полупроводниках с донорной примесью и дырок в полупроводниках с акцепторной примесью. Подвижность носителей при этих температурах определяется рассеянием на ионизированных атомах примеси (3.17). В первом приближении этой зависимостью по сравнению с экспоненциальной можно пренебречь, считая что:

74

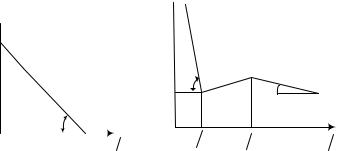
ln D

ln

ln 0

описывающее прямую АВ. Откуда, тангенс угла наклона прямой АВ к оси абсцисс равен

примесей Ts, которая тем выше, чем больше энергия активации примеси и ее концентрация, до температуры перехода к

заметного возбуждения собственных носителей, вследствие чего

зависимостью подвижности носителей. Если основным механизмом рассеяния носителей в рассматриваемой области является рассеяние на тепловых колебаниях решетки, для которого характерно уменьшение подвижности с ростом

температуры ( u ~ T 3/ 2 ), то проводимость на этом участке будет падать. Этот случай и показан на рис.3.8,б. Если же основным механизмом окажется рассеяние на ионизированных примесях, то подвижность, а, следовательно, и проводимость в области BC будет увеличиваться с ростом температуры.

Область CD соответствует переходу к собственной проводимости полупроводников. В этой области концентрация носителей резко возрастает за счет интенсивного возбуждения собственных носителей. Поэтому проводимость полупроводника в этой области определяется соотношением

(3.19):

Вполулогарифмических координатах n( ) =f(1/T)

графиком этой зависимости является прямая CD, образующая с осью абсцисс угол α2, тангенс которого пропорционален ширине запрещенной зоны Eg:

Зависимость сопротивления полупроводников от температуры используется для устройства термосопротивлений или термисторов.

3.7. Фотопроводимость полупроводников

Проводимость, приобретенная полупроводником под действием света, называется фотопроводимостью. Она обусловлена внутренним фотоэффектом. В полупроводнике под влиянием света образуются дополнительные носители тока: электроны и дырки. Увеличение концентрации свободных

76

носителей заряда влечет за собой увеличение проводимости

где σ0 – основная (тепловая) электропроводимость, обусловленная тепловым возбуждением носителей заряда, σф – электропроводимость, вызванная появлением избыточных носителей.

Избыточные носители являются неравновесными: после прекращения освещения они рекомбинируют и восстанавливается прежняя величина проводимости, характерная для необлученного полупроводника при данной температуре, называемая “темновой проводимостью”.

Различают собственную и примесную фотопроводимость. Схема образования собственной фотопроводимости показана на рис.3.9,а. Фотон с энергией hv>Eg поглощается и переводит электрон из валентной зоны в зону проводимости. Образующаяся при этом пара электрон-дырка является свободной и участвует в создании проводимости полупроводника. Красная граница этой проводимости, т.е. максимальная длина волны, при которой свет является еще фотоэлектрически активным, определяется выражением

фотопроводимости приходится на видимую часть спектра.

На рис. 3.9 показана схема образования под действием света дополнительных примесных носителей в полупроводниках n-типа (б) и p-типа (в). В этих случаях фотон с энергией hv>Enp переводит электрон либо с донорного уровня в

где Епр есть энергия активации примесных (донорных или акцепторных) уровней. Примесный фотоэффект возможен лишь в том случае, если полупроводник находится при температуре ниже температуры истощения примеси. Поэтому для наблюдения примесной фотопроводимости полупроводник необходимо, как правило, охлаждать. Красная граница

Энергетический спектр экситонов является дискретным

(рис. 3.10).

Уровни энергии экситонов располагаются у дна зоны проводимости. Так как экситоны являются электрически

78

нейтральными системами, то возникновение их в полупроводнике не приводит к появлению дополнительных носителей заряда, вследствие чего поглощение фотона не сопровождается увеличением проводимости полупроводника. Возникнув, экситоны некоторое

время блуждают по объему полупроводника. При столкновении с фононами, примесными центрами и другими несовершенствами решетки экситоны или рекомбинируют, или разрываются. В первом случае энергия возбуждения передается узлам решетки или излучается в виде квантов света (люминесценция), во втором случае образуется пара носителей – электрон и дырка. Они обусловливают фотопроводимость полупроводника.

Приборы, действие которых основано на явлении фотопроводимости, называют фотосопротивлениями (ФС) или фоторезисторами. Устройство фотосопротивления показано на рис.3.11. Здесь 1 – полупроводниковый слой, 2 – подложка, 3 – металлические электроды, 4 – защитное лаковое покрытие. Для получения фототока необходимо в цепь последовательно с ФС включить источник постоянного тока.

U const

Ф 0

IT

Ф2 Ф1

Рис. 3.12. Рис. 3.13.

79