
Методические указания к практическим занятиям по дисциплине «Криптографические методы защиты информации». Мокроусов А.Н
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра систем информационной безопасности
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по дисциплине «Криптографические методы защиты информации» для студентов специальностей
090301 «Компьютерная безопасность»,
090302 «Информационная безопасность телекоммуникационных систем», 090303 «Информационная безопасность автоматизированных систем»
очной формы обучения
Воронеж 2014
Составитель канд. техн. наук А. Н. Мокроусов
УДК 681.326
Методические указания к практическим занятиям по дисциплине «Криптографические методы защиты информации» для специальностей 090301 «Компьютерная безопасность», 090302 «Информационная безопасность телекоммуникационных систем», 090303 «Информационная безопасность автоматизированных систем» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. А. Н. Мокроусов. Воронеж, 2014. 47 с.
Методические указания предназначены для студентов четвертого и пятого курсов, выполняющих практические занятия по изучению криптографических методов защиты информации. Рассмотрены также элементы теории чисел в разделах «Модулярная арифметика» и «Алгебраические структуры».
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2013 и содержатся в файле Мокроусов_ПЗ_КМЗИ.pdf.
Ил. 3. Табл. 8. Библиогр.: 13 назв.
Рецензент д-р техн. наук, проф. А. Г. Остапенко
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А. Г. Остапенко
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский государственный технический университет», 2014
Практическое занятие № 1 Алгоритм Евклида для нахождения общего делителя
Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел [1].
Вспомним математику. Наибольший общий делитель двух натуральных чисел – это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НОД(12, 18) = 6.
Обозначим исходные данные как М u N. Постановка задачи выглядит следующим образом:
Дано: М, N
Найти: НОД(М, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД (М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Идея алгоритма Евклида
Идея этого алгоритма основана на том свойстве, что если M>N, то
НОД(М, N) = НОД(М - N, N).
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К - общий делитель М u N (M> N). Это значит, что М = mК, N = nК, где m, n - натуральные числа, причем m > n. Тогда М - N = К(m - n), откуда следует, что К - делитель числа М - N. Значит, все общие делители чисел М и N являются делителями их разности М - N, в том числе и наибольший общий делитель.
Второе очевидное свойство:
НОД(М, М) = М.
Для «ручного» счета алгоритм Евклида выглядит так:
1)если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2)заменить большее число разностью большего и меньшего из чисел;
3)вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
М |
32 |
8 |
8 |
8 |
N |
24 |
24 |
16 |
8 |
Получили: НОД(32, 24) =НОД(8, 8) = 8, что верно.
На рис. 1 приведена блок-схема алгоритма Евклида. Структура алгоритма – цикл с вложенным ветвлением.
Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
2
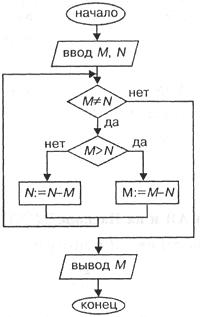
Рис. 1. Блок-схема алгоритма Евклида
Ниже представлена табл. 1 алгоритма для исходных значений М = 32, N = 24.
|
|
|
|
Таблица 1 |
|
|
Алгоритм Евклида |
|
|
||
Шаг |
Операция |
M |
N |
Условие |
|
1 |
ввод М |
32 |
|
|
|
2 |
ввод N |
|
24 |
|
|
3 |
M ¹ N |
|
|
32 ¹ 24, да |
|
4 |
M>N |
|
|
32>24, да |
|
5 |
M:=M-N |
8 |
|
|
|
6 |
M ¹ N |
|
|
8 ¹ 24, да |
|
7 |
M>N |
|
|
8>24, нет |
|
8 |
N:=N-M |
|
16 |
|
|
9 |
M ¹ N |
|
|
8 ¹ 16, да |
|
10 |
M>N |
|
|
8>16, нет |
|
|
|
3 |
|
|
|
|
|
|
Продолжение табл. 1 |
||
11 |
N:=N-M |
|
8 |
|
|
12 |
M ¹ N |
|
|
8 ¹ 8, нет |
|
13 |
вывод M |
8 |
|
|
|
14 |
конец |
|
|
|
|
В итоге получился верный результат.
Контрольные вопросы:
1.Что такое наибольший общий делитель двух натуральных чисел?
2.На каком свойстве основана идея алгоритма
Евклида?
3.Какова блок-схема алгоритма Евклида?
4.Приведите различные примеры шифротекстов.
5.Приведите примеры криптограмм для заданных открытых данных.
4
Практическое занятие № 2 Расширенный алгоритм Евклида
При заданных неотрицательных целых |
[2,3,9,10] |
числах а и b этот алгоритм определяет вектор
(u1, u2, u3),
такой, что
а* u1+ b * u2 = u3 = НОД (a, b).
Впроцессе вычисления используются вспомогательные векторы (v1, v2, v3), (t1, t2, t3). Действия с векторами производятся таким образом, что в течение всего процесса вычисления выполняются соотношения
а * t1 a * u1 a * v1
+b * t2 = t3,
+b * u2= u3,
+b * v2 = v3.
Для вычисления обратной величины a-1 (mod n) используется частный режим работы расширенного алгоритма Евклида, при котором Ь = n , НОД (а, n)=1, и этот алгоритм определяет вектор
(u1, u2, u3),
такой, что
u3 = 1, a * u1 + n * u2 = НОД (а, n) = 1,
(а * u1+ n * u2) mod n  а * u1(mod n)
а * u1(mod n)  1. a-1 (mod n)
1. a-1 (mod n)  u1 (mod n).
u1 (mod n).
Шаги алгоритма :
1.Начальная установка .
Установить (u1, u2, u3) := (0, 1, n), (v1, v2, v3) := (1, 0, a).
2.u3 = 1?. Если u3 = 1, то алгоритм заканчивается.
3.Разделить, вычесть.
Установить q :=[ u3 / v3 ].
5
Затем установить
(t1, t2, t3) := (u1, u2, u3) - (v1, v2, v3) * q, (u1, u2, u3) := (v1, v2, v3),
(v1, v2, v3) := (t1, t2, t3).
Возвратиться к шагу 2.
Пример 1. Заданы модуль n = 23 и число а = 5. Найти обратное число a-1 (mod 23), т. е. x=5-1 ( mod 23).
Используя расширенный алгоритм Евклида, выполним вычисления, записывая результаты отдельных шагов в табл.2.
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
|
Расширенный алгоритм Евклида |
|
|
|
||||
q |
u1 |
|
u2 |
u3 |
v1 |
|
v2 |
|
v3 |
- |
0 |
|
1 |
n = 23 |
1 |
|
0 |
|
а = 5 |
4 |
1 |
|
0 |
5 |
-4 |
|
1 |
|
3 |
1 |
-4 |
|
1 |
3 |
5 |
|
-1 |
|
2 |
1 |
5 |
|
-1 |
2 |
-9 |
|
2 |
|
1 |
- |
-9 |
|
2 |
1 |
|
|
|
|
|
При u3= 1, u1= -9, u2= 2
(а * u1 + n * u2 ) mod n = (5 * (-9) + 23 * 2) mod 23 = = 5*(-9) mod 23  1,
1,
a-1 (mod n) = 5-1 (mod 23) = (-9) mod 23 = (-9 + 23) mod 23 = 14.
Итак , х = 5-1(mod 23)  14 (mod 23) = 14.
14 (mod 23) = 14.
Для решения более сложных сравнений
а * х  b (mod n), т. е. b≠1, х = ?
b (mod n), т. е. b≠1, х = ?
используется следующий прием. Сначала решают сравнение
а* у  1(mod n), т. е. определяют
1(mod n), т. е. определяют
у= a-1( mod n), а затем находят
х= a-1 b (mod n) = у * b (mod n).
6
Пример 2. Найти х для сравнения
5 * х  9 (mod 23).
9 (mod 23).
Сначала решаем сравнение
5 * y  1(mod 23).
1(mod 23).
Получаем у = 5-1(mod 23) = 14. Затем находим
х= 5-1 * 9 (mod 23) = 14 * 9 (mod 23) =
=126 (mod 23)  11 (mod 23),
11 (mod 23),
x= 11.
Контрольные вопросы:
1.Какой вектор определяет расширенный алгоритм
Евклида?
2.Каковы шаги расширенного алгоритм Евклида?
3.Привести примеры шифрования и расшифрования
данных.
4.Что такое целостность информации?
5.Что означает восстановить открытый текст?
7
Практическое занятие № 3 Вычисление обратных величин
В арифметике действительных чисел [7, 8] нетрудно вычислить мультипликативную обратную величину а-1 для ненулевого а:
а-1 =1/а или а * а-1 = 1.
Например, мультипликативная обратная величина от числа 4 равна 1/4, поскольку
4 * 1/4 = 1.
В модулярной арифметике вычисление обратной величины является более сложной задачей. Например, решение сравнения
4 * x  1( mod 7)
1( mod 7)
эквивалентно нахождению таких значений х и к, что
4 * х  7 * к +1,
7 * к +1,
где х и к - целые числа.
Общая формулировка этой задачи - нахождение такого целого числа х , что
a * x (mod n)=1.
Можно также записать
а-1  x (mod n).
x (mod n).
8
