
Методическое пособие 296
.pdf
Пример 2. Найти
Так как |
x |
2 |
2x 4 |
x |
||||
|
||||||||
|
|
|
x |
2 |
2x 4 |
|
||
|
|
|
|
|
|
|
||
Тогда |
|
|
x 1 |
|
dx |
|||
|
|
|
|
|||||
|
|
|
|
|
|
3 |
|
|
|
|
|
x |
2 |
2x 4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x 1 |
|
dx . |
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
2 |
5 |
, то |
x 1 t , |
x |
|||||||
|
|
|||||||||||
|
|
|
|
|
t |
2 |
|
5 |
|
|
|
|
|
|
|
|
|
t |
3 |
dt . Положим |
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t 1 |
, dx |
t |
5 |
|
|
sin z |
|
dt .
, тогда
dt |
|
5 cos z |
dz |
, |
z arcsin |
|
|
5 |
. Следовательно, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
sin |
2 |
z |
|
|
t |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
t |
2 |
5 |
|
|
|
|
|
5 |
|
5 |
|
|
5 cos z |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
dt |
|
sin |
z |
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
cos |
2 |
z dz |
|
|
|
||||||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
sin |
|
z |
|
|
5 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
1 cos 2z |
dz |
|
|
5 |
z |
1 |
sin 2z |
|
dz C |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
5 |
|
|
|
|
2 |
|
|
|
|
|
10 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
5 |
|
|
|
|
|
5 |
|
1 |
sin |
|
2 arcsin |
|
|
5 |
|
|
|
|
|
|
|
5 |
arcsin |
|
5 |
|
|
||||||||||||
|
|
|
arcsin |
|
|
|
|
|
|
|
|
C |
|
10 |
|
|
|
|||||||||||||||||||||||||
|
|
10 |
|
|
|
|
|
t |
|
2 |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 4 |
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
x |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
sin |
|
2 arcsin |
|
|
|
|
C |
|
|
|
arcsin |
|
|
|
|
|
|
x 1 |
2 |
|
C. |
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
10 |
|
|
|
x 1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
8.3. Интегрирование дифференциальных биномов
Интегралы типа
|
|
|
|
|
|
|
|
|
x |
m |
|
a bx |
n |
p |
dx |
|
|
|
|
|
(интегралы от диффе-
ренциального бинома), где a, b – действительные числа; m, n – рациональные числа, выражаются через элементарные функции
только в том случае, если хотя бы одно из чисел p, |
m 1 |
или |
|||
n |
|
||||
|
|
|
|||
m 1 |
p является целым. |
|
|
|
|
n |
|
|
|
||
|
|
|
|
||
Приведение интеграла к интегралу от рациональной функции осуществляется следующими подстановками:
29

1. Если p – целое число, то подстановка |
x |
наименьшее общее кратное знаменателей дробей m и
2. Если |
m 1 |
- целое число, то подстановка |
|
n |
|||
|
|
t |
k |
, |
|
||
n. |
|
|
a |
||
где k
bx |
n |
t |
|
–
s |
, |
|
где s – знаменатель дроби p.
3. Если |
m 1 |
p |
– целое число, то подстановка |
|||||
n |
||||||||
|
|
|
|
|
|
|
||
a bx |
n |
n |
t |
s |
, где s – знаменатель дроби p. |
|||
|
x |
|
||||||
Во всех остальных случаях интегралы от дифференциального бинома не выражаются через элементарные функции, т.е. не берутся.
|
Пример. |
Найти |
|
|||||||||
m |
1 |
, |
n |
1 |
, |
p |
1 |
, |
||||
2 |
4 |
3 |
||||||||||
|
|
|
|
|
|
|
|
|||||
4 |
x 1 |
t |
3 |
, тогда |
x t |
|||||||
|
|
|||||||||||
Следовательно,
3
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
4 |
|
|
|
|
1 |
|
|
1 |
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
dx |
|
|
x |
|
2 |
1 x |
4 |
|
dx . |
|
Здесь |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 1 |
2 . Поэтому делаем подстановку |
|||||||||||||||||||
n |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
4 |
, |
dx 4 t |
3 |
1 |
3 |
3t |
2 |
dt |
, |
t |
3 |
4 |
x 1 . |
||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
3 |
4 |
|
x 1 |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
t |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
dx |
|
|
|
|
|
12t2 |
|
t3 1 |
|
|
dt 12 |
|
|
t6 |
t3 |
|
dt 12 |
|
|
|
||||
|
|
|
|
x |
|
|
|
|
t |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
t |
4 |
|
12 |
|
|
|
|
|
7 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 |
|
|
3 |
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||
12 |
C |
|
x |
1 |
3 |
|
x 1 |
C. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
4 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи для самостоятельного решения
1. |
|
|
4.
x 7 |
dx |
|
x 9 |
||
|
3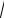 x2 25 dx
x2 25 dx
3 x 5
x 5
2. |
|
5.
1 |
|
x |
dx |
|
|
4 |
|
|
|
||
x |
|
|
|
||
|
|
|
|
||
|
6 |
x 1 |
dx |
||
6 x7 |
6 x5 |
||||
|
|||||
3. |
|
|
6.
|
|
1 |
dx |
|
x |
3 |
x 4 |
||
|
||||
|
|
|

 3x 1 dx
3x 1 dx
 3x 1 5
3x 1 5
30

|
|
x |
2 |
|
|
|
1 x |
|
|
||
7. |
|
|
3 |
1 |
x |
|
dx |
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
10. |
|
|
|
|
|
|
dx |
|
|
||
|
x |
3 |
3 |
x 3 |
2 |
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
13. |
|
|
|
|
|
|
1 |
|
dx |
|
|
|
x |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2x 5 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
16. |
|
|
|
|
|
|
dx |
|
|
|
|
|
4x |
2 |
2x 3 |
|
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
19. |
|
|
|
5x 7 |
dx |
|
|||||
|
|
|
|
|
|
|
|
||||
|
3 |
2x x |
2 |
|
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||
8. |
|
|
|
|
|
dx |
|
|
|
|
|
|
2 |
|
3 |
2 5x |
|
|
|
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
5 |
x 2 |
2 |
1 |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
11. |
|
|
|
|
|
|
|
|
dx |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
5 |
|
x 2 |
|
|
1 |
|||
14. |
|
|
|
|
|
1 |
|
|
|
dx |
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3 2x x |
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
17. |
|
|
|
|
xdx |
|
|
|
|
|
||
|
1 |
3x x |
2 |
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||
20. |
|
|
(1 |
x)dx |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
2x 10 |
||||||||||
|
|
|
|
|
x |
|
||||||
9. |
|
|
2x 3 3 |
dx |
|||||||
|
2x 3 |
2 |
|||||||||
|
|
||||||||||
|
|
|
|
|
|||||||
|
|
|
3 |
x |
|
1 |
2 |
4 |
|||
|
|
|
|
||||||||
|
|
|
|
3 |
|
|
|
|
|
||
12. |
|
2 |
x 1 |
dx |
|||||||
|
|
|
|||||||||
|
|
|
|
|
|
||||||
15. |
|
|
|
|
1 |
|
|
|
dx |
||
|
x |
2 |
|
2x |
|||||||
|
|
|
|
5 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
18. |
|
|
|
|
1 |
|
|
|
dx |
||
|
x |
2 |
|
2x |
|
||||||
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
21. |
|
|
(x 9)dx |
|
|
||||||
|
x |
2 |
6x 13 |
||||||||
|
|
|
|
||||||||
|
|
|
|
|
|||||||
9. ОБ ИНТЕГРАЛАХ, КОТОРЫЕ НЕ ВЫРАЖАЮТСЯ ЧЕРЕЗ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Как известно, всякая непрерывная функция имеет первообразную. В том случае, когда первообразная некоторой элемен-
тарной функции
f x
является также элементарной функцией,
то говорят, что интеграл
f x dx
“берется”, т.е. выражается
через элементарные функции. Если же интеграл не выражается через элементарные функции, то говорят, что интеграл “не берется”.
Так, например, мы уже указывали, что первообразные от дифференциальных биномов, не принадлежащие к трем рассмотренным видам, не выражаются через элементарные функции.
Приведем еще примеры “неберущихся” интегралов, кото-
рые имеют большое значение в приложениях:
Пуассона), sinx x dx (интегральный синус),
e x2 dx
cosx x
(интеграл
dx (инте-
31

гральный косинус),
dx ln x
(интегральный логарифм),
ex dx x
(интегральная показательная функция),
(интегралы Френеля), |
|
1 k |
2 |
sin |
2 |
x dx |
|
||||||
|
|
|
2 |
|
2 |
|
cos x |
dx , |
sin x |
dx |
(эллиптический интег-
рал).
Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций. Многие из этих первообразных хорошо изучены, для них составлены подробные таблицы значений для различных значений аргумента x.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Берман Г.Н. Сборник задач по курсу математического анализа. Учебное пособие / Г.Н. Берман. СПб.: Профессия, 2001.
–432 с.
2.Бугров Я.С. Высшая математика. Дифференциальное и интегральное исчисление / Я.С. Бугров, С.М. Никольский. М.: Наука, 1988. – 432 с.
3.Пискунов Н.С. Дифференциальное и интегральное исчисления: Учеб. для втузов. В 2-х т. Т. 1. / Н.С. Пискунов. М.: Интеграл-Пресс, 2001. – 416 с.
4.Письменный Д.Т. Конспект лекций по высшей математике: полный курс / Д.Т. Письменный. М.: Айрис-пресс, 2006. – 608 с.
5.Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учебное пособие для втузов. Под ред. А.В.Ефимова и Б.П. Демидовича. М.: Наука, 1986. – 464 с.
32
СОДЕРЖАНИЕ
1.Понятие неопределенного интеграла…………………………. 1
2.Таблица неопределенных интегралов……………………….....2
3.Свойства неопределенных интегралов…………………….....3 Задачи для самостоятельного решения………………………. 6
4.Интегрирование методом замены переменной………………..7
Задачи для самостоятельного решения………………………..9
5.Интегрирование по частям…………………………………….10
Задачи для самостоятельного решения………………………12
6.Интегрирование дробно-рациональных функций…………....12
6.1.Простейшие рациональные дроби и их интегрирование..12
6.2.Разложение рациональной дроби на простейшие……….15
6.3.Интегрирование любых дробно-рациональныхфункций.17 Задачи для самостоятельного решения……………………….19
7.Интегрирование тригонометрических функций……………..20 Задачи для самостоятельного решения………………………25
8.Интегрирование иррациональных функций………………….26
8.1.Дробно-линейная подстановка…………………………….26
8.2.Тригонометрические подстановки………………………...27
8.3.Интегрирование дифференциальных биномов…………...29 Задачи для самостоятельного решения………………………...30
9.Об интегралах, которые не выражаются через элементарные функции…………………………………………........................31
10.Библиографический список…………………………………..32
33
НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы по дисциплине "Математика" студентов направления 11.03.01 "Радиотехника", профиля "Радиотехнические средства передачи, приема и обработки сигналов", специальности 11.05.01 "Радиоэлектронные системы и комплексы", профиля "Радиоэлектронные системы передачи информации" очной формы обучения
Составители Бондарев Алексей Владимирович Ряжских Александр Викторович
В авторской редакции
Подписано к изданию 29.06.2016 Уч.-изд. л. 2,1.
ФГБОУ ВО "Воронежский государственный технический университет"
394026 Воронеж, Московский просп., 14
