Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 296

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

795.07 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

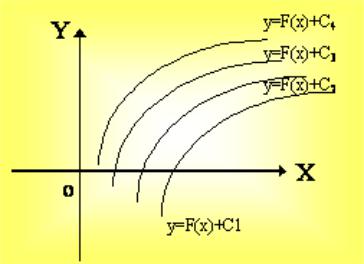
ФГБОУ ВО "Воронежский государственный технический университет"

Кафедра высшей математики и физико-математического моделирования

НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для организации самостоятельной работы по дисциплине "Математика" студентов направления 11.03.01 "Радиотехника", профиля "Радиотехнические средства передачи, приема и обработки сигналов", специальности 11.05.01 "Радиоэлектронные системы и комплексы", профиля "Радиоэлектронные системы передачи информации" очной формы обучения

Воронеж 2016

Составители: канд. физ.-мат. наук A. В. Бондарев, канд. физ.-мат. наук А.В. Ряжских УДК 517.9

Неопределенные интегралы: методические указания для организации самостоятельной работы по дисциплине "Математика" студентов направления 11.03.01 "Радиотехника", профиля "Радиотехнические средства передачи, приема и обработки сигналов", специальности 11.05.01 "Радиоэлектронные системы

икомплексы", профиля "Радиоэлектронные системы передачи информации" очной формы обучения / ФГБОУ ВО "Воронежский государственный технический университет"; сост. А.В. Бондарев, А.В. Ряжских. Воронеж, 2016. 33 с.

Методические указания содержат рекомендации по самостоятельному изучению раздела "Неопределенные интегралы" курса "Математика" и состоят из 9 параграфов. В каждом из них изложен теоретический материал по предлагаемым для самостоятельного изучения темам и разобраны типовые задачи.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего образования по направлению 11.03.01 и специальности 11.05.01, дисциплине “Математика”.

Предназначены для студентов первого курса (2 семестр). Методические указания подготовлены в электронном виде

исодержатся в файле Неопред_интегралы.pdf.

Библиогр.: 5 назв.

Рецензент канд. физ.-мат. наук, доц. Н.Б. Ускова Ответственный за выпуск зав. кафедрой д-р физ.-мат.

наук, проф. И.Л. Батаронов Издается по решению редакционно-издательского совета

Воронежского государственного технического университета

ФГБОУ ВО "Воронежский государственный технический университет", 2016

1. ПОНЯТИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА

В дифференциальном исчислении решается задача: по

данной функции	f	x		найти	ее производную. Интегральное
исчисление решает			обратную		задачу: найти функцию	F x ,
зная ее производную				x f	x .
			F
Функция F x			называется первообразной функции			f x

на отрезке

a;b , если во всех точках этого отрезка выполняется

равенство

x f

x .

(1)

Например,

первообразной функции

y x

является функция

F x

, так как

		Очевидно,			что
функции вида				F x
x	3
x			x2 .
		C
		C
3
		Теорема.		Если
функции			f x		на

первообразными будут также любые

x	3
x		C , где С – постоянная, поскольку
3		C , где С – постоянная, поскольку
3

функция	F x	является первообразной
отрезке	a;b , то множество всех

первообразных для f x задается формулой

F x C

, где С –

постоянное число.

Множество всех первообразных функций

F x C

для

функции

f x

называется неопределенным интегралом от

и обозначается		f x dx . Таким образом, по

определению


		f x dx F x C .	(2)
Здесь	f x	называется подынтегральной	функцией,
f x dx – подынтегральным выражением, x – переменной ин-

тегрирования,	– знаком неопределенного интеграла.

Операция	нахождения неопределенного	интеграла
функции называется интегрированием этой функции.
Имеет место следующая теорема. Если		функция	f

отx

непрерывна на отрезке

a;b

, то для этой функции существует

первообразная, а значит, и неопределенный интеграл.

2. ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул таблицы производных. Справедливость приведенных ниже формул легко проверить дифференцированием, т.е. установить, что производная от правой части равняется подынтегральной функции.

Интегралы в приводимой ниже таблице называются табличными. Их следует знать наизусть. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения первообразных сводятся к указанию приемов, приводящих искомый интеграл к табличному. Следовательно, необходимо знать табличные интегралы и уметь их узнавать.

xa 1

1. xa dx a 1 C , (

3. ax dx ax C . ln a

2.dxx ln x C .

4.ex dx ex C .

5.		sin x dx cos x C

7.		tg x dx ln cos x

9.		dx			tg x C .
		cos	2	x


11.		dx			arctg x C
	1 x
				2

cos x dx sin x C

ctg x dx ln sin x C

10.

ctg x C .

sin

12.

arctg

13.

15.



		dx		arcsin x
	1 x			arcsin x
	1 x			2
				2
		dx			1	ln	a
a	2	x	2		2a	ln	a
	2		2

	C
	x
	x

14.

16.



		dx			arcsin		x	C .
a			x				a
		2			2

	dx				ln x	x	2	a	2	C

x	2	a		2

В таблице производных нет формул, соответствующих формулам 7, 8, 12, 14, 15 и 16. Однако их справедливость также

легко устанавливается с помощью дифференцирования.
Например,		в	случае	формулы	(7)	имеем:
	sin x		tg x .
ln cos x		cos x	tg x .
		cos x

Следовательно,		tg x dx ln cos x C .

3.СВОЙСТВА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

1.Производная от неопределенного интеграла равна

подынтегральной функции, т.е. если

F x

, то


f x dx
f x dx	F x C	f x .	(3)

Благодаря этому свойству правильность интегрирования проверяется дифференцированием. Например, равенство

3x2 4 dx x3 4x C верно, так как x3 4x C 3x2 4 .

2. Дифференциал от неопределенного подынтегральному выражению:

d f x dx f x dx

интеграла

равен

(4)

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

dF x

F x C

(5)

Справедливость последнего равенства легко проверить дифференцированием (дифференциалы от обеих частей равенс-

тва равны dF x ).

4. Постоянный множитель можно выносить за знак интеграла:

a f x dx a f x dx ,

const

(6)

5. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций:

f x g x dx

x dx g x dx

(7)

Для доказательства найдем производные от левой и правой частей этого равенства. Они равны одному и тому же выраже-

нию

f x g x

6. Если		f

x dxf

Fax



	x C
	dx	1
		a

, то F ax C

(8)

Действительно, дифференцируя равенства (8), получим:


f ax dx	f

левую и правую части

ax ,

1		1
1		1	F ax a F ax
	F ax		F ax a F ax
a		a

Производные от правой и левой частей равны, доказать.

7. Если	f x dx F x C , то
7. Если	f x dx F x C , то

	f x b dx	F x b C .
8. Если	f x dx F x C , то
8. Если	f x dx F x C , то
	f ax b dx	1	F ax b C
	f ax b dx	a	F ax b C
		a

f ax .

что и требовалось

(9)

. (10)

Равенства (9) и (10) также доказываются дифференцирова-

нием правой и левой частей равенств.
9. Инвариантность	формулы интегрирования. Если
f x dx F x C , то и	f u du F u C , где	u x	–

произвольная функция, имеющая непрерывную производную. Таким образом, формула для неопределенно интеграла

остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.

x2dx

Например, из формулы

C путем замены x на

x получаем

C . В частности,

sin

x d

sin x

C ,

ln2 x d ln x

C .

Пример 1.

	2x	3	3sin x 5		x	dx		3	dx				3sin x dx		5	x dx
								2x
								1			x	3 1
2		x3dx 3		sin x dx		5	x 2 dx		2					cos x
										3 1
													3

			1		1
		x	2		1				1										10
		x							1			4							10

5						C				x			3cos x									x	x C.
5		1				C			2	x			3cos x							3		x	x C.
		1		1					2											3
		2		1
		2
				Пример 2.
	cos			2		x dx		1 cos 2x							dx			1				dx			cos 2


												2						2
												2						2
				Пример 3.									dx		ln				x 3				C .
				Пример 3.							x				ln				x 3				C .
											x			3
				Пример 4.									cos 7x dx							1		sin 7x C .
																				7


				Пример 5.									sin 2x				6		dx					1	cos
																								2


				Пример 6.
						dx															1 2x 3					4
						dx					2x 3					5	dx				1 2x 3
		2x 3					5														2			4



				Пример 7.										dx				2						dx		2
																		2								2

													1 25x										1		5x

x dx	1		sin 2x
	2	x	2

2x 6 C .
C			1
C			8 2x 3		4
					4

	1	arcsin 5x		C .
	5	arcsin 5x		C .
	5

Задачи для самостоятельного решения

1.
1.

4.
4.

4x				6				1		dx
4x			x		4			1		dx
					4

	1
	1			4			3
						x			dx
3
3		x
		x

			2	2				1					2		2				1
2.	3x								dx	3.	3x									dx
2.	3x			x	3			7	dx	3.	3x				x	3			7	dx
				x				7							x				7
	1															1
	1			3			2				5			3		1
5.						x		dx		6.		x						dx
															4
		x													4
		x															x

7.

10.
13.

16.

19.

5x 4		5	dx
5x 4			dx
1				dx



	15 x2
cos 3x 5 dx

1 dx cos2 3x

	1			dx


	9 x2
	9 x2

8.		1	dx
	3x 7


11.	3	1	dx
	3

		7 5x
14.		x
	sin		1 dx
	sin		1 dx
		3

17. e2 3x dx

20.		1		dx
	2x	2	8


9.	4	2x		5dx
9.		2x		5dx
12.					1		dx


		3	3x			5	2
			3x			5

15.					1			dx
					x

		sin		2
		sin				1
					5
18. 32 4 x dx
21.				1			dx
		3x	2		27

4. ИНТЕГРИРОВАНИЕ МЕТОДОМ ЗАМЕНЫ ПЕРЕМЕННОЙ

Пусть требуется найти интеграл

x dx

Сделаем

замену переменной в подынтегральном выражении, положив

x t , где t	– функция, имеющая непрерывную производ-
	t dt . На основании свойства инвариантности
ную. Тогда dx	t dt . На основании свойства инвариантности

формулы интегрирования получаем формулу замены перемен-

ной в неопределенном интеграле:
	f x dx		t dt .	(11)
		f t

После нахождения интеграла в правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной x.

Иногда целесообразно подбирать подстановку в виде t x , тогда


x x dx

t dt

(12)

Другими словами, формулу (11) можно применять справа налево.

Приведем несколько примеров на интегрирование с помощью замены переменных.

Пример 1.

Найти

sin x cos x dx .

Сделаем подстановку

t sin x , тогда dt cos x dx

. Следовательно,

sin x cos x dx

t dt

sin

x C.

Пример 2. tg x dx

sin x dx

d cos x

ln cos x C

cos x

Пример 3. Найти

x dx

Сделаем подстановку t 1 x2 ,

тогда

dt 2x dx ,

x dx

dt . Следовательно,

x dx

1 dt

1 x

ln 1 x2

Пример 4.

Найти

dx .

Сделаем

подстановку

a sin t , тогда	dx a cos t dt , t arcsin	x	. Следовательно,
		a

sin

t a cos t dt a

cos

t dt

1 cos 2t

sin 2t

arcsin

sin

2 arcsin

arcsin

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022782.86 Кб3Методическое пособие 291.pdf
#
30.04.2022784.93 Кб4Методическое пособие 292.pdf
#
30.04.2022790.13 Кб3Методическое пособие 293.pdf
#
30.04.2022794.4 Кб2Методическое пособие 294.pdf
#
30.04.2022794.89 Кб4Методическое пособие 295.pdf
#
30.04.2022795.07 Кб2Методическое пособие 296.pdf
#
30.04.2022795.19 Кб7Методическое пособие 297.pdf
#
30.04.2022799.82 Кб3Методическое пособие 298.pdf
#
30.04.2022805.01 Кб10Методическое пособие 299.pdf
#
30.04.20221.44 Mб2Методическое пособие 3.doc
#
30.04.2022157.85 Кб3Методическое пособие 3.pdf

			2	2				1					2		2				1
2.	3x								dx	3.	3x									dx
2.	3x			x	3			7	dx	3.	3x				x	3			7	dx
				x				7							x				7
	1															1
	1			3			2				5			3		1
5.						x		dx		6.		x						dx
															4
		x													4
		x															x

			2	2				1					2		2				1
2.	3x								dx	3.	3x									dx
2.	3x			x	3			7	dx	3.	3x				x	3			7	dx
				x				7							x				7
	1															1
	1			3			2				5			3		1
5.						x		dx		6.		x						dx
															4
		x													4
		x															x

			2	2				1					2		2				1
2.	3x								dx	3.	3x									dx
2.	3x			x	3			7	dx	3.	3x				x	3			7	dx
				x				7							x				7
	1															1
	1			3			2				5			3		1
5.						x		dx		6.		x						dx
															4
		x													4
		x															x