6. Динамическое программирование
Литература: [1, 6, 9, 11].
Содержание раздела
1. Общая постановка задачи динамического программирования.
2. Последовательный анализ вариантов.
3. Принцип оптимальности и уравнения Беллмана.
4. Задача об оптимальном распределении ресурсов.
5. Задача о замене оборудования.
6. Решение задачи о ранце с использованием табличной схемы динамического программирования.
7. Решение задачи о ранце с использованием рекуррентных соотношений динамического программирования.
8. Решение задачи коммивояжера с использованием рекуррентных соотношений динамического программирования.
Теоретические сведения
Задача динамического программирования (ДП) формулируется следующим образом: найти минимум (максимум) функции
(1)
при ограничениях
(2)
Эта
задача имеет следующую геометрическую
интерпретацию. Введем семейство прямых,
каждая из которых соответствует
переменной
(рис.).
Теперь
задача минимизации аддитивной функции
свелась к поиску ломаной кратчайшей
длины, соединяющей прямые
и
.
Каждая дуга этой ломаной, соединяющей
некоторые точки
,
,
представляет собой одно из слагаемых
в сумме (1). Идея метода динамического
программирования и более общего метода
последовательного анализа вариантов
состоит в возможности минимизировать
не всю сумму (2) по всем переменным, а
только пару слагаемых из нее по одной
переменной. Цена за эту возможность -
необходимость ее решения n+1
раз.
Другая
интерпретация метода динамического
программирования состоит в возможности
находить оптимальные решения в задачах
минимизации функционалов вида
,
встречающихся
в теории оптимального управления. Для
них Р. Беллманом был разработан метод
динамического программирования.
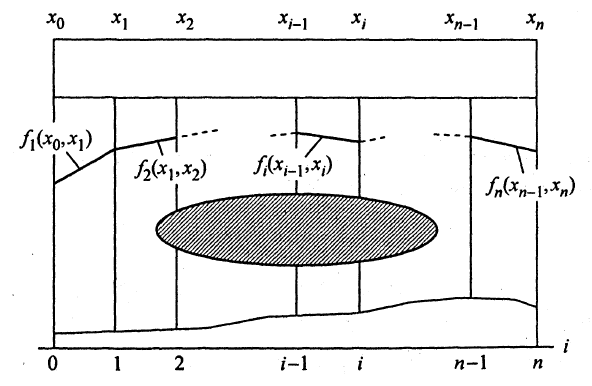
Рис. Геометрическая интерпретация задачи
динамического программирования
В
дискретном варианте интервал
интегрирования разбивается на N
шагов с
достаточно малым интервалом
,
дискретным временем
,
и величина
интеграла может быть представлена
формулой трапеций в виде
что
представляет собой аддитивную функцию
от переменных
.
Последовательный анализ вариантов. На первом шаге найдем кратчайшее расстояние от прямой до произвольной точки на прямой :
(3)
На
втором шаге отыщем кратчайшее расстояние
от прямой
до произвольной точки
на прямой
:
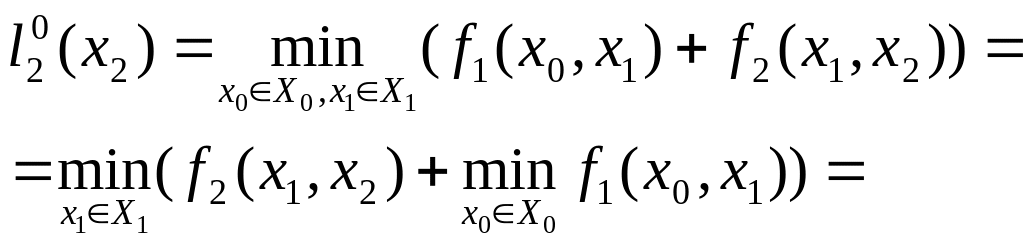
Разделение
операции минимизации на две операции
по одной переменной возможно ввиду
независимости
от
.
В этом случае
можно вынести
за знак операции минимизации по
переменной
.
Для
произвольного шага
получим аналогичным образом
Эта
рекуррентная формула вместе с начальным
условием (3) позволяет определить на
последнем шаге расчетов в прямом
направлении кратчайшее расстояние
от
начальной
прямой до произвольной точки на конечной
прямой.
Далее
расчет ведется в обратном направлении.
Сначала определим конкретную точку на
прямой
из условия
Оптимальное
значение
представляет
собой конечную точку оптимальной
траектории. Далее используем предпоследнюю
функцию
и
определяем значение
из этого
условия. Продолжая подобным образом,
восстановим всю оптимальную траекторию,
заканчивая определением точки
,
В некоторых
случаях фиксированы начальная и (или)
конечная точки, что соответствует
вырождению множеств допустимых стратегий
для этих переменных в точку.
Динамическое программирование является эффективным способом решения задач оптимального управления. В непрерывном случае оно используется сравнительно редко ввиду сложности решения уравнения Беллмана в частных производных, осложненных операцией максимизации. Применительно к дискретным многошаговым процессам уравнение Беллмана позволяет вместо оптимизации функции по всем переменным оптимизировать по шагам функцию одной переменной. Это требует меньшего количества операций по сравнению с прямой оптимизацией функции, но расходует больше памяти ЭВМ для хранения промежуточных результатов - функций Беллмана.