7.2.1. Замена неизвестной
Если в уравнении тригонометрические функции удается выразить через одну функцию, то эту функцию можно выбрать в качестве новой неизвестной.
Пример 7.8. Решить уравнение 5-7 sin x = 3cos2 x.
Используя основные тригонометрические тождества, выразим cos2 x = 1 - sin2 x и запишем уравнение в виде
5 - 7sin x = 3(1- cos2 x)
или
5-7sin x = 3 - 3 sin2 x
или
3sin2 x -7sin x + 2 = 0.
Выведем новую неизвестную y = sin x и получим квадратное уравнение
3y2 - 7y + 2 = 0,
корни которого
y1=1/3 и
y2=2.
Вернемся к старой неизвестной x.
Получаем простейшее тригонометрическое
уравнение. Его решение
,
k
.
Пример 7.9. Решить уравнение 2sin x + 5 cos x =0.
Данное уравнение является однородным уравнением первой степени. Проверим, что cos x = 0 не удовлетворяет уравнению. При постановке cos x = 0 в уравнении получаем 2sin x = 0 или sin x = 0. Но, если cos x = 0 u sin x =0, то не выполняется основное тригонометрическое тождество. Следовательно, таких значении x не существует.
Разделим все члены уравнения на cos x (т.к .cos x ≠ 0):
2tg x + 5 = 0.
Получаем простейшее
тригонометрическое уравнение tg x =
- 5/2,
его решение x = -arctg5/2
+ πk ,
k
.
Здесь учтено, что функция арктангенс −
нечетная.
Пример 7.10. Решить уравнение 2sin2 x + 5sin x cos x + 5cos2 x = 1.
Левая часть уравнения представляет собой однородный многочлен второй степени про переменным sin x и cos x. Однако в правой части уравнения стоит число 1. Поэтому, используется основное тригонометрическое тождество, запишем число 1 также в виде однородного многочлена второй степени:
1 = sin2x + cos2x.
Получаем уравнение:
2sin2 x + 5sin xcos x + 5cos2x = sin2x +cos2 x
или
sin2x + +5sin xcos x + 4cos2x = 0.
Такое уравнение является однородным.
Можно проверить, что значение cos = 0 не удовлетворяет этому уравнению. Разделим все члены уравнения на cos2x (т.к. cos х≠ 0). Имеем:
tg2x + 5tg x + 4 = 0.
Введем новую неизвестную y = tg x и получим квадратное уравнение
y2 + 5y + 4 = 0,
корни которого y1 = -1и y2 = -4. Вернемся к старой неизвестной x. Имеем простейшее тригонометрическое уравнения: tg x = -1 (его решения x = arctg (-1) + πk = -π/4 + πk, k ) и tg x = -4 (решения x = -arctg4 + πk, k ).
Пример
7.11. Решить уравнение
.
Тригонометрические
уравнения вида
с помощью подстановки
приводится к рациональному относительно
t уравнению.
Сделаем замену
.
Отсюда
.
Получаем уравнение
.
,
.
нет решений.
7.2.2. Понижение степени
Пример7.12.Решить
уравнение
.
Воспользуемся формулами понижения степени. Получаем уравнение
.
Или
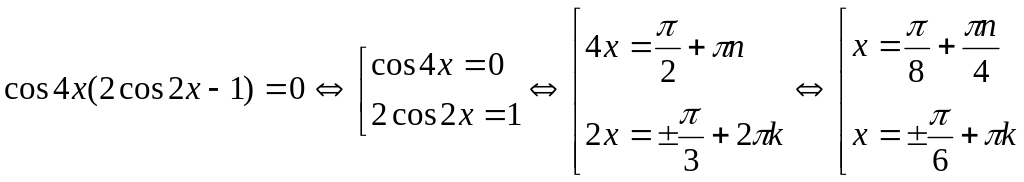
(n и k − целые числа).
7.2.3.Введение вспомогательного угла
Этот способ основан на использовании формул для синуса или косинуса суммы (разности) двух углов. Он применяется при решении уравнений a sin x + cos x = c (где a,b,c –некоторые коэффициенты ).
Разделим обе части
уравнения на 
и получим :
cos x =
.
Так как выполнены
условия 
и 
+
=
1, то можно считать 
и
= sin
(или наоборот). Из этих соотношений можно
найти угол 
.
Тогда уравнение имеет вид: 
или 
.
Это уравнение является пройстейшим и
имеет решения только при 
.
Пример 7.13.
Решить уравнение sin x + 
Найдем 
и разделим все члены уравнения на 2.
Получаем:
, будем считать что cos
= 
, sin
, тогда
=
. Уравнение имеет вид :
или
sin
=
.
Решения уравнения
x +
= 
, откуда x = 
,
где 
.
Пример 7.14.
Решить уравнение sin 10x
+ cos 10x
=
sin 16x.
Преобразуем левую
часть уравнения. Вычислим 
и
разделим все члены уравнения на
. Получаем : 
Будем считать, что cos
=
и sin
=
, тогда
= 
.
Уравнение принимает вид :
sin 
или
sin
Преобразуем разность синусов в произведение :
.
Произведение множителей равно нулю, если один из них равен нулю. Получаем
а) x
= 
n,
n
.
б)
,
.