5.1. Задачи на движение
Принятые
обозначения: расстояние – S,
L; скорости тел –
u, w,
… или 
,
,
…; время движения – t,
T.
Обычно в качестве неизвестных выбирают расстояние и скорости движущихся тел. Время в качестве неизвестного выбирается достаточно редко, так как в этом случае запись условий задачи получается громоздкой.
5.1.1. Равномерное движение по прямой
Напомним следующие часто использующиеся при решении задач, допущения.
Движение на отдельных участках считается равномерным, и пройденный путь определяется соотношением – S=vt.
При движении тела по течению реки, его скорость относительно берега w слагается из скорости тела в стоячей воде (собственной скорости) u и скорость течения реки v: w=u+v; при движении против течения: w=u-v. Тела, не имеющие двигателей (плот, бревно и т. д.), обладают скоростью течения реки: w=v.
В задачах со встречами тел: при движении тел на встречу друг другу они встречаются через время
( где S – начальное расстояние между телами; и –скорости тел); при движении тел в одну сторону ( > ) они встречаются через время
(первое тело догоняет второе).
Пример 5.1. Из пункта А в 12 ч вышел поезд. В 14 ч в том же направлении вышел другой поезд. Он нагнал первый поезд в 20 ч. Найти скорости поездов, если при одновременном движении навстречу друг другу из городов, расстояние между которыми 420 км, эти поезда встречаются через 6 ч.
Пусть скорость
первого поезда -
,
скорость второго -
,
>
.
До отправления второго поезда первый
находился в пути 2 ч и прошел за это время
,
(км). К началу движения второго поезда,
расстояние между поездами составляло
.
Так как второй поезд нагнал первый в
20 ч (т.е. через 6 ч после начала движения),
то имеем уравнение
.
При движении навстречу друг другу при расстоянии 420 км поезда встречаются также через 6 ч. Поэтому получаем уравнение
.
Итак имеем систему уравнений
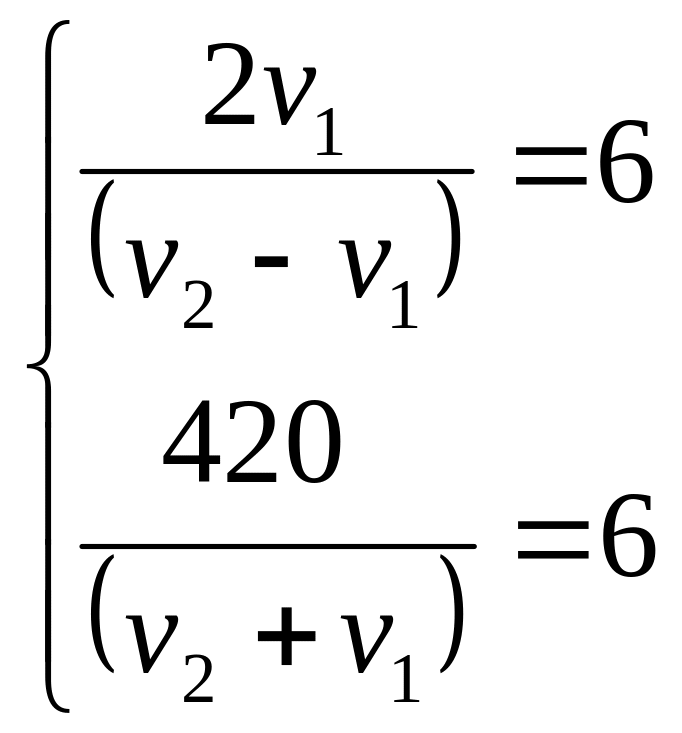
Или
.
Решив эту линейную систему уравнений, найдем: =30 км/ч, =40 км/ч.
Для наглядности
рекомендуем сопровождать задачи
рисунками, схемами, диаграммами и т. д.
На рисунке изображены условия первой
встречи поездов. Сначала из пункта А
выезжает первый поезд со скоростью .
Через два часа первый поезд находится
в точке В (на расстоянии АВ=2
,
от пункта А) и в этот момент из пункта А
выезжает второй поезд со скоростью . В
пункте С второй поезд догоняет первый
и это происходит через 6 ч после выхода
второго поезда.
А (12ч)
С
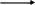В
(20ч)
(14ч)
На следующем рисунке изображены условия второй встречи поездов. Теперь поезда выходят одновременно из пунктов D и Е (с теми же скоростями что и раньше) навстречу друг другу. Расстояние DE=420 км и встреча происходит в пункте F через 6 часов после начала движения.
D
Е
F
420
км
После этих рисунков составленные уравнения становятся более наглядными.
5.1.2. Движение по окружности с постоянной скоростью
Пример 5.2. Два тела движутся по окружности равномерно в одну сторону. Первое тело проходит окружность на 2 с быстрее второго и догоняет второе тело каждые 12 с. За какое время каждое тело проходит окружность?
Пусть длина
окружности S и скорости
тел
и
(
>
).
Тогда время прохождения окружности
первым телом
,
вторым –
. Так как первое тело проходит окружность
на 2 с быстрее второго, то имеем уравнение:
. Кроме того, известно, что первое тело
догоняет второе каждые 12 с. Поэтому
запишем уравнение
.
По условию задачи надо найти времена и . Из второго уравнения имеем
.
Подставив в первое уравнение, получим
.
Сократив все члены уравнения на 2, и разделив дроби почленно, имеем:
.
Введя замену
неизвестной
,
получим квадратное уравнение: , корни
которого
и
.
Тогда
. Отсюда первое тело проходит
окружность за 4 с, второе – за 6 с.