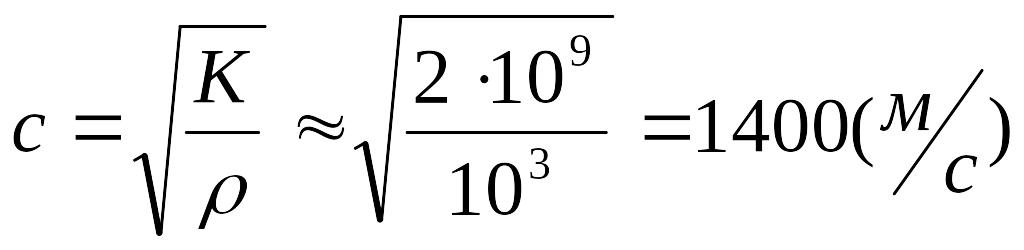- •Механические колебания. Упругие волны методические указания
- •Предисловие
- •Механические колебания
- •1.1. Гармонические колебания
- •1.2. Энергия гармонического колебания
- •1.3. Маятники
- •1.4. Сложение колебаний одного направления
- •1.5. Сложение взаимно перпендикулярных колебаний
- •1.6. Затухающие колебания
- •Основные характеристики затухающих колебаний:
- •1.7. Вынужденные колебания. Резонанс
- •1.8. Примеры
- •1.9. Задачи
- •2. Упругие волны
- •2.1. Основные понятия. Уравнение волны
- •2.2. Скорость волны в твердых телах
- •2.3. Скорость звука в жидкостях и газах
- •2.4. Энергия упругой волны
- •Отражение и прохождение упругих волн на границе раздела двух сред
- •Стоячие волны
- •2.7. Колебания струны
- •2.8. Акустический эффект Доплера
- •2.9. Примеры
- •2.10. Задачи
- •Библиографический список
- •Содержание
- •Механические колебания. Упругие волны методические указания
- •394026 Воронеж, Московский просп., 14
2.2. Скорость волны в твердых телах
При распространении упругих волн происходит деформация среды. При продольных волнах - деформация растяжения и сжатия, при поперечных – сдвига. Если деформировать (сжать, растянуть или сдвинуть относительно друг друга) крайние точки тела, то эта деформация будет распространяться в теле с некоторой скоростью . Для вычисления величины рассмотрим простейший случай передачи деформации через упругий стержень.
Пусть в течение короткого промежутка времени t ударом молотка мы сообщим этому стержню некоторый импульс. За это время точки торца стержня сместятся на некоторое расстояние l. Возникшая деформация будет перемещаться от точки к точке, и по стержню побежит волна сжатия. К концу промежутка времени t все частицы участка стержня длины l, вовлеченного в колебательный процесс, будут двигаться со скоростью υ = l/t вправо. Поскольку в начале этого промежутка частицы были неподвижны, то приращение количества движения стержня будет равно mu – 0, где m – масса участка l. Обозначив площадь поперечного сечения стержня через S, а плотность материала стержня через , мы получим dm = Sl. По второму закону Ньютона приращение количества движения равно импульсу внешней силы F, действовавшей при ударе на стержень, т.е.
Ft
=
![]() Sl.
С
другой стороны, по закону Гука имеем F
= ESΔl/l,
где
Е
– модуль Юнга. Исключив из этих уравнений
силу F,
сначала получим
Sl.
С
другой стороны, по закону Гука имеем F
= ESΔl/l,
где
Е
– модуль Юнга. Исключив из этих уравнений
силу F,
сначала получим
![]() ,
а
затем
,
а
затем
![]() .
Отсюда
скорость распространения волны сжатия
(продольной волны) в упругом стержне
равна
.
Отсюда
скорость распространения волны сжатия
(продольной волны) в упругом стержне
равна
![]() .
(51)
.
(51)
Подобные расчеты скорости поперечных волн дают
![]() .
(52)
.
(52)
где G – модуль сдвига среды.
Выражение
![]() называется волновым сопротивлением
или импедансом среды.
называется волновым сопротивлением
или импедансом среды.
2.3. Скорость звука в жидкостях и газах
Без доказательства согласимся с тем, что скорость упругих волн в жидкостях и газах равна
с
=
![]() ,
(53)
,
(53)
где
К
– модуль объемной упругости,
![]() - плотность невозмущенной среды. Модуль
объемной упругости для определенной
жидкости или реального газа находится
экспериментально. Для идеального газа
K
=
p,
где p
– давление невозмущенного газа,
–
показатель адиабаты. Этот результат
легко получить, если процесс объемной
деформации жидкости или газа при
распространении в них звуковых волн
считать адиабатным. Уравнение адиабаты
для идеального газа имеет вид
- плотность невозмущенной среды. Модуль
объемной упругости для определенной
жидкости или реального газа находится
экспериментально. Для идеального газа
K
=
p,
где p
– давление невозмущенного газа,
–
показатель адиабаты. Этот результат
легко получить, если процесс объемной
деформации жидкости или газа при
распространении в них звуковых волн
считать адиабатным. Уравнение адиабаты
для идеального газа имеет вид
![]() ,
,
![]() (54)
(54)
где
V
– объём газа;
![]() – показатель адиабаты, равный отношению
теплоёмкостей газа Ср/Сv:
Ср
– теплоёмкость газа при постоянном
давлении, Сv
– при постоянном объёме. Возьмём
дифференциалы от обеих частей равенства
(54)
– показатель адиабаты, равный отношению
теплоёмкостей газа Ср/Сv:
Ср
– теплоёмкость газа при постоянном
давлении, Сv
– при постоянном объёме. Возьмём
дифференциалы от обеих частей равенства
(54)
![]()
Отсюда
получим
![]() или
в конечных разностях
или
в конечных разностях
![]() (55)
(55)
Здесь
(-![]() )
представляет собой силу объёмной
упругости газа, действующей на единицу
площади поверхности сосуда и по сути
аналогична нормальному напряжению
)
представляет собой силу объёмной
упругости газа, действующей на единицу
площади поверхности сосуда и по сути
аналогична нормальному напряжению
![]() ;
величина
;
величина ![]() приобретает смысл относительной
всесторонней деформации.
приобретает смысл относительной
всесторонней деформации.
На основании этих замечаний равенство (55) принимает форму закона Гука
![]() где
K
=
p
где
K
=
p
Если учесть, что плотность идеального газа равна
![]()
где М – молярная масса, R – газовая постоянная и T – абсолютная температура, то для скорости звука в идеальном газе получим
![]() (56)
(56)
При нормальных условиях (p = 105 Па, Т = 300 К) атмосферный воздух по своим свойствам подобен идеальному газу. Отсюда получим оценку скорости звука в воздухе, для которого
![]() ;
;
![]() .
.
Для
воды
![]() ,
= 103
кг/м3
скорость звука
,
= 103
кг/м3
скорость звука
.