1.6. Затухающие колебания

Р ассмотрим колебания механической системы в условиях действия сил сопротивления. Как показывает опыт, в первом приближении сила сопротивления пропорциональна скорости колеблющейся частицы. Тогда закон движения частицы запишется в виде:

m =-kx– r , (23)

где r – коэффициент сопротивления; k – коэффициент упругости, характеризу­ющий возвращающую силу.

Уравнение (23) может быть приведено к стандартному виду, представляющему дифференциальное уравнение затухающих колебаний

+ 2β + ₀²x = 0, (24)

где β = r/2m –коэффициент затухания; ₀ = - собственная частота колебаний системы. Решение уравнения (24) имеет вид

x = A₀ e^{- βt} cos(t + α), (25)

где  = - частота затухающих колебаний.

График функции (25) показан на рис.9. Амплитуда затухающих колебаний убывает по закону

А = А₀e^{- βt} (26)

Период затухающих колебаний равен

Т = 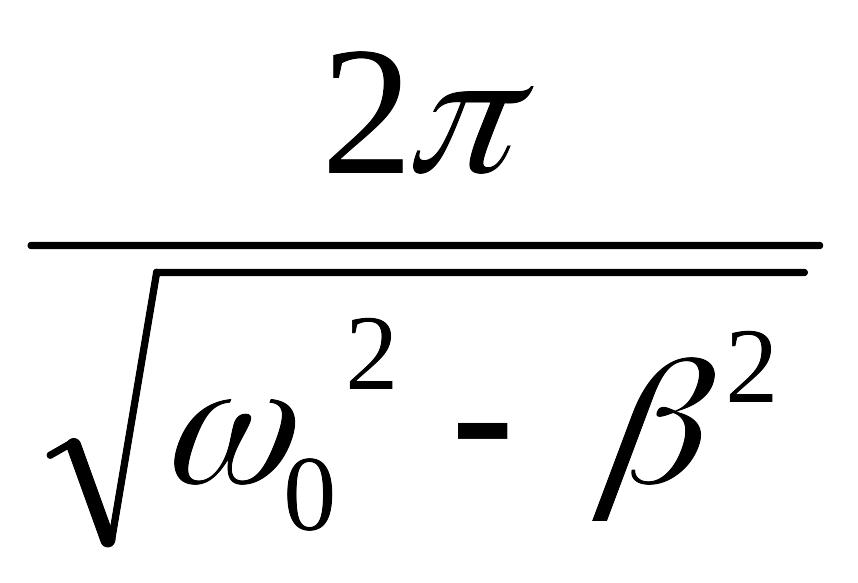(27)

где ₀= .

С ростом коэффициента затухания β период затухающих колебаний увеличивается, стремясь к бесконечности при критическом коэффициенте затухания β_кр = ₀. При β  β_кр процесс носит апериодический характер. Выведенная из положения равновесия система возвращается к нему, не совершая колебаний (рис.10).

Основные характеристики затухающих колебаний:

1) время релаксации  - время, в течение которого амплитуда уменьшается в е раз:

(28)

отсюда  = 1/β;

2) логарифмический декремент затухания λ, представляет натуральный логарифм отношения двух соседних амплитуд, т.е.

, (29)

где N – число колебаний, совершаемых за время релаксации; T-период колебаний.

3) добротность колебательной системы

, (30)

где Е – энергия системы в момент времени t; ∆Е – убыль энергии за следующий период колебаний.

1.7. Вынужденные колебания. Резонанс

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы. С учетом вынуждающей силы закон движения материальной точки запишется в виде

m = -kx – r + F₀ cos t. (31)

После преобразования получим неоднородное дифференциальное уравнение, описывающее вынужденные колебания.

+ 2β + ₀²x = ƒ₀ cos  t , (32)

где ƒ₀ = F/m.

Общее решение данного неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.

Общее решение однородного уравнения имеет вид

x₁ = A₀ e^-βtcos(t + α) , (33)

где  = , А₀ и α – произвольные постоянные.

Эти колебания достаточно быстро затухают, и вынужденные колебания будут определяться частным решением

x₂ = A cos(t – φ). (34)

Здесь А - амплитуда установившихся вынужденных колебаний. Она равна:

(35)

Величина

(36)

характеризует отставание вынужденных колебаний системы от колебаний вынуждающей силы.

С лагаемое (33) играет значительную роль на начальной стадии процесса установления колебаний. График вынужденных колебаний представлен на рис.11.

В установившемся режиме вынужденные колебания происходят с частотой вынуждающей силы, амплитуда и начальная фаза которых определяются выражениями (35) и (36).

Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При некоторой частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

Чтобы определить резонансную частоту, нужно найти максимум функции (35) или, что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по  и приравняв производную нулю, получим условие, определяющее _рез:

-4(₀²-²) +8 β²=0 (37)

Уравнение (37) имеет три решения: =0 и _рез = Решение, равное нулю, соответствует статическому состоянию системы, отрицательное не имеет смысла и отбрасывается. Таким образом, для резонансной частоты получаем одно значение

_рез = . (38)

Амплитуда колебаний при резонансе равна

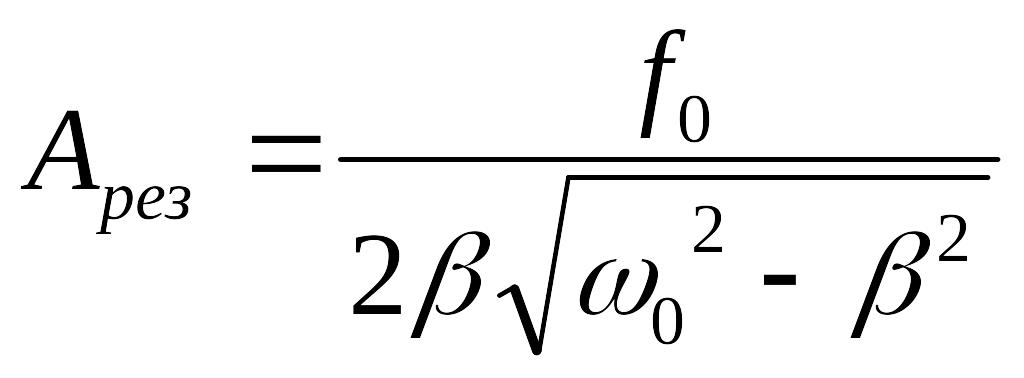(39)

Резонансные кривые при различных значениях коэффициента затухания представлены на рис.12. Чем меньше β, тем выше и правее лежит резонансный максимум.

Если  → 0, то все резонансные кривые приходят к одному и тому же значению ƒ₀/₀², так называемому статическому отклонению.

Резонансная амплитуда связана с добротностью Q колебательной системы следующим соотношением:

А_рез = (40)

Таким образом, добротность характеризует резонансные свойства колебательной системы: чем больше Q, тем острее и выше резонанс.