
- •Механические колебания. Упругие волны методические указания
- •Предисловие
- •Механические колебания
- •1.1. Гармонические колебания
- •1.2. Энергия гармонического колебания
- •1.3. Маятники
- •1.4. Сложение колебаний одного направления
- •1.5. Сложение взаимно перпендикулярных колебаний
- •1.6. Затухающие колебания
- •Основные характеристики затухающих колебаний:
- •1.7. Вынужденные колебания. Резонанс
- •1.8. Примеры
- •1.9. Задачи
- •2. Упругие волны
- •2.1. Основные понятия. Уравнение волны
- •2.2. Скорость волны в твердых телах
- •2.3. Скорость звука в жидкостях и газах
- •2.4. Энергия упругой волны
- •Отражение и прохождение упругих волн на границе раздела двух сред
- •Стоячие волны
- •2.7. Колебания струны
- •2.8. Акустический эффект Доплера
- •2.9. Примеры
- •2.10. Задачи
- •Библиографический список
- •Содержание
- •Механические колебания. Упругие волны методические указания
- •394026 Воронеж, Московский просп., 14
1.4. Сложение колебаний одного направления
Воспользуемся представлением гармонического колебания моделью вращающегося вектора амплитуды (рис.4).
|
|
Рис.4 |
Рис.5 |
Введем ось Х и из точки О, взятой на этой оси, отложим вектор длины А, образующий с осью угол . Если привести вектор А во вращение с угловой скоростью 0, то проекция этого вектора на ось х будет изменяться со временем по закону x = A cos (0t+о). Следовательно, гармоническое колебание может быть задано с помощью вектора амплитуды. Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты:
x1=А1cos(0t+1), x2= A2cos(0t+2) (17)
Представим
оба колебания с помощью векторов ![]() (рис.5). Построим по правилу сложения
векторов результирующий вектор
(рис.5). Построим по правилу сложения
векторов результирующий вектор ![]() .
Проекция этого вектора на ось х
равна сумме проекций слагаемых векторов:
x
= x1+x2
.
Проекция этого вектора на ось х
равна сумме проекций слагаемых векторов:
x
= x1+x2
Вектор будет характеризовать результирующее колебание. Этот вектор вращается с той же угловой скоростью 0, как и векторы , так что результирующее движение будет гармоническим колебанием частотой 0 и определяемыми значениями амплитуды А и начальной фазой . Из рис.5. видно, что
A2 = A12+A22+2A1A2 cos(2-1) (18)
![]() (19)
(19)
1.5. Сложение взаимно перпендикулярных колебаний
Пусть материальная точка совершает колебания в двух взаимно перпендикулярных направлениях, например, вдоль координатных осей Х и У. Уравнения соответствующих колебаний при этом будут следующими
x = а cost, y = b cos(t+) (20)
Уравнения (20) в параметрической форме задают траекторию, по которой движется тело. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (20) параметр t (время). Проделаем несложные математические преобразования, представляя:
cost
=![]() ;
sint
=
;
sint
=
![]() (21)
(21)
Подставляя (21) в формулу
(cos(+)=coscos-sin sin), получим:
![]() =
cost
cos-sint
sin
=
=
cost
cos-sint
sin
=
![]() cos-sin
2
;
cos-sin
2
;
- cos = -sinα ;
или, возводя в квадрат и преобразуя
![]() +
+![]() -2
-2
![]() cos
= sin2
(22)
cos
= sin2
(22)
Это и есть уравнение траектории. В общем случае – это эллипс, оси которого ориентированы произвольно относительно координатных осей Х и У. Ориентация эллипса зависит от амплитуд a и b и разности фаз . Найдем траектории в некоторых частных случаях:
Разность фаз = 0, тогда
+ -2 = 0; или ( - )2 = 0
Откуда следует, что y = bx/a для |x| a.
Т
 очка
колеблется по отрезку прямой (рис.6.),
причем, ее расстояние от начала координат
О равно
очка
колеблется по отрезку прямой (рис.6.),
причем, ее расстояние от начала координат
О равно ![]() =
=![]() .
.

П одставляя
значения х и у, получим:
одставляя
значения х и у, получим:
![]()
![]() .
.
Таким
образом, результирующее движение
является гармоническим колебанием с
частотой
и амплитудой
![]() .
.
При = из уравнения (22) получим:
+
-2
cos()
= sin2(),
или
+
-2
=
0
, т.е.
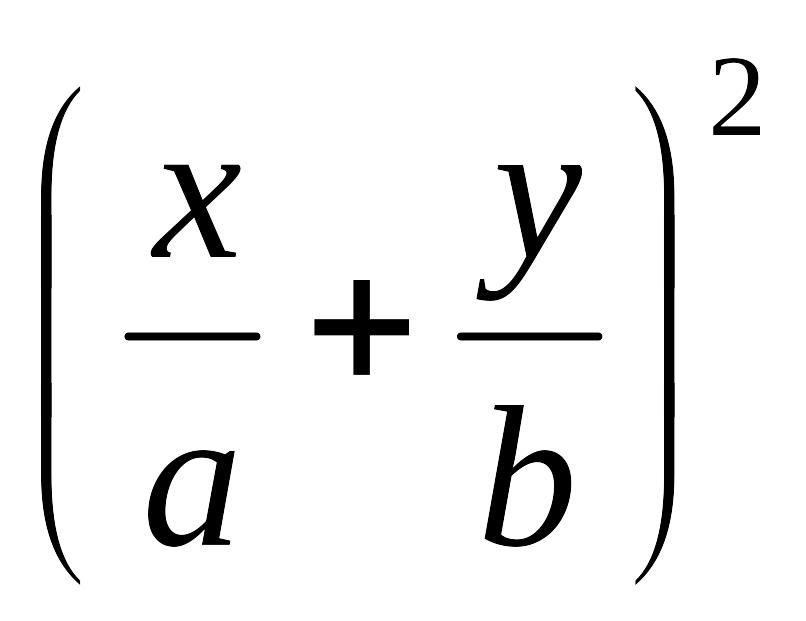 =
0. Отсюда имеем
=
0. Отсюда имеем
![]() ,
|х|
≤ a
(см.
рис.7.). И в этом случае точка колеблется
по отрезку прямой.
,
|х|
≤ a
(см.
рис.7.). И в этом случае точка колеблется
по отрезку прямой.
П

 ри
= /2
уравнение траектории точки принимает
вид
ри
= /2
уравнение траектории точки принимает
вид
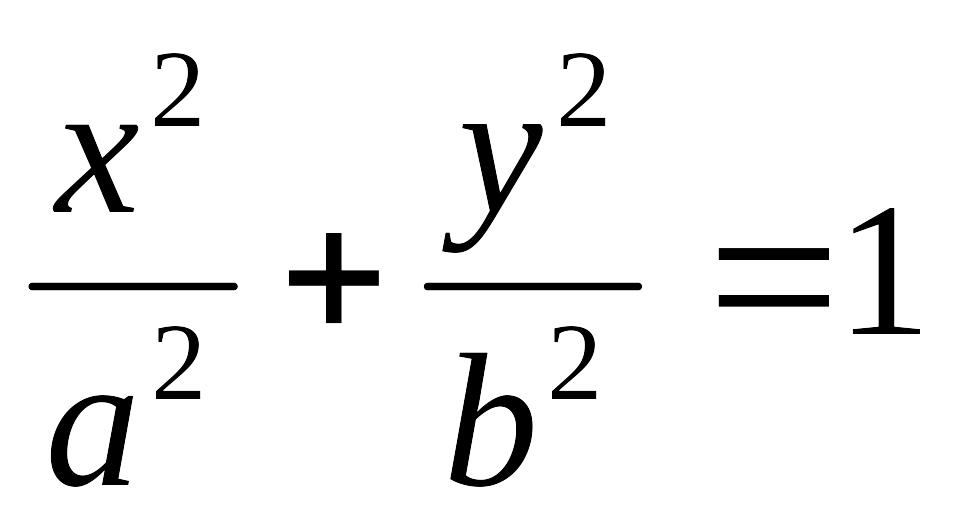 .
Это означает, что точка при своем
движении описывает эллипс.
.
Это означает, что точка при своем
движении описывает эллипс.
Когда = /2 материальная точка вращается по эллипсу по ходу часовых стрелок, а при = - /2 - в противоположном направлении. Стрелками указаны направления движения точки по эллипсу (рис.8.).


