Если при определении момента использовать выражение

, (11)

т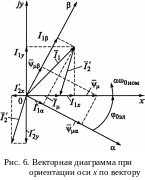 о в качестве регулируемых будут выбраны векторы и . Их векторные диаграммы при ориентации по вектору потокосцепления оси х системы координат х, у, вращающейся с синхронной скоростью поля двигателя, представлены на рис. 6. Здесь же показаны векторы токов намагничивания , ротора и проекции векторов тока статора и ротора на оси х, у, а также на оси ,  неподвижной системы координат, связанной со статором АД.

Анализ рис. 6 позволяет интерпретировать АД как эквивалентную машину постоянного тока. Если ротор АД сопоставить якорю двигателя постоянного тока (ДПТ), а статорные обмотки – обмоткам возбуждения ДПТ, то составляющая тока статора I_1x, синфазная потокосцеплению , может интерпретироваться как ток возбуждения ДПТ, составляющая I_1у – как ток его компенсационной обмотки, составляющая I_2у' – как поперечная составляющая поля якоря ДПТ, составляющая I_2х' – как размагничивающая продольная реакция якоря. Из рис. 6 видно, что потокосцепление определяется током . Следовательно, в системе координат х, у, связанной с вектором потокосцепления , составляющие I_1у и I_2у' равны и имеют разные знаки, а встречно направленные составляющие I_1x и I_2x', определяют модуль потокосцепления , где L₁₂ – взаимная индуктивность обмоток статора и ротора АД.

В приведенной интерпретации отличительные особенности АД от ДПТ состоят в том, что на статоре АД нет отдельных обмоток, эквивалентных обмотке возбуждения и обмотке, компенсирующей поперечную реакцию якоря (указанные обмотки как бы совмещены в одной обмотке статора), а ось х, связанная с вектором потокосцепления , вращается относительно статора со скоростью _0ном, где  = f₁ / f_1ном – относительная частота напряжения питания статора АД; _0ном = 2 f_1ном / p_п – синхронная угловая скорость вращения магнитного поля при номинальной частоте напряжения питания f_1ном и числе пар полюсов р_п статора АД.

Особенности формирования момента в соответствии с выражением (11) определяют основные положения при технической реализации системы векторного управления АД. Так, вектор может быть определен по его проекциям _ и _ на оси  и  (см. рис. 6): . Каждая из составляющих может быть непосредственно измерена с помощью датчиков Холла, установленных в воздушном зазоре между статором и ротором АД.

При этом модуль потокосцепления , а угол между осями ,  неподвижной системы координат и осями х, у системы координат, вращающейся со скоростью _0ном,

(12)

Составляющие вектора в системе координат ,  при условии инвариантности мощности АД в двухфазной и трехфазной системах координат могут быть определены через токи фаз статора I_1А, I_1В, I_1С:

(13)

При том же условии составляющие вектора тока в системе координат х, у

(14)

Составляющие I_1х и I_1y не зависят от частоты питания АД и по своей форме являются постоянными. С учетом этого система векторного управления строиться аналогично системам управления двигателями постоянного тока, в которых составляющая I_1х тока статора определяет потокосцепление _ АД (магнитный поток), а составляющая I_1у является моментной составляющей тока статора (подобна току якоря ДПТ).

Таким образом, система векторного управления с опорным вектором потокосцепления должна иметь два канала управления – модулем _ и угловой скоростью ротора АД. По аналогии с ДПТ канал управления скоростью содержит внутренний контур управления составляющей тока статора I_1у, эквивалентной току якоря ДПТ, и внешний контур управления угловой скоростью ротора.

Канал управления модулем потокосцепления _ должен содержать контур управления составляющей тока статора I_1х, эквивалентной току возбуждения ДПТ. Хотя по своей функции этот канал и подобен каналу управления магнитным потоком ДПТ, он более сложен, поскольку взаимосвязь модуля _, составляющих тока и напряжения статора по оси х характеризуется дифференциальными уравнениями второго порядка. На этот канал оказывает влияние и составляющая тока статора I_1у в виде трансформаторных ЭДС, пропорциональных рассеяниям статора и ротора.

Важной особенностью системы управления с опорным вектором потокосцепления является возможность его прямого измерения с помощью датчиков, установленных в воздушном зазоре АД. Подобные системы имеют более высокие показатели качества управления по сравнению с системами, где используется косвенный (расчетный) путь определения сигналов обратных связей.

Если при определении момента использовать выражение

, (15)

г де L₂' – индуктивность обмотки ротора, приведенная к цепи статора, то в качестве регулируемых будут выбраны векторы и . Их векторные диаграммы при ориентации по оси х системы координат х, у представлены на рис. 7. Здесь же показаны векторы токов намагничивания , ротора и проекции векторов тока статора и ротора на оси х, у и , .

При этом

(16)

_2х = L₁₂ I_1x + L₂ I_2x = ₂, _2у = L₁₂ I_1y + L₂ I_2y = 0,

I_2x = 0, I_2y = – ₂_0ном s_a /R₂',

т.е. в установившемся режиме вектор тока ротора отстает от вектора на угол 90 эл. град., а его модуль при ₂ = const меняется пропорционально абсолютному скольжению.

В двигательном режиме вектор тока статора опережает вектор на угол  = arctg(L₂'_0ном s_a /R₂' ), его составляющая I_1х = ₂ /L₁₂ определяет потокосцепление ротора ₂, а составляющая I_1у = ₂L₂'_0ном s_a /(L₁₂R₂' ) компенсирует влияние на него реакции ротора.

В соответствии с выражениями (15) и (16) электромагнитный момент АД определяется взаимодействием ортогональных составляющих потокосцепления ротора ₂ = _2х = L₁₂ I_1x и тока статора I_1у. Таким образом, при стабилизации , как и при стабилизации , система векторного управления будет подобна системам управления двигателями постоянного тока, где составляющая I_1x тока статора определяет потокосцепление АД (магнитный поток ДПТ), а составляющая I_1у является моментной составляющей тока статора (аналогично току якоря ДПТ).

Особенностью систем управления с опорным вектором потокосцепления ротора является более простая, чем при опорном векторе , структура управления. В соответствии с рис. 7 она должна иметь два канала управления – потокосцеплением и скоростью двигателя. Канал управления двухконтурный: внутренний контур управляет составляющей I_1х тока статора, внешний – модулем потокосцепления ротора. Двухконтурным может быть и канал управления скоростью АД: внутренний контур управляет составляющей I_1у тока статора, внешний – угловой скоростью ротора.

Недостаток систем с опорным вектором потокосцепления ротора в том, что определение этого вектора возможно лишь расчетным путем на основе параметров АД, как правило, известных не точно и изменяющихся при работе двигателя.

При стабилизации потокосцепления ротора (₂ = const) механические характеристики АД подобны характеристикам ДПТ с независимым возбуждением. Поскольку теория и технические решения замкнутых систем управления электроприводом с ДПТ, имеющим независимое возбуждение, достаточно апробированы, то понятна привлекательность применения систем векторного управления с управлением по потоку ротора.

2.2. Управление по вектору потокосцепления ротора

Динамические свойства короткозамкнутого АД при питании от источника напряжения в системе координат х, у при ориентации вектора по оси х определяются из выражений [4]:

для статорной цепи

U_1x = d_1x dt + I_1x R₁ – _0эл_1y,

(17)

U_1y = d_1y dt + I_1y R₁ + _0эл_1x,

для цепи ротора АД

0 = d_2x dt + I_2x R₂,

(18)

0 = I_2y R₂ + (_0эл – р_п)_2x = I_2y R₂ + _0эл.ном s_a_2x .

Здесь U_1x, U_1y – проекции вектора напряжения питания статора АД.

Проекции векторов потокосцеплений статора и ротора на оси х, у:

_1х = L₁ I_1x + L₁₂ I_2x, _1у = L₁I_1y + L₁₂ I_2y, (19)

_2х = L₂ I_2x + L₁₂ I_1x, _2у = 0 = L₂ I_2y + L₁₂ I_1y, (20)

Поскольку при ориентации вектора потокосцепления ротора по оси х в системе управления АД представляет интерес определение зависимостей между переменными ₂ и I₁, исключим из уравнений (17)(20) переменные _1х, _1y, I'_2х и I'_2у. Из (20) токи ротора

(21)

С учетом (21) уравнения (19) преобразуются к виду

_1х = k₂ _2х + L₁ I_1x, _1у = L₁I_1y, (22)

где k₂ = L₁₂ /L₂' – коэффициент электромагнитной связи ротора;

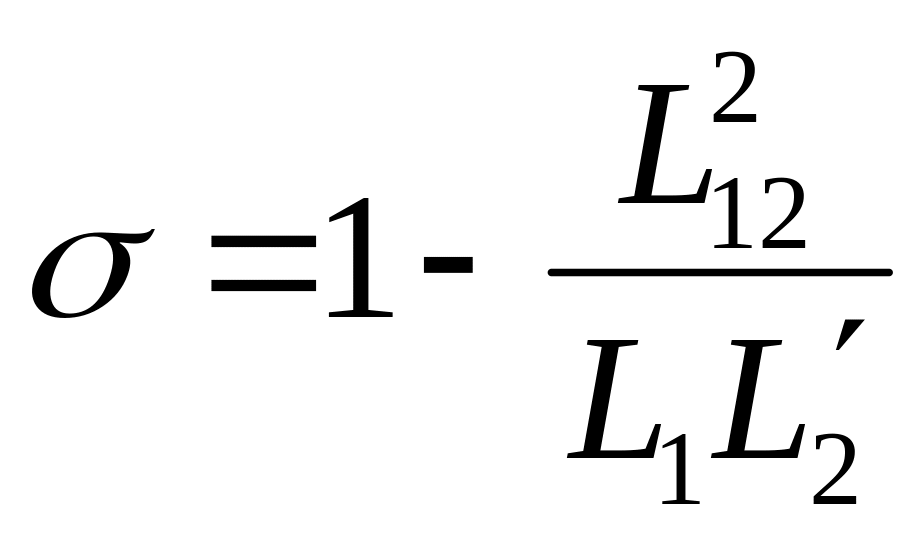– коэффициент рассеяния магнитного поля АД.

Подставив (22) в (17), для статорной цепи АД получим

(23)

Уравнения (18) для роторной цепи с учетом (21) преобразуются к виду

(24)