2.2. Фотоэффект

Пример 2.2.1.

Определить максимальную скорость v_max фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ₁=0,155 мкм; 2) γ - излучением с длиной волны λ₂=2,47 пм.

Решение.

Максимальную скорость фотоэлектронов опреде­лим из уравнения Эйнштейна для фотоэффекта:

(1)

Энергия фотона вычисляется по формуле , работа выхода А для серебра A = 4,7 эВ.

Кинетическая энергия фотоэлектрона в зависимости от того, ка­кая скорость ему сообщается, может быть выражена или по класси­ческой формуле

(2)

или по релятивистской

T = (m – m₀)c² (3)

Скорость фотоэлектрона зависит от энергии фотона, вызывающе­го фотоэффект: если энергия фотона ε много меньше энергии покоя электрона Е₀, то может быть применена формула (2); если же Е сравнима по величине с Е₀, то вычисление по формуле (2) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3).

1) В формулу энергии фотона подставим значения вели­чин и, произведя вычисления, для ультрафиолетового излу­чения получим

ε₁= 1,28 ∙ 10^-18 Дж = 8 эВ.

Его значение энергии фотона много меньше энергии покоя элек­трона (0,51 МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть вы­ражена по классической формуле (2), откуда

(4)

Выпишем величины, входящие в формулу (4):

ε₁ = 1,28 ∙ 10¹⁸ Дж (вычислено выше); А = 4,7 эВ =

= 4,7 ∙ 1,6 ∙ 10^-19 Дж = 0,75 ∙ 10^-18 Дж; m₀ = 9,11 ∙ 10^-31 кг.

Подставив числовые значения в формулу (4), найдем максималь­ную скорость:

v_max = 1,08 Мм/с.

2. Вычислим теперь энергию фотона γ - излучения:

= 8,04 фДж = 0,502 МэВ.

Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией γ - фотона. поэтому можно принять, что макси­мальная кинетическая энергия электрона равна энергии фотона:

T_max = = 0,502 МэВ.

Так как в данном случае кинетическая энергия электрона сравнима с его энергией покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии

, где E₀ = m₀c². Выполнив преобразования,

найдем

.

Сделав вычисления, получим β = 0,755.

Следовательно, максимальная скорость фотоэлектронов, вырывае­мых γ - излучением,

v_max = cβ = 226 Мм/с.

Пример 2.2.2.

Определить красную границу λ₀ фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны λ = 400 нм максимальная скорость v_max фотоэлектро­нов равна 0,65 Мм/с.

Решение.

При облучении светом, длина волны λ₀ которого соответствует красной границе фотоэффекта, скорость, а следова­тельно, и кинетическая энергия фотоэлектронов равны нулю. Поэтому уравнение Эйнштейна для фотоэффекта

ε = А+Т в случае красной границы запишется в виде

ε = А, или hc/λ₀ = A.

Отсюда

λ₀ = hc/A (1)

Работу выхода для цезия определим с помощью уравнения Эйн­штейна:

. (2)

Выпишем числовые значения величин, выразив их в СИ: h = 6,62 ∙ 10^-34 Дж ∙ с; с=3 ∙ 10⁸ м/с; λ = 400 нм=4 ∙ 10^-7 м; m = 9,11 ∙ 10^-31 кг; v = 6,5 ∙ 10⁵ м/с.

Подставив эти значения величин в формулу (2) и вычислив, получим

A = 3,05 ∙ 10^-19 Дж = 0,305 аДж.

Для определения красной границы фотоэффекта подставим значения в формулу (1) и вычислим:

λ₀ = 651 нм.

Пример 2.2.3.

На плоский алюминиевый электрод падает ультрафиолетовое излучение с длиной волны нм. На какое максимальное расстояние d от его поверхности может удалиться фотоэлектрон, если вне электрода имеется однородное электрическое поле напряженностью В/см, задерживающее этот фотоэлектрон? Красная граница фотоэффекта для алюминия нм.

нм

В/см

нм

Решение:

Из уравнения Эйнштейна для фотоэффекта:

(1)

найти кинетическую энергию фотоэлектрона , которую он имеет сразу после вылета из электрода, и приравнять ее к работе однородного электрического поля:

(2)

задерживающего электрон. Отсюда можно найти искомое расстояние d. Из выражение (1):

(3)

где и .

С учетом (4)

поскольку , то, приравняв правые части равенств (2) и (3), получим:

откуда

Произведем вычисления:

м.

Ответ: м.

Пример 2.2.4.

Поток монохроматического излучения ( мкм) падает на металлическую пластину. Фототок полностью прекращается, когда задерживающая разность потенциалов достигает 0,7 В. Найти работу выхода и красную границу фотоэффекта.

мкм

В

Решение:

Работу выхода можно определить из уравнения Эйнштейна для фотоэффекта:

(1)

где постоянная Планка; длина волны;

скорость света в вакууме;

работа выхода;

максимальная кинетическая энергия фотоэлектронов.

Так как даже самые быстрые фотоэлектроны, пролетев некоторое расстояние в тормозящем электрическом поле, полностью теряют свою начальную кинетическую энергию, можем записать:

(2)

где заряд электрона; задерживающая разность потенциалов.

Подставляя выражение (2) в (1), получим:

(3)

Откуда работа выхода равна:

(4)

Подставляя в формул (4) числовые значения получим:

Красной границе фотоэффекта в уравнение Эйнштейна (1) соответствует условие . Тогда, заменив значение на , получим

мкм.

Ответ: эВ; мкм.

Пример 2.2.5.

Средняя длина волны излучения лампы накаливания с металлической спиралью равна 1200 нм. Найти число фотонов, испускаемых за единицу времени лампой мощностью 500 Вт.

нм

Вт

Решение:

В установившемся режиме вся энергия, которая потребляется лампой накаливания, излучается металлической нитью.

Мощность теплового излучения выразим как произведение энергии одного кванта на количество квантов N, излучаемых нитью в единицу времени:

Отсюда

Ответ:

Пример 2.2.6.

Монохроматический пучок электромагнитных волн падает на тонкую платиновую фольгу, находящуюся в вакууме в однородном магнитном поле с индукцией Радиус кривизны траектории электронов, выбитых из металла в плоскости, перпендикулярной полю, оказался равным 0,01 м. Определить длину волны падающего излучения, если красная граница фотоэффекта для платины равна .

м

Решение:

Фотоны электромагнитного поля при поглощении их металлом вызывают фотоэффект, то есть выбивают из металла электроны. Энергия фотона идет на увеличение потенциальной энергии электрона:

приобретает кинетическую энергию :

(1)

Кинетическую энергию фотоэлектронов можно выразить через их импульс:

(2)

где - импульс электрона; m – масса электрона;

e – заряд электрона; B – индукция магнитного поля.

Вектор скорости фотоэлектронов перпендикулярен вектору индукции магнитного поля, поэтому они описывают окружность радиусом R.

Подставляя (2) в (1), получим:

;

отсюда нм.

Ответ: нм.

Пример 2.2.7.

Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра:

1) ультрафиолетовым излучение с длиной волны мкм; 2) излучение с длиной волны пм.

мкм

пм

эВ

Решение:

Максимальную скорость фотоэлектронов определим из уравнения Эйнштейна для фотоэффекта:

(1)

Энергия фотона вычисляется по формуле:

Кинетическая энергия фотоэлектрона в зависимости от того, какая скорость ему сообщается, может быть выражена по классической формуле:

(2)

или по релятивистской:

(3)

Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона намного меньше энергии покоя электрона , то может быть применена формула (2); если же сравнима с , то вычисления по формуле (2) приводит к грубой ошибке. В этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3).

1. В формулу энергии фотона подставим значения величин h, c и и, проведя вычисления, для ультрафиолетового излучения получим:

.

Это значение энергии фотона намного меньше энергии покоя электрона МэВ:

Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть вычислена по классической формуле (2):

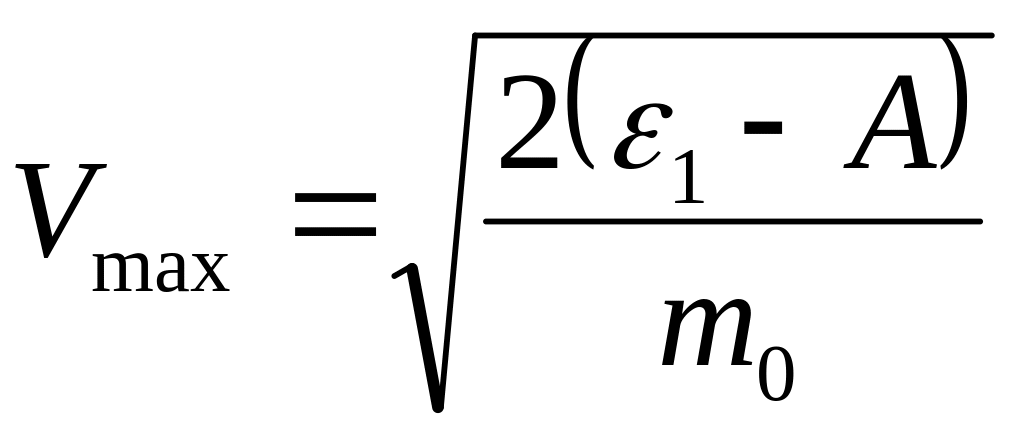откуда . (4)

2. Вычислим теперь энергию фотона γ-излучения:

МэВ

Работа выхода электрона ( эВ) пренебрежимо мала по сравнению с энергией γ-фотона, поэтому можно принять, что максимальная кинетическая энергия равна энергии фотона.

МэВ.

В данном случае кинетическая энергия электрона сравнима с его энергией покоя

.

Следовательно, для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии:

, где .

Выполнив преобразования, найдем:

.

Следовательно, максимальная скорость фотоэлектронов, вырываемых излучением,

М м/с

Ответ: 1) 1,08 М м/с; 2) 226 М м/с.