2. Фотоэлектрический эффект

Фотоэлектрическим эффектом называется испускание электронов веществом под действием света.

• Энергия фотона

,

где - частота света; h – постоянная Планка (6,63 ∙ 10^-34 Дж/с); λ – длина волны; с – скорость света.

• Масса фотона

.

• Импульс фотона

,

где - волновое число; ; – волновой вектор, направленный в сторону распространения волны.

• Уравнение Эйнштейна для внешнего фотоэффекта (формула Эйнштейна):

а) в общем случае

,

где - энергия фотона, падающего на поверхность металла; А – работа выхода электрона из металла;

Т_max – максимальная кинетическая энергия фотоэлектрона;

б) в случае, если энергия фотона намного больше работы выхода ( >>A):

.

Кинетическая энергия фотоэлектрона в зависимости от того, какая скорость ему сообщается, может быть выражена по классической формуле:

(1)

или по релятивистской:

, или (2)

где - ; m – масса релятивистского электрона.

Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона намного меньше энергии покоя электрона Е₀ = m₀c², то может быть применена формула (1), если же сравнима с Е₀, то вычисления по формуле (1) приводят к грубой ошибке. В этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (2).

• Красная граница фотоэффекта:

(при Т_max = 0);

,

где - максимальная длина волны излучения;

- минимальная частота.

• Коротковолновая граница тормозного рентгеновского излучения

,

где U – ускоряющая разность потенциалов.

3. Давление света

• Давление, производимое светом при нормальном падении,

, или

где Е_е – облучённость поверхности – энергия, падающая на единицу поверхности за единицу времени.

- энергия всех фотонов, падающих на единицу поверхности за единицу времени.

4. Эффект Комптона

• Формула Комптона.

Изменение длины волны рентгеновских лучей при рассеянии на свободных электронах определяется формулой:

,

где λ – длина волны падающего рентгеновского излучения;

- длина волны фотона, рассеянного под углом к первоначальному направлению движения, после взаимодействия с электроном; m – масса электрона отдачи.

• Комптоновская длина волны:

,

(при рассеянии фотона на электроне = 2,436 пм).

2. Примеры решения задач

2.1. Тепловые излучения.

Пример 2.1.1.

Исследование спектра излучения Солнца, показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ = 500 нм. Принимая Солнце за чёрное тело, определить: 1) Энергетическую светимость R_T Солнца; 2) Поток энергии, излучаемый Солнцем; 3) Массу m электромагнитных волн, излучаемых Солнцем за 1 с.

Решение:

1) Энергетическая светимость чёрного тела выражается формулой Стефана – Больцмана:

(1)

Температура излучающей поверхности может быть определена из закона смещения Вина: λ_m=b/T. Выразив отсюда температуру и подставив ее в формулу (1), получим

(2)

Произведя вычисления по формуле (2), найдем

= 64 МВт/м²

2) Поток энергии Ф_е излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности:

Ф_е = S или Ф_е = 4πR²_С (3)

где R_C– радиус Солнца.

Подставив в формулу (3) значения и произведя вычисления, получим Ф_е = 3,9 ∙ 10²⁶ Вт.

3) Массу электромагнитных волн (всех длин) излучаемых Солнцем за время t = 1 с, определим, применив закон пропорциональности массы и энергии E = mc². Энергия электромагнитных волн, излучаемых за время t, равна произведению потока энергии Ф (мощности излучения) на время: Е=Фt. Следовательно, Ф_е = mс², откуда m = Ф_е/с². Произведя вычисления по этой формуле, найдем m = 4,3 ∙ 10³ кг.

Пример 2.1.2.

Длина волны λ_m, на которую приходится максимум энергии в спектре излучения черного тела, равна 0,58 мкм. Опре­делить максимальную спектральную плотность энергетической светимости (r _λ,т)_max, рассчитанную на интервал длин волн Δλ= 1 нм, вблизи λ_m.

Решение. Максимальная спектральная плотность энергети­ческой светимости пропорциональна пятой степени температуры Кельвина и выражается формулой

(1)

Температуру Т выразим из закона смещения Вина λ_m = b₁/T, откуда T=b₁/λ_m.

Подставив полученное выражение температуры в формулу (1), найдем (2).

В таблице значение b₂ дано в единицах СИ, в которых единичный интервал длин волн Δλ = 1 м. По условию же задачи требуется вы­числить спектральную плотность энергетической светимости, рас­считанную на интервал длин волн 1 нм, поэтому выпишем значение С в единицах СИ и пересчитаем его на заданный интервал длин волн:

b₂ = 1,30 ∙ 10^-5 Вт/(м³ ∙ К⁵) = 1,30 ∙ 10^-5 Вт/(м²∙м∙К⁵) = 1,30 ∙ 10^-14 Вт/(м²∙нм∙К⁵).

Вычисление по формуле (2) дает

(r_λ,T)_max = 40,6 кВт/(м∙нм).

Пример 2.1.3.

Электрическая печь потребляет мощность Р = 500 Вт. Температура ее внутренней поверхности при открытом небольшом отверстии диаметром d = 0,5 см равна 700⁰ С. Какая часть потребляемой мощности рассеивается стенками?

Решение:

При установившемся тепловом режиме печи вся ежесекундно потребляемая ею электрическая энергия (т.е. мощность) Р излучается наружу отверстием и стенками, следовательно,

, (1)

где Ф_э^’ и Ф_э^’’ – потоки излучения , испускаемые отверстием и стенками соответственно. В задаче требуется найти отношение , (2)

Рассматривая излучение печи через небольшое отверстие в ней как излучение абсолютно черного тела, из формулы и закона Стефана – Больцмана находим

Ф_э^’ = R_эS = σT⁴πd²/4. (3)

По формуле (2) и с учетом (3) получим

.

Подставив в формулу числовые значения величин, выраженных в единицах СИ, и выполнив вычисление, найдем ответ:

Пример 2.1.4.

Какую энергетическую светимость имеет затвердевающий свинец? Отношение энергетических светимостей свинца и абсолютно черного тела для данной температуры (T = 600К)

Решение:

Энергетическая светимость «серого тела» определяется уравнением:

R_T^’ = a_τ ∙ R_э , (1)

где a_τ – поглощательная способность серого тела;

= a_τ – коэффициент поглощения затвердевающего свинца; R_э – энергетическая светимость (излучательность) абсолютно черного тела.

, (2)

где - спектральная плотность энергетической светимости; - постоянная Стефана – Больцмана; T – абсолютная температура излучающего тела;

Подставляя выражение (2) в (1), получим:

R_э^’ = ∙ = 0,6 ∙ 5,67 ∙10^-8 ∙ 600⁴ = 4,6 кВт/м².

Ответ: R_э^’ = 4,6 кВт/м².

Пример 2.1.5

Какую энергетическую светимость R_э имеет абсолютно черное тело, если максимум спектральной плотности его энергетической светимости приходится на длину волны

λ = 484 нм.

Решение:

Энергетическая светимость R_э поверхности абсолютно черного тела определяется по закону Стефана – Больцмана:

,

Из закона смещения Вина , тогда получим:

Вт/м².

Ответ: R_э = 73,5 МВт/м².

Пример 2.1.6.

В спектре Солнца максимум спектральной светимости приходится на длину волны λ₀ = 0,47 мкм. Приняв, что Солнце излучает как абсолютно черное тело, найти интенсивность солнечной радиации (т.е. плотность потока излучения) вблизи Земли за пределами ее атмосферы.

Решение:

Согласно определению плотности потока излучения I, называемой также интенсивностью излучения (радиации), можно записать:

(1)

где W_э – энергия излучения, Ф_э = W_э/t – поток излучения сквозь поверхность S. Сравнивая (1) и видим, что величины I, R_э выражаются в одинаковых единицах.

Очевидно, интенсивность излучения Солнца вблизи Земли пропорционально энергетической светимости поверхности Солнца. Чтобы найти связь между величинами I, R_э, учтем, что весь поток излучения, испускаемый поверхностью Солнца (пусть r - радиус Солнца), проходит сквозь поверхность сферы радиуса r, равного расстоянию от Солнца до Земли: Ф_э = R_э4πr_c² = I4πr², отсюда:

I = R_эr_c²/r² (2)

Используя закон Стефана – Больцмана и вычислив температуру солнечной поверхности по закону смещения Вина, находим

R_э = σT⁴ = σ(b/λ₀)⁴. (3)

Так как величины r, r_c – табличные, то, записав в (2) вместо R_э ее значение из (3), определим искомую величину:

(4)

Подставим в (4) числовые значения величин, выраженные в СИ и выполнив вычисление, получим

I = 1,8 ∙ 10³ Вт/м² = 1,8 кВт/м².

Пример 2.1.7.

Поверхность тела нагрета до температуры К. Затем одна половина этой поверхности нагревается на К, а другая охлаждается на К. Во сколько раз изменится светимость поверхности этого тела?

Дано:

К

К

К

Решение:

Энергетическая светимость поверхности абсолютно черного тела определяется по закону Стефана – Больцмана:

Отсюда .

Ответ: увеличится в 1,06 раз.

Пример 2.1.8.

Н асколько уменьшится масса Солнца за год вследствие излучения? За какое время масса Солнца уменьшиться вдвое? Температура поверхности солнца К. Излучение Солнца считать постоянным.

Дано:

К

м

с

Решение:

Энергия, излучаемая Солнцем за время равна:

тогда .

кг.

лет.

Ответ: кг; лет.

Пример 2.1.9.

Определить температуру поверхности Солнца, если известно, что на границе земной атмосферы плотность потока солнечного излучения равна Излучение Солнца считать близким к излучению абсолютно черного тела.

Решение:

Плотность потока волнового излучения, испускаемого единицей поверхности абсолютной черного тела, определяется законом Стефана – Больцмана:

Отсюда

Для изменения значения плотности потока надо полную мощность W излучения Солнца разделить на площадь его поверхности:

Полную мощность излучения Солнца определим из выражения:

где S – поверхность сферы, имеющей радиус , равный расстоянию от Солнца до Земли.

Так как , то

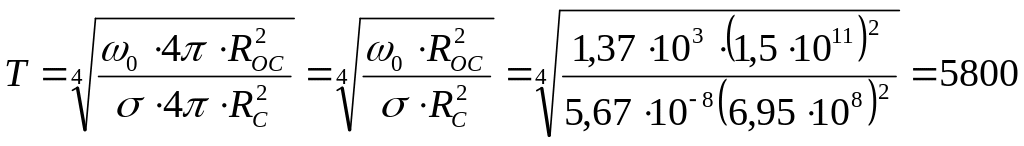К.

Ответ: К.

Пример 2.1.10.

Д лина волны, на которую приходится максимум энергии излучения Солнца, мкм. Найти изменение массы Солнца за время t = 10 лет. Солнце считать абсолютно черным телом.

мкм

лет

Решение:

Изменение массы Солнца за 10 лет определим отношение излученной им энергии к квадрату скорости света c:

(1)

Излученную энергию найдем, умножив

интегральную светимость Солнца на площадь поверхности Солнца и время

или (2)

Согласно закону Стефана – Больцмана:

. (3)

Абсолютную температуру солнца найдем из закона смещения Вина:

(4)

Подставим выражение (4) в (3):

(5)

Теперь подставим выражение (5) в (2):

(6)

Подставим формулу (6) в (1):

или

Ответ: .

Пример 2.1.11.

В спектре Солнца максимум спектральной плотности энергетической светимости приходится на длину волны

λ₀ = 0,47 мкм. Приняв, что Солнце излучает как абсолютно черное тело, найти интенсивность солнечной радиации (т.е. плотность потока излучения) вблизи Земли за пределами ее атмосферы.

Согласно определению плотности потока излучения , называемой так же интенсивностью излучения (радиации), можно записать:

(1)

где W_э – энергия излучения, Ф_э = W_э / t – поток сквозь поверхность S. Сравнивая выражения (1) и энергетическую светимость R_Т = , видим, что величины I,R_Т выражаются в одинаковых единицах.

Очевидно, интенсивность излучения I Солнца вблизи Земли пропорциональна энергетической светимости R_э поверхности Солнца. Чтобы найти связь между величинами I,R_э, учтем, что весь поток излучения, испускаемый поверхностью Солнца (пусть R_С – радиус Солнца), проходит сквозь поверхность сферы радиуса r, равного расстоянию от Солнца до Земли:

отсюда:

. (2)

Используя закон Стефана – Больцмана и вычислив температуру солнечной поверхности по закону смещения Вина λ₀T = b, находим

(3)

Так как величины r, r₀ – табличные, то записав в (2) вместо R_э ее значение из (3), определим искомую величину:

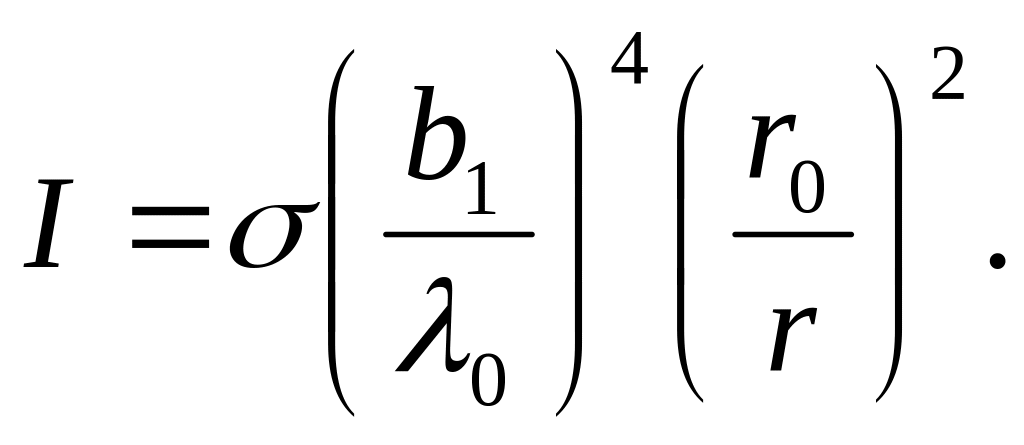(4)

Подставим в формулу (4) числовые значения величин, выраженных в единицах СИ: λ₀ = 0,47 ∙ 10^-6 м, R_C = 6,95 ∙ 10⁸ м, r = 1,50 ∙ 10¹¹ м, σ = 5,67 ∙ 10^-8 Вт/(м² ∙ Т⁴), b = 2,90 ∙ 10^-3 м ∙ К. Выполнив вычисление, получим

1,8∙10³ Вт/м² = 1,8 кВт/м²