ФГБОУ ВПО «Воронежский государственный технический университет»

Кафедра технологии машиностроения

- 2015

Методические указания

и варианты заданий

к выполнению контрольной работы № 1

по дисциплине

«Математическое моделирование

в машиностроении»

для студентов направления

15.03.05 «Конструкторско-технологическое обеспечение

машиностроительных производств»

заочной формы обучения

Воронеж 2015

Составитель канд. техн. наук А.В. Перова

УДК 519.868+621.01

Методические указания и варианты заданий к выполнению контрольной работы № 1 по дисциплине «Математическое моделирование в машиностроении» для студентов направления 15.03.05 «Конструкторско-технологическое обеспечение машиностроительных производств» заочной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. А.В. Перова. Воронеж, 2015. 24 с.

Методические указания включают краткие теоретические сведения по целям и задачам дисциплины «Математическое моделирование в машиностроении», варианты, методику и порядок выполнения контрольной работы, снабжены перечнем рекомендуемой литературы и конкретными примерами моделирования с использованием статистических моделей.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word XP и содержатся в файле Контрольная работа№1_МММ.doc.

Табл. 6. Ил. 2. Библиогр.: 7 назв.

Рецензент д-р техн. наук, профессор Е.В. Смоленцев

Ответственный за выпуск зав. кафедрой, профессор

И.Т. Коптев

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© ФГБОУ ВПО

«Воронежский государственный

технический университет», 2015

1. Цель и задачи дисциплины

Цель преподавания дисциплины - приобретение навыков разработки и использования математических моделей для описания, исследования и оптимизации процессов в машиностроении.

Задачи изучения дисциплины:

- ознакомление с общими понятиями математического моделирования процессов в машиностроении (структуры, классификации и областей применения математических моделей, предъявляемых к ним требований );

- освоение теоретических основ математического моделирования и оптимизации процессов в машиностроении;

- изучение вопросов математического моделирования физических процессов в технологических системах;

- освоение вопросов математического моделирования и оптимизации технологических станочных систем.

 

2. Общие понятия математического моделирования процессов в машиностроении

 Под объектами моделирования в машиностроительном производстве следует понимать:

1. Технологические системы (ТС) – участки из универсальных станков, автоматические линии, гибкие производственные системы (ГПС).

2. Технологические процессы (ТП).

3. Физические процессы (ФП) – процессы, протекающие при резании металлов, при функционировании технологического оборудования в упругой системе СПИД и т.д.

В данном курсе рассматриваются математические модели технологических систем и физических процессов.

В чистом виде (по – отдельности) математические модели данных объектов применяются редко, как правило, они комбинированные. Например, в математических моделях ТС используются математические модели ТП, в которых, в свою очередь, применяются математические модели ФП.

Математическая модель объекта моделирования – это система математических элементов (чисел, переменных, уравнений, неравенств, множеств, матриц, графов и т.д.) и отношений между ними, адекватно отражающая некоторые свойства объекта, существенные с точки зрения инженера, для решения той или иной задачи.

Математические модели разрабатываются для:

1. Описания ФП, ТП, ТС.

2. Исследования ФП, ТП, ТС.

3. Проектирования ТП, ТС.

Оптимизации в ходе проектирования ТП, ТС и организации работы ТС.

Построения систем автоматизированного проектирования.

Вид, состав, сложность математической модели зависит от того, какой объект она описывает и для каких целей разработана.

3. Общие указания по выполнению контрольной работы

Объём и содержание контрольной работы соответствуют рабочей программе курса "Математическое моделирование в машиностроении". Контрольная работа содержит два задания. Номера вариантов заданий выбираются согласно двум последним цифрам шифра студенческого билета из таблицы 1.

4. Задание 1

Математическое моделирование поверхностного пластического деформирования поверхностей

тороидальным роликом

При поверхностном пластическом деформировании деталей, для получения требуемой шероховатости, необходимо обеспечить определенное давление в зоне контакта, которое известным образом [1] зависит от площади пятна контакта.

Цель задания — определить размеры ролика и угол его наклона для обеспечения требуемой площади пятна контакта при заданном натяге.

Таблица 1

Предпоследняя цифра Х соответствует номеру 1, 3, 5, 7, 9	Предпоследняя цифра Х соответствует номеру 0, 2, 4, 6, 8
Х0 – вариант 1	Х0 – вариант 11
Х1 – вариант 2	Х1 – вариант 12
Х2 – вариант 3	Х2 – вариант 13
Х3 – вариант 4	Х3 – вариант 14
Х4 – вариант 5	Х4 – вариант 15
Х5 – вариант 6	Х5 – вариант 16
Х6 – вариант 7	Х6 – вариант 17
Х7 – вариант 8	Х7 – вариант 18
Х8 – вариант 9	Х8 – вариант 19
Х9 – вариант 10	Х9 – вариант 20

Теоретические основы

При составлении расчетной схемы (рис. 1) принимаем, что ролик выполнен тороидальным из абсолютно жесткого материала. Обрабатываемая деталь абсолютно плоская и в момент контакта имеет абсолютную податливость. Площадь контакта рассчитываем в проекции на плоскость, параллельную обрабатываемой поверхности.

Для определения координат профиля пятна контакта при принятых упрощениях расчетные формулы имеют вид:

; (1.1)

; (1.2)

; (1.3)

; (1.4)

; (1.5)

; (1.6)

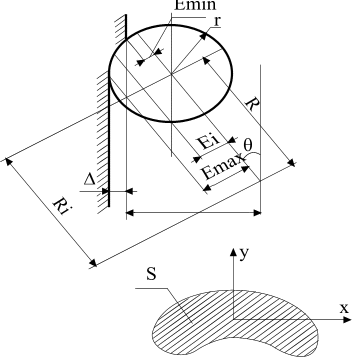
Рис. 1. Расчетная схема процесса поверхностного

пластического деформирования поверхности детали

, (1.7)

где , - параметры, характеризующие расстояние от оси симметрии тора до его крайних сечений, контактирующих с плоскостью, мм;

- радиус тора;

- натяг, мм;

 - угол наклона торового ролика к плоскости обработки, град;

n - число шагов интегрирования (не более 30);

- радиус от центра вращения до оси тора, мм;

 - пересчетный параметр, определяющий угловое расстояние от оси у до места контакта торового круга в сечении с плоскостью обработки, град.;

R_i - значение радиуса окружности при пересечении тора плоскостью на расстоянии E_i от оси симметрии, мм.

Площадь пятна контакта описывается системой параметрических уравнений (1.6 – 1.7), в которых параметром является расстояние от оси симметрии тора до секущей плоскости.

Методика расчета

Для заданного значения натяга необходимо определить угол наклона ролика, обеспечивающего заданное значение площади пятна контакта .

Для вычисления площади пятна контакта, описываемой уравнениями (1.6) и (1.7), используется метод трапеций. Площадь пятна контакта определяется по формуле:

, (1.8)

где , - определяются по уравнениям (1.6), (1.7);

n - число шагов интегрирования или число участков, на которые разбивается площадь пятна контакта.

Изменяя значение угла контакта ролика от 90° до заданного с шагом 1° - 5°, вычисляем площадь пятна контакта по формулам (1.1 - 1.8) для каждого угла от 90° до . В результате получим зависимость площади от угла . Эту зависимость можно проиллюстрировать графически (рис. 2).

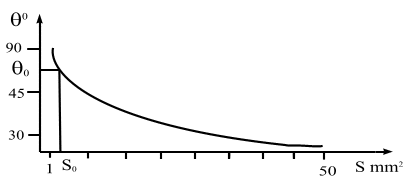
Рис. 2. График зависимости от

По графику определяется угол , обеспечивающий заданную площадь пятна контакта .

Порядок выполнения задания 1

1. Составить алгоритм и программу расчета пятна контакта.

2. Для своего варианта по табл. 2 определить значения , и .

3. Выбрать типоразмер ролика по табл. 2.

4. По вычисленным значениям для различных углов построить график (рис. 2).

5. По графику (рис. 2) определить значения угла , обеспечивавшего заданное значение .

6. Если , то необходимо взять другой типоразмер ролика и повторить расчеты.

Таблица 2

№ варианта		, мм	, мм2
1	60	0,05	2,50
2	50	0,07	3,50
3	45	0,08	4,10
4	55	0,05	2,60
5	70	0,06	2,95
6	55	0,15	7,67
7	40	0,03	1,65
8	65	0,06	3,00
9	45	0,14	7,30
10	50	0,10	5,25
11	40	0,10	5,00
12	45	0,03	1,55
13	50	0,01	0,5
14	60	0,05	2,1
15	50	0,02	1,6
16	45	0,07	3,9
17	55	0,16	7,2
18	40	0,2	1,6
19	70	0,05	3,1
20	65	0,07	3,3

Содержание отчета

1. Алгоритм и программа расчета.

2. Номер варианта задания и исходные значения параметров.

3. Вариант типоразмера ролика.

4. Вычисленные значения и при выбранном числе .

5. График зависимости от .

6. Найденное значение параметра .

Таблица 3

Параметры, мм	Тип ролика
	1	2	3	4	5	6
R	25	30	20	34	25	33
r	4	5	3	6	5	4