2. Амплитудная модуляция аналоговых сигналов

При ам­плитудной модуляции в соответствии с законом передаваемого со­общения меняется амплитуда модулируемого сигнала. А мплитудная модуляция - наиболее распространенный тип аналоговой модуляции в системах радиосвязи, радиовещания и телевидения.

Простейшая разновидность амплитудной модуляции -однотональная (от слова тон - звук одной частоты), при которой модулирующий сигнал представляет собой гармоническое колебание:

(39)

где - амплитуда модулирующего сигнала (максимальная высота синусоиды) ;

- круговая (угловая) частота, ;

- период модулирующего колебания;

- начальная фаза.

В качестве несущего колебания в системах связи и вещания практически всегда применяется высокочастотный гармонический сигнал.

Примем в качестве тестового аналогового сообщения синусои­дальный сигнал:

(40)

Несущие, т.е. модулируемые колебания

(41)

где частота несущих колебаний - частоты модулирующего колебания.

В результате воздействия колебания (40) на амплитуду несущих колебаний (41) получим сигнал с амплитудной модуляцией:

(42)

где - коэффициент амплитудной модуляции.

Графики трех названных колебаний приведены на рис. 13 и рис. 14.

Рис. 13.

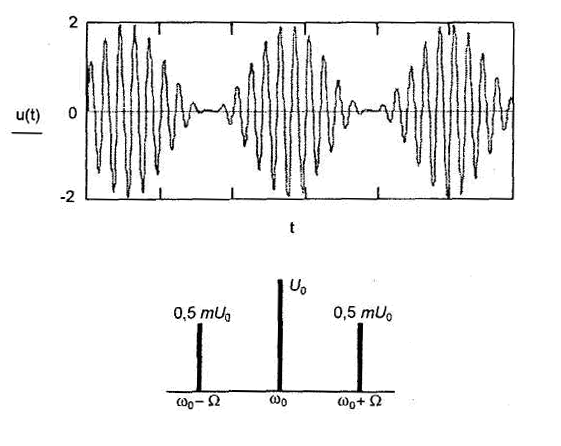
Рис. 14

С целью наглядности на рис. 15, а, б изображены графики модулирующего колебания при , несущего – при .

1. Спектр амплитудно-модулированного сигнала

Из (42) получим выражение:

(43)

которое в соответствии с формулой для произведения тригономет­рических функций приведем к виду

(44)

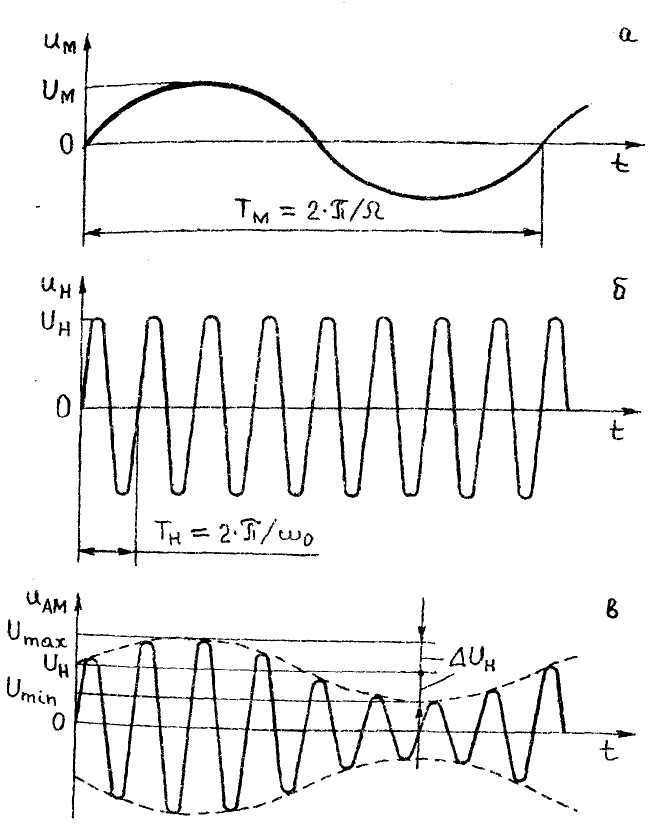из которого следует, что спектр колебания при амплитудной моду­ляции тональным сигналом состоит из трех составляющих с часто­тами: (совпадает с частотой несущей), ( ) (нижняя боковая), ( ) (верхняя боковая). А мплитуда боковой состав­ляющей .

Рис. 15. Амплитудная модуляция

a - модулирующий (управляющий) сигнал; б - несущее колебание (радиочастотный сигнал); в - амплитудно-модулированный сигнал.

Ширина спектра AM колебания . Следовательно, имея базу B=1, сигнал при ампли­тудной модуляции относится к классу узкополосных.

При модуляции более сложным сообщением, занимающим спектр от до (рис. 16,а), соответственно изменится и спектр AM колебания, представленный на рис. 16,б.

Рис. 16

Спектр амплитудно-модулированного сигнала - совокупность простых (гармонических) колебаний (составляющих) разных частот и амплитуд, на которые может быть разложен по частотной оси сложный колебательный процесс, т.е. АМ-сигнал. Аналитическое выражение для такого сигнала с учетом тригонометрической формулы произведения косинусов можно представить в виде суммы колебаний:

(45)

Из формулы (44) видно, что при однотональной модуляции спектр АМ-сигнала состоит из трех высокочастотных составляющих: исходного несущего колебания амплитудой и частотой , а также двух новых гармонических колебаний с разными частотами и , но одинаковыми амплитудами /2, появляющихся в процессе амплитудной модуляции и отражающих передаваемое сообщение.

Колебания с частотами и называют соответственно верхней и нижней боковыми составляющими (частотами). Они расположены симметрично относительно несущей частоты .

Спектр однотонального АМ-сигнала показан на рис. 17. Из рисунка наглядно видно, что ширина спектра АМ-сигнала ( ) при однотональной модуляции равна удвоенному значению частоты модуляции:

(46)

где F – циклическая частота модуляции (модулирующего сигнала).

При отсутствии модуляции (M = 0) амплитуды боковых составляющих равны нулю и спектр АМ-сигнала преобразуется в спектр несущего колебания (составляющая на частоте ). В случае модулирования несущей сигналом сложной формы, состоящим из нескольких гармоник разных частот, каждая гармоника модулирующего (управляющего) сигнала создает две боковые частоты в спектре радиосигнала, расположенные симметрично относительно несущей частоты. Следовательно, спектр такого АМ-сигнала состоит из несущей и двух боковых полос - верхней и нижней. Ширина каждой боковой полосы равна , a ширина спектра сложного АМ-сигнала оказывается равной удвоенному значению наивысшей частоты в спектре модулирующего сигнала (рис. 18).