2.6. Статистическая проверка гипотез

Критерий Пирсона. Для проверки гипотезы о соответствии экс­периментального закона распределения случайной величины теоре­тическому наиболее часто применяют критерий Пирсона или, как его иначе называют, критерий χ² («хи-квадрат»), так как принятие и отклонение гипотезы основаны на χ -распределении.

Предположим, что имеется статистический ряд наблюдений над случайной величиной X. Требуется проверить, согласуются ли экс­периментальные данные с гипотезой о том, что случайная величина имеет предполагаемый закон распределения, заданный интеграль­ной функцией распределения F(x) или плотностью вероятностей f(x), который в дальнейшем будем называть теоретическим зако­ном распределения.

Первоначально статистический ряд разбивают на k интервалов и подсчитывают число значений случайной величины X в каждом интервале. В результате получают экспериментальный ряд частот:

Следует сразу оговорить, что предпосылкой применения крите­рия χ² является достаточная заполненность интервалов частотами. На практике рекомендуется иметь в каждом интервале не менее 5. ..10 наблюдений. Если число наблюдений в отдельных интервалах мало, имеет смысл объединить эти интервалы.

Исходя из предполагаемого теоретического закона распределе­ния вычисляют частоты т_i в тех самых интервалах, на которые разбит статистический ряд. В результате получают теоретический ряд частот в k интервалах m₁ ,m₂, т₃ ,..., m_к.

Для проверки согласованности теоретического и эксперимен­тального распределения подсчитывают меру расхождения:

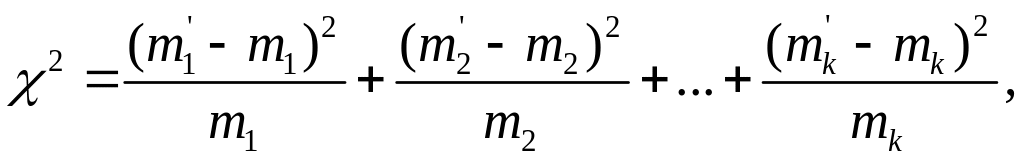
или

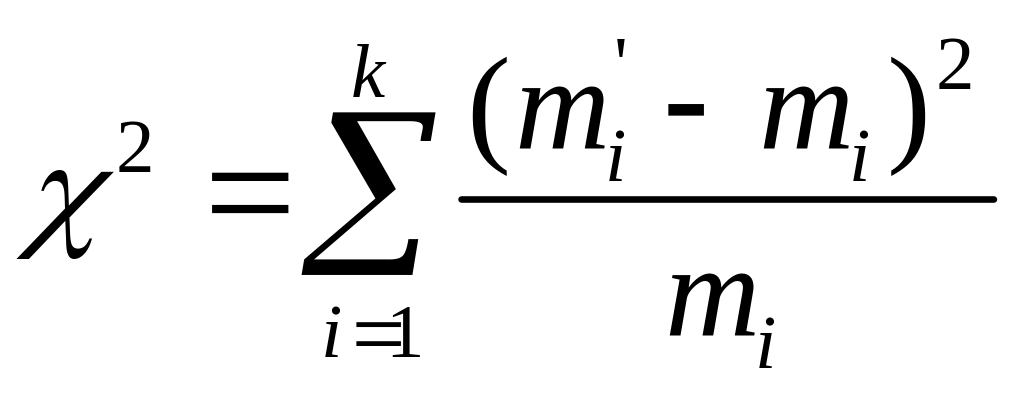(2.41)

и число степеней свободы ν. Число степеней свободы равно в этом случае числу интервалов k минус число ограничений f:

ν = k – f (2.42)

Число ограничений равно числу параметров в рассматриваемом законе распределения, увеличенному на единицу. Например, для гауссовского закона имеется два параметра: [М(х) и σ ] в этом случае число ограничений равно трем.

Для распределения χ² составлены специальные таблицы (см. табл. 2 Приложения [1, с. 399]). Пользуясь этими таблицами, можно для каждого значения χ ² и числа степеней свободы v определить вероят­ность Р того, что за счет чисто случайных причин мера расхождения теоретического и экспериментального распределений (2.41) будет меньше, чем фактически наблюдаемое в данной серии опытов значе­ние χ ². Если эта вероятность Р мала (настолько, что событие с такой вероятностью можно считать практически невозможным), то результат опыта следует считать противоречащим гипотезе о том, что закон распределения величины X есть F(х). Эту гипотезу следует отбросить как неправдоподобную.

Напротив, если вероятность Р сравнительно велика, можно при­знать расхождение между теоретическим и экспериментальным рас­пределениями несущественным и отнести его за счет случайных причин. Гипотезу о том, что величина X распределена по закону F(x), можно считать в этом случае правдоподобной, по крайней мере не противоречащей полученным, экспериментальным данным.

В табл. 2 Приложения [3, с. 399] входами являются значение χ² и число степеней свободы v. Числа, стоящие в таблице, представляют соот­ветствующие значения Р.

Насколько должна быть мала вероятность Р для того, чтобы отбросить или пересмотреть гипотезу,— вопрос неопределенный. Он не может быть решен из математических соображений, а должен базироваться на априорных сведениях о физической сущности из­учаемого процесса.

На практике, если Р<0,1, рекомендуется проверить эксперимент, если возможно — повторить его. В случае появления повторных расхождений следует попытаться найти наиболее подходящий для описания экспериментальных данных закон распределения.

Пример 4. Рассмотрим гипотезу о соответствии закона распределения, представ­ленного статистическим рядом в табл. 2.4, гауссовскому закону распределения. Распределение, полученное по результатам наблюдений, представлено в табл. 2.4 и разбито на 12 интервалов. Первые три и последние два интервала объединим для того, чтобы теоретические частоты получились больше 5. Таким образом, число интервалов станет равным 9. Значения экспериментальных и теоретических частот, подсчитанных исходя из гауссовского закона распределения, приведены в табл. 2.6.

Таблица 2.6

Значения экспериментальных и теоретических частот

	9=1+3+5	16	21	29	31	21	18	9	6=5 + 1
mi	11,6=1,0+3,7-1-6,9	13,4	21,6	28,0	29,3	24,6	168	91	5,6=4,2+1,4

Подставив значения и т_i в выражение (2.41), получим χ ² = 7,52. Число степеней свободы в соответствии с (2.42) равно 6. По табл. 2 Приложения [3, с. 399] находим Р=0,25. Следовательно, распределение значений для напряжения пробоя, приведен­ных в табл. 2.4, близко к гауссовскому.

Критерий Фишера (F-критерий). Для гауссовского закона распределения случайной величины при проверке гипотезы о равенстве выборочных дисперсий в качестве критерия значимости использует­ся параметр, который равен отношению двух независимых оценок дисперсий генеральной совокупности и имеющих соответствен­но степени свободы υ₁ и υ₂, т. е.

F = / (2.43)

При этом должно выполняться условие > , в противном случае следует поменять местами выборочные дисперсии.

Найденное экспериментальное значение F сравнивается с теоре­тическим F_T, которое по числу степеней свободы и при заданном значении коэффициента риска находится из таблицы, построенной для F-распределения (см. табл. 3 Приложения), обладающего тем свойством, что случайные значения отношений дисперсий двух не­зависимых выборок будут не менее F_T по сравнению с заданным коэффициентом риска β. Для практических целей достаточно иметь такие таблицы для β = 0,01 и β = 0,05. Например, β = 0,01 (1%) означает, что отклонения, равного или большего наблюдаемого, можно ожидать только один раз на 100 опытов. Такая малая вероятность указывает на высокую степень значимости. Вот почему иногда вместо коэффициента риска эту вероятность называют уров­нем значимости.

В табл. 3 Приложения значение υ₁ определяет значение F по столбцу, а значение υ₂ — по строке. Если F<F_T, то гипотеза о раве­нстве выборочных дисперсий принимается.

Критерий Кохрена. Для проверки гипотезы о равенстве несколь­ких выборочных дисперсий с одинаковым числом наблюдений в вы­борках используют критерий Кохрена. Для этого, располагая экс­периментальными данными, подсчитывают параметр

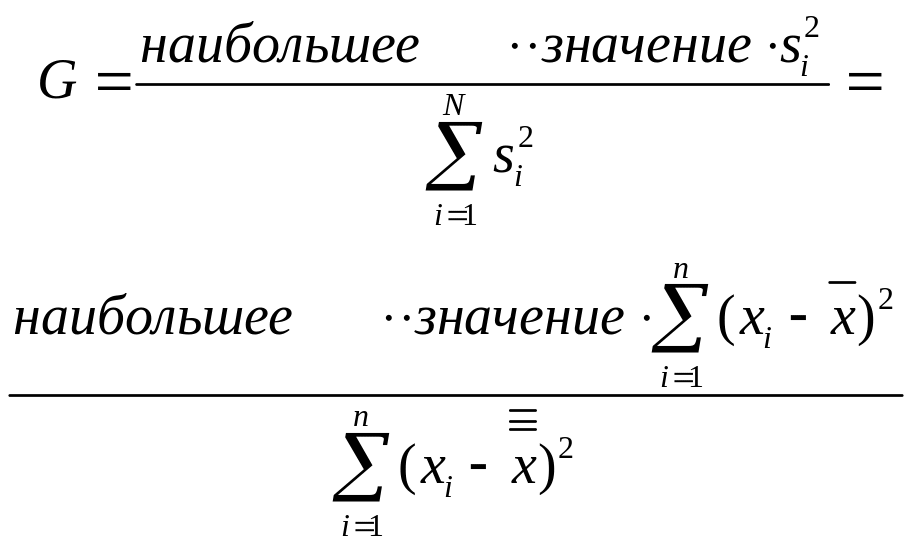(2.44)

где , т. е. вычисляют отношение максимального значения изменчивости среди k выборок к сумме изменчивости всех выборок. Найденное по формуле (2.44) экспериментальное значение G сра­внивают с теоретическим значением G_T. Теоретическое значение находят из таблицы значений критерия Кохрена для гауссовской генеральной совокупности (см. табл. 5 Приложения). Задаваясь коэффициентом риска β (обычно задаются β =0,05 или β = 0,01), по объему выборки п определяют значение G_T по столбцу, а по числу выборок k — значение G_T по строке. Если G<G_T, то результаты не противоречат гипотезе о равенстве выборочных дисперсий.

Критерий Стьюдента (t-критерий). Для проверки гипотезы о равенстве двух выборочных средних значений случайной величины, имеющей гауссовский закон распределения, используется критерий Стьюдента. Для применения данного критерия располагают выбо­рочные средние арифметические значения случайной величины в ра­нжированный ряд от наименьшей величины до наибольшей . Далее подсчитывают величину стандартного отклонения выбороч-1ых средних арифметических значений по формуле

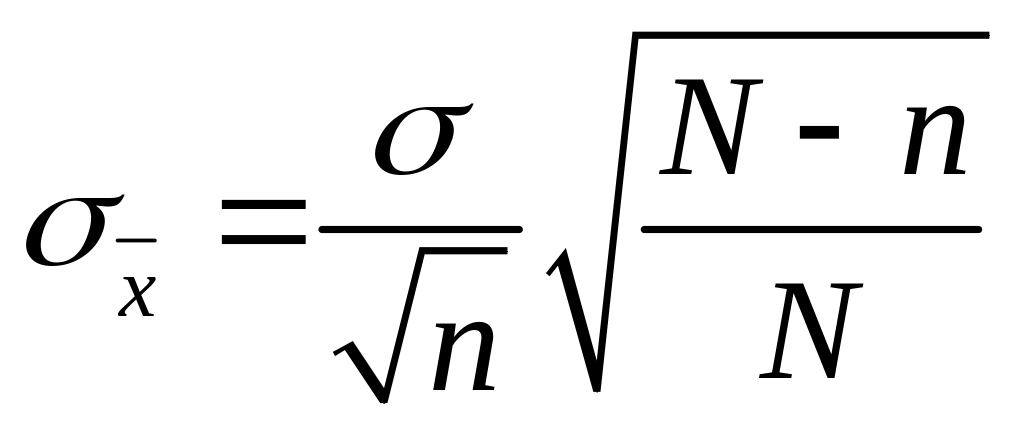(2.45)

Для случая, когда объем выборки п значительно меньше объема партии изделий N, из которой берутся выборки, формула (2.45) имеет вид

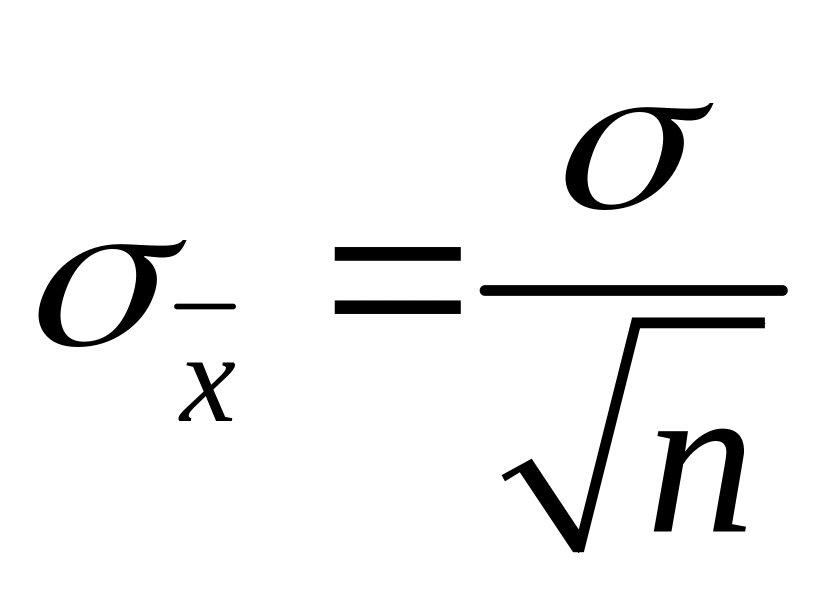(2.46)

Если генеральная характеристика σ неизвестна (а это наиболее часто встречающийся случай), то в формуле (2.46) берется ее оценка

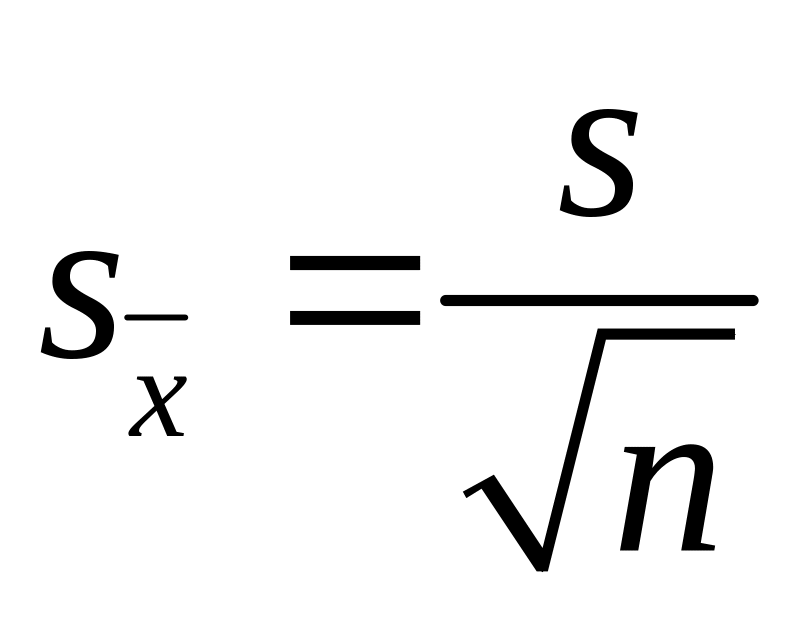(2.47)

После того как определены максимальное и минимальное значения отборочного среднего арифметического и , подсчитывают размах Стьюдента:

(2.48)

Найденное экспериментальное значение t сравнивают с табличными , которое определяют по таблице размаха Стьюдента для экстремальных точек (см. табл. 4 Приложения). При заданном значении коэффициента риска β число степеней свободы υ (в данном случае υ=Nk) определяет значение t_T по строке. Если t<t_т, то гипотеза равенстве выборочных средних арифметических значений принимается, а это значит, что выборки взяты из одной и той же генеральной совокупности.

В заключение следует отметить, что при малом объеме выборки n< 10) t — случайная величина и ее распределение не является .гауссовским. Однако по мере увеличения объема выборки t-распределение приближается к гауссовскому. При n>30 его можно cчитать практическим гауссовским и оно не отличается от распределения α .

К вопросам, связанным со статистической проверкой гипотез о соответствии экспериментального распределения предполагаемому закону распределения случайной величины, близко примыкает вопрос о сглаживании экспериментальных зависимостей.

Пусть проводится опыт, целью которого является исследование зависимости некоторой физической величины У от физической величины X (например, зависи­мость глубины диффузии фосфора в кремниевую пластину от времени диффузии). Предполагается, что величины связаны функциональной зависимостью

у=φ(х). (2.49)

Вид этой зависимости и требуется определить из опыта. Предположим, что в результате опыта мы получили ряд экспериментальных точек и по­строили график зависимости Y от X (рис. 2.7). Обычно экспериментальные точки на таком гра­фике располагаются не совсем правильно — да­ют некоторый разброс, т. е. обнаруживают слу­чайные отклонения от видимой общей законо­мерности. Эти отклонения связаны с неизбеж­ными при всяком опыте ошибками измерения. Тогда возникает типичная для практики задача сглаживания экспериментальной зависимости.

Для решения данной задачи обычно приме­няется расчетный метод, известный под названием метода наименьших квадратов. Этот метод дает возможность при заданном типе зависимости у= φ (х) так выбрать ее числовые параметры, чтобы кривая у= φ(х) наилучшим образом отражала экс­периментальные данные. Вопрос выбора типа кривой у = φ (х) часто решается непо­средственно по внешнему виду экспериментальной зависимости. Например, экс­периментальные точки, изображенные на рис. 2.7, явно наводят на мысль о прямо­линейной зависимости вида у=ах+b.

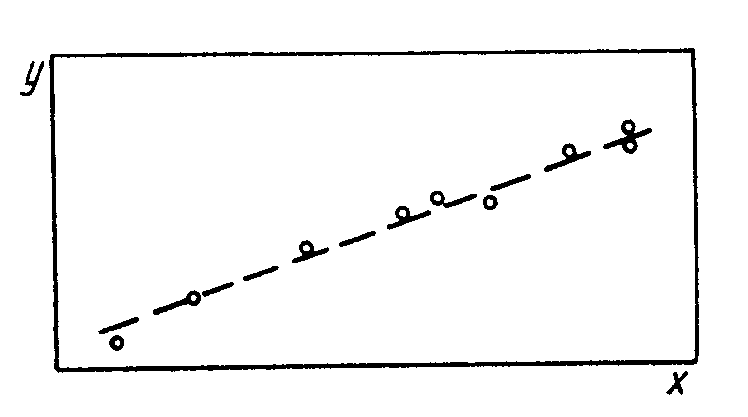
Рис. 2.7. График зависимости y от

Очень часто вид зависимости (линейная, квадратичная, показательная и т. д.) бывает известен из физических соображений, связанных с существом решаемой задачи, а из опыта требуется установить только некоторые параметры этой зависимости.

Вернемся к методу наименьших квадратов. При этом методе требование наилуч­шего согласования кривой у= φ(х) и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум.

Пусть экспериментальная величина У' имеет следующие значения у’₁, у'₂ ,..., у’_i, ..., у_n', а общий вид функции, зависящей от нескольких числовых параметров а, b, с, ..., может быть записан как

у= φ (х; а, b, с, ...) (2.50)

Тогда по методу наименьших квадратов требуется выбрать параметры а, b, с,... так, чтобы выполнялось условие

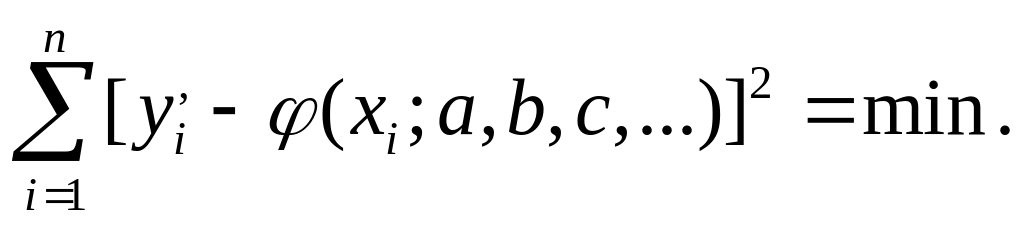(2.51)

Найдем значения а, b, с, ..., обращающие левую часть выражения (2.51) в мини­мум. Для этого продифференцируем ее по этим параметрам и приравняем производ­ные к нулю:

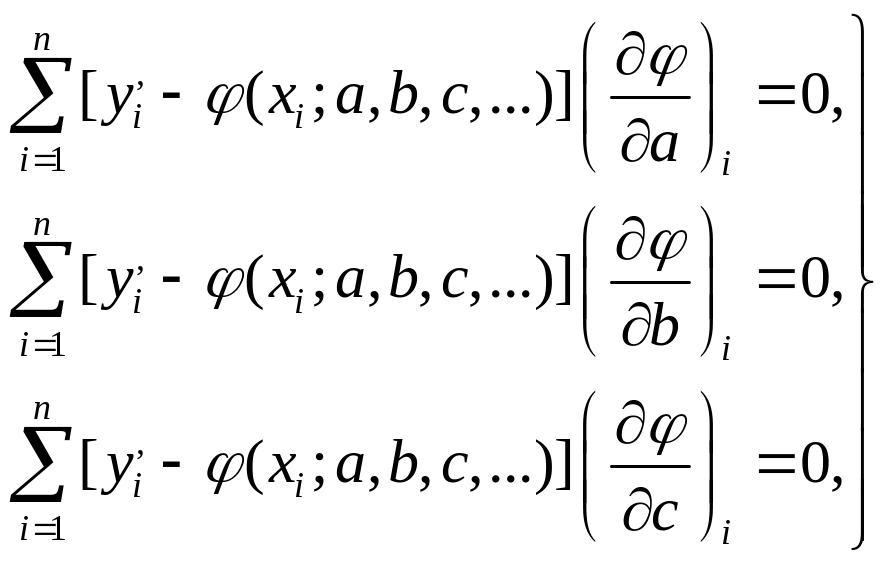(2.52)

где - значение частной производной функции φ по параметру a в точке x_i ; вычисляются аналогично.

Система уравнений (2.52) содержит столько же уравнений, сколько неизвестных а, b, с, ... . Решить систему уравнений (2.52) в общем виде нельзя; для этого необходимо задаться конкретным видом функции φ.