4.3. Оценка генеральной средней м(х) с помощью среднего значения выборки

На практике часто встречаются задачи оценки качества сдава­емой заказчику продукции или технологии ее производства (значе­ние параметров качества которой является генеральной совокуп­ностью) по результатам измеренных параметров качества выборки, взятых из генеральной совокупности. Предположим, что значения параметра качества в генеральной совокупности распределены по закону Гаусса.

При этом могут быть случаи, когда параметры гауссовского распределения генеральной совокупности М(х) и σ известны или когда М(х) известно, а σ неизвестно,

Установление двустороннего критерия для среднего значения , когда σ к М(x) известны. Предположим , что заказчику сдается партия электронных средств объемом N=10000 изделий. В конт­ракте между изготовителем и заказчиком оговорено, что время безотказной работы (параметр качества) сдаваемых ЭС должно быть М(х) = 14600 ч. При этом время отказа изделий из данной партии не должно быть меньше 14000 ч.

Для выяснения вопроса о соответствии этой партии ранее огово­ренным требованиям по параметру качества (время безотказной работы) была взята выборка объемом n =100 изделий, которые были подвергнуты ускоренным испытаниям на отказ [7]. Результаты испытаний приведены в табл. 4.1.

Среднее время наработки на отказ для приведенных в табл. 4.1 изделий составляет = 14,591.

Для определения σ можно воспользоваться формулой (4.1), где следует заменить на х. Тогда ε = ασ, где ε в соответствии с требова­нием заказчика составит 600 ч.

Выбрав по табл. 1 Приложения [3] максимальное α, можно опреде­лить значение σ. Возьмем для простоты расчета α = 3,0 (трехсигмовый предел), в результате σ = 200 ч.

С помощью следует оценить М(х) для данной партии изделий. Воспользуемся (4.1), которое запишем в следующем виде:

Р{ -ε≤ М(х) ≤ + ε }=Ф₁(α),

где Ф₁(α) — вероятность того, что искомое значение М(х) будет лежать в указанных пределах.

Таблица 4.1

Результаты испытаний эс на безотказность работы

Номер образца	Время безотказной работы, тыс. ч
1...5	14,12	14,55	14,26	14,43	14,50
6...10	14,46	14,15	14,40	14,22	14,61
11 ..15	14,24	14,42	14,03	14,35	14,18
16...20	14,48	14,51	14,52	14,62	14,45
21 ..25	14,32	14,14	14,59	14,51	14,54
26...30	14,38	14,27	14,53	14,54	14,64
31. ..35	14,37	14,58	14,56	14,80	14,60
36...40	14,48	14,44	14,50	14,38	14,63
41.. 45	14,45	14,46	14,36	14,52	14,33
46...50	14,65	14,82	14,61	14,49	14,78
51..55	14,81	14,40	14,88	14,47	14,57
56...60	14,94	14,60	14,59	14,64	14,70
61. ..65	14,80	14,62	14,43	14,96	14,53
66...70	14,58	14,85	14,44	14,41	14,79
71. ..75	14,92	14,55	14,84	14,67	14,57
76...80	14,95	14,50	14,06	14,66	14,65
81. ..85	14,71	14,51	14,66	14,94	14,67
86...90	14,14	14,56	14,86	14,69	14,77
91. ..95	14,04	14,71	14,79	14,73	14,68
96...100	14,78	14,93	14,68	14,75	14,70

Задавшись, например, вероятностью Ф₁(α)= 0,99, по табл. 1 Приложения определим значение α = 2,58, после чего не представляет труда определить минимально возмож­ное значение М(х) для данной партии, которое будет равно

Следовательно, предъявленная партия изделий соответствует запи­санным в контракте требованиям по приведенному параметру каче­ства.

При контроле качества технологического процесса производства электронных средств средняя арифметическая характеризует сте­пень отлаженности (настройки) технологического процесса и пото­му является важной характеристикой при его контроле. По значе­нию можно сделать вывод, имеет место нарушение технологичес­кого процесса или нет. Для этого предварительно устанавливают допустимые границы ε изменения значений параметра. В случае известного значения σ, задаваясь α, а следовательно допустимыми границами, можно определить вероятность того, что разность М(х) — будет находиться в пределах этих границ. Искомое значе­ние вероятности Р получается удвоением величины вероятности Ф(α ), найденной но табл. 1 Приложения, [3] т. е. Р = Ф₁(α)=2Ф(α).

Например, мы задались пределами изменения для , равными 0,7 . Тогда по табл. 1 Приложения [3] находим, что вероятность этого события равна 0,52, т. е. 48% изделий в этом случае будут от­бракованы. Если полученная вероятность Р, которая является, по сути дела, процентом выхода годных изделий, не устраивает изго­товителя, то задача может быть решена обратным путем. Задаваясь вероятностью того, что соответствует М(х), по табл. 1 Приложе­ния [3] можно определить величину допустимого изменения значений параметра. При этом, задаваясь большой вероятностью, соответст­венно увеличивают допустимые пределы изменения . Например, для вероятности, равной 0,9, пределы изменения равны 1,65 , т. е. за счет увеличения допустимых пределов изменения будет от­браковано только 10% изделий (подразумевается, что в рассмот­ренных случаях является неизменным).

Если контролируемый параметр подчиняется гауссовскому зако­ну распределения, то технологический процесс не имеет отклонений, если значение лежит в заштрихованной области (рис. 4.1), т. е. с каждого края площади, заключен­ной между осью х и кривой гауссовского распределения, исключает­ся по 5%.

Из табл. 1 Приложения [3] видно, что если взять ε =3 , то процент выхода годных изделий будет бли­зок к 100% (99,73%).

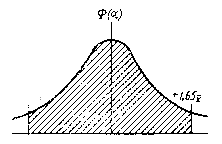
Рис. 4.1 Графическое изображение уравнения Ляпунова

Пример 2. При контроле толщин пластин, распределение которых подчиняется гауссовскому закону, после операции шлифовки допускается отбраковка не более 10% пластин от всей партии. Толщина пластин после шлифовки должна быть M(x)=0,11 мм при среднем квадратическом отклонении σ = 0,01 мм.

Требуется определить величину допустимого отклонения ε при контроле тех­нологического процесса шлифовки пластин.

Решение. Установим объем выборки n = 100, который значительно меньше N. Для подсчета воспользуемся формулой

Так как необходимо, чтобы отбраковывалось не более 10% пластин, то Ф₁(α) = 0,9, т. е. Ф(α)= 0,4505, что соответствует по табл.1 Приложения [3] α = 1,65. Тогда ε =1,65*0,001=0,00165 мм.

Допустимые абсолютные значения для пределов изменения параметра определя­ются с помощью левой части равенства (4.1), которое перепишем в следующем виде:

Р{ М(х)-ε≤ ≤ М(х)+ ε }=Ф₁(α),

Тогда с учетом найденных числовых значений получим

M(x) + 1,65 =0,11+1,65*0,001=0,11165 мм,

M(x) - 1,65 =0,11-1,65*0,001=0,10835 мм.

Следовательно, производственный процесс шлифовки пластин считается удовлетворительным, если среднее значение толщин пластин в выборке лежит в пределах 0,10835 мм ≤ ≤ 0,11165 мм, а нарушение технологического процесса происходит при < 0,10835 мм и > 0,11165 мм.

Такая проверка называется двусторонней, т. е. область отклоне­ния расположена по обеим сторонам от .

Не уменьшая вероятность того, что будет лежать, например, в пределах ±1,65 , можно сузить эти пределы за счет уменьшения .

Действительно, как видно из выражения для , с уменьшением стандартного отклонения генеральной совокупности, из которой берется выборка, т. е. с улучшением качества технологического процесса, уменьшается. Очень часто при практическом примене­нии равенства Ляпунова в формуле для стандартного отклонение средней генеральное среднее квадратическое отклонение σ, кото­рое бывает неизвестным, заменяют средним квадратическим от­клонением s, полученным на основании выборки. Но это не всегда правомерно. Поэтому рассмотрим оценку средней при неизвестном среднем квадратическом отклонении генеральной совокупности.

Установление двустороннего критерия для среднего значения , когда М(х) известно, а σ неизвестно. Рассмотрим случай, когда выборка мала: п≤ 10. Тогда взаимосвязь между допустимыми пре­делами изменения и вероятностью того, что разность между М(х) и окажется в этих пределах, определяется с помощью критерии Стьюдента (или, иначе, t-распределения):

(4.4)

где

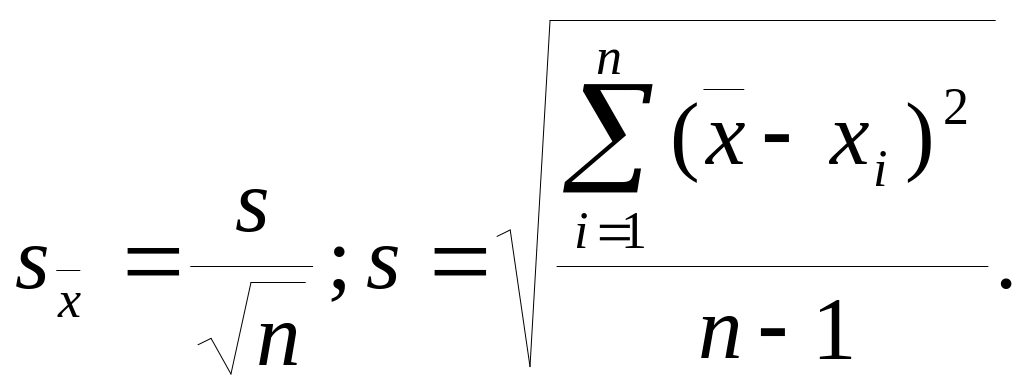
Выражение (4.4) можно переписать в следующем виде:

(4.5)

где

(4.6)

Задаваясь необходимой вероятностью (1—Р), т. е. процентом выхода годных изделий, по таблице для критерия Стьюдента (табл. 4 Приложения) находим искомое значение t_т, зная которое опреде­ляем ε и допустимые пределы изменения .

Пример 3. Возьмем исходные данные на операции шлифовки пластин, аналогич­ные приведенным в примере 1, т. е. М(х)=0,11 мм; должно быть отбраковано не более 10% изделий.

Требуется определить величину ε при условии, что объем выборки n = 9, а тол­щины пластин (мм) в выборке следующие:

х1=0,112, x4=0,116, x7=0,109,

х₂=0,116, х₅=0,118, х₈ = 0,114,

х₃=0,108, х_б=0,111, х₉ = 0,107.

Решение. На основании имеющегося распределения

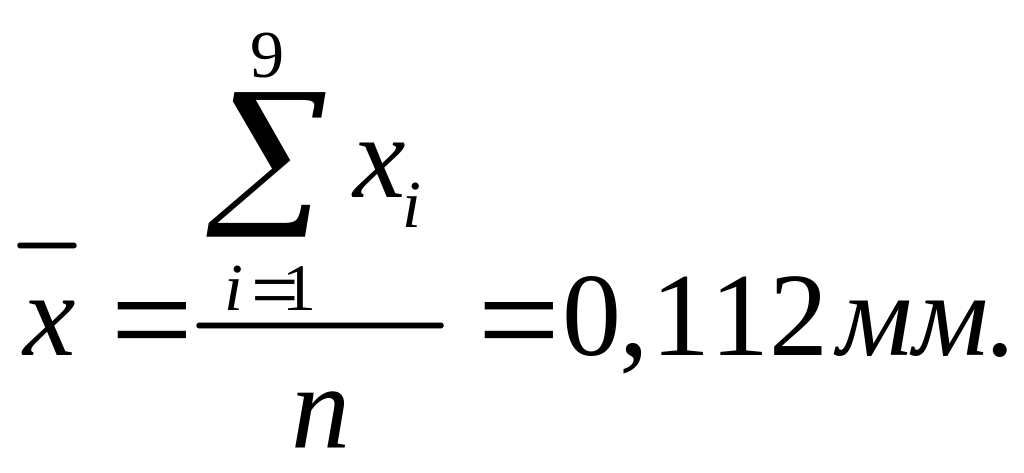
По формуле (2.10) вычислим значение несмещенной оценки среднего квадратического отклонения:

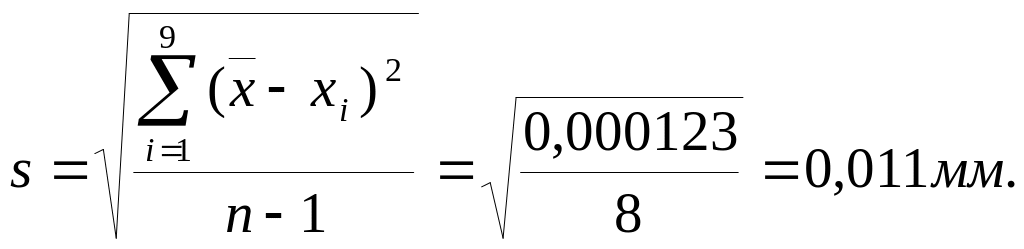
По таблице для критерия Стьюдента находим значение t_т по вероятности (1 - Р) = 1 - 0,9 = 0,1 и числу степеней свободы v = n— 1 =8. Искомое значение t_т равно 1,86. Теперь нетрудно найти по формуле (4.6) значение допустимого отклонения:

Следовательно, допустимыми границами изменения среднего значения толщины пластин будут следующие значения. 0,103 мм ≤ ≤ 0,117 мм.

Если изготовителя такие разбросы толщины пластин не устраивают, то задача решается в обратном направлении. Задается допустимый разброс толщин пластин ε. По формуле (4.6) вычисляется t_т и по табл. 4 Приложения определяется вероятность Р, которая дает процент отбраковываемых пластин.

По мере увеличения объема выборки разница между t-распределением и гауссовским распределением существенно уменьшается. Если n≥100 шт., то применение гауссовской кривой дает почти точные результаты и в этом случае можно пользоваться уравнением (2.49), т. е. t-распределение (или оценка технологического процесса по параметру t) применяется только при небольших выборках.

На практике часто бывает необходимо определить величину генеральной средней по известному значению выборочной средней.

Определение неизвестной генеральной средней по выборочной сре­дней. Пусть имеется генеральная совокупность с гауссовским рас­пределением, причем М(х) и σ неизвестны. Требуется с заданной точностью ε определить вероятность того, что найденная будет равна М(х).

Когда такая задача решена, то обычно говорят, что, полагая приближенно М(х)≈ , мы нашли М(х) с точностью ε и вероят­ностью (1— Р).

Рассмотрим вначале случай малых выборок (n≤10). Тогда, со­гласно распределению Стьюдента,

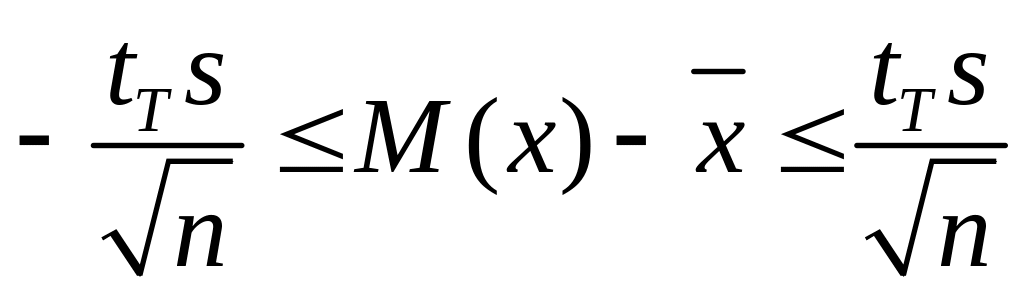
или

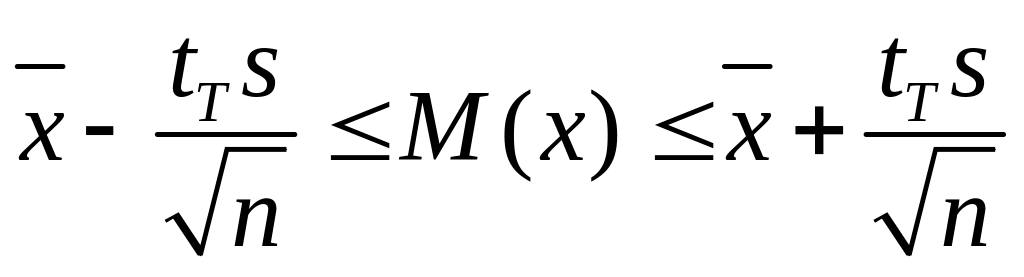(4.7)

Задаваясь значением ε, можно вычислить t_т, а затем по таблице для критерия Стьюдента найти (при известной величине v = n— 1) вероятность Р того, что величина М(х) не будет лежать в пределах (4.7), или вероятность (1— Р) того, что неравенство (4.7) будет выполняться. При этом значения и s при фиксированной выборке п нетрудно вычислить.

Вопрос может решаться и иначе. Можно, задаваясь вероятно­стью (1 —Р), определить границы, в которых будет находиться неизвестное М(х). В этом случае по заданному значению Р и числу степеней свободы v = n— 1 ищем в таблице распределения Стьюдента значение t_т. Зная t_т, нетрудно вычислить точность ε и при извест­ном найти границы для М(х), которые обычно определяются при вероятности (1 — Р), равной или большей 0,95.

Если число изделий в выборке n≥20, то пользуются таблицей для гауссовского распределения. Задаваясь вероятностью Ф₁(α), по этой таблице находят α по величине Ф(α) = Ф₁(α)/2, а затем уже точность .

Сравнение однородных средних. Предположим, что на двух тех­нологических линиях выпускается однотипное изделие. Возьмем выборку n₁ с одной линии, а выборку n₂ — с другой. Предположим далее, что первый ряд наблюдений дал среднюю арифметическую и второй — . Если окажется (а это чаще всего бывает), что эти две средние будут отличны одна от другой, то возникает вопрос, можно считать эту разность случайной и несущественной или нет.

Опять рассмотрим случай малых выборок. Тогда величина

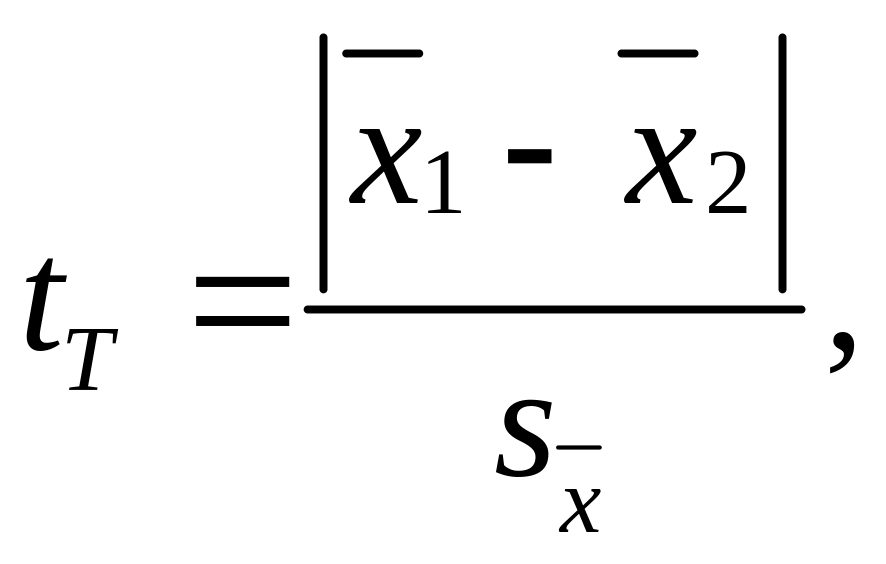(4.8)

где

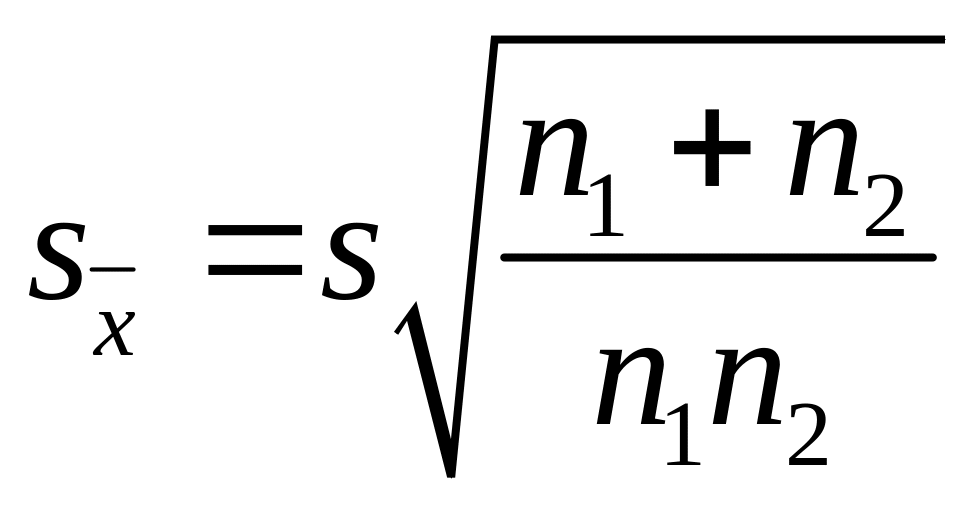(4.9)

при

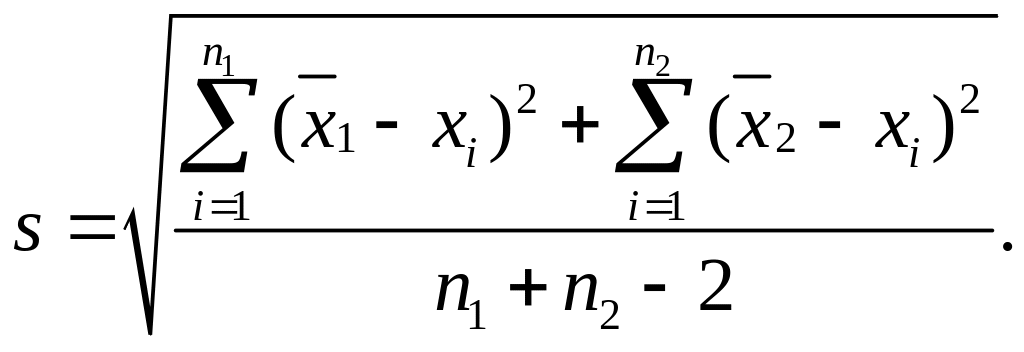(4.10)

По найденному значению t_т и числу степеней свободы v=n₁ + n₂ — 2 находим в таблице критерия Стьюдента (см. табл. 4 Приложения) вероятность появления случайного события. Если полученная вероятность Р≤0,05, то это расхождение является не­случайным и нужно искать его причину. Этот же метод можно использовать при сравнении эффективности изменения той или иной технологической операции.

Предположим, что введены какие-то усовершенствования в тех­нологию с целью изменения определенного показателя качества. Если показатель качества подчиняется гауссовскому закону рас­пределения, то сравнение (средней выборки при первоначальной технологии) и (средней выборки при измененной технологии) с помощью критерия Стьюдента дает объективный ответ на вопрос, является происшедшее улучшение показателя качества после введе­ния усовершенствования в технологию случайным явлением или обусловлено изменением технологического процесса.

Аналогично можно сравнивать результаты изменений на двух однотипных установках, решать вопрос о том, взяты две выборки или более из одной генеральной совокупности или нет и т. д.

Для больших выборок (п > 20...30) можно пользоваться гауссовским распределением. В этом случае

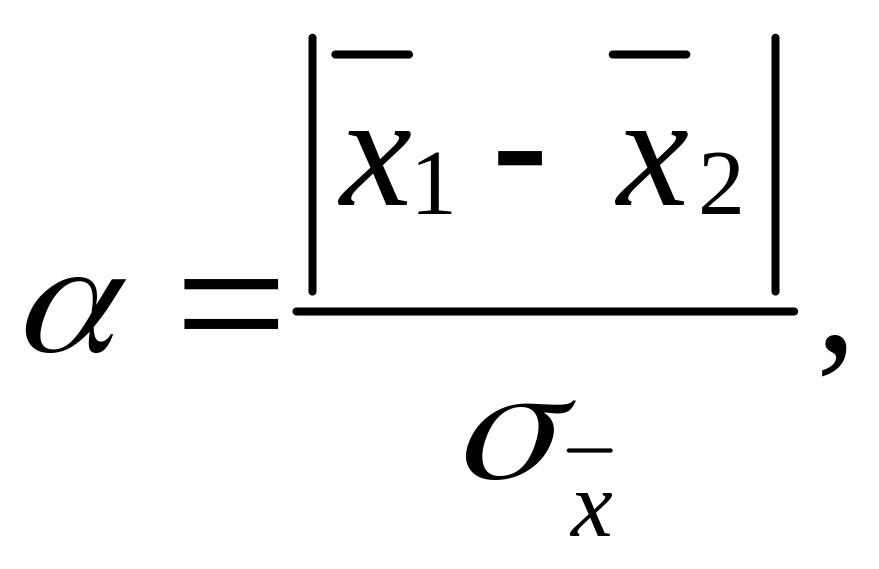(4.11)

где

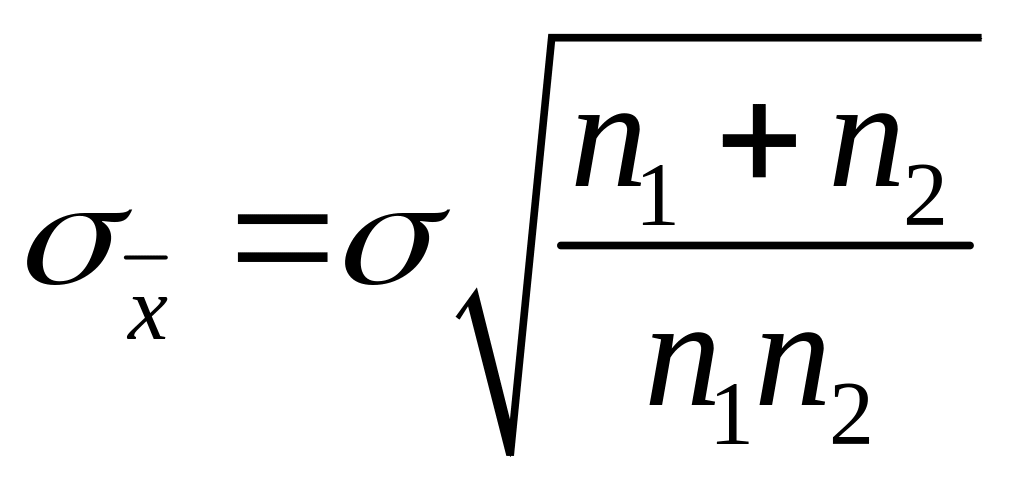(4.12)

при

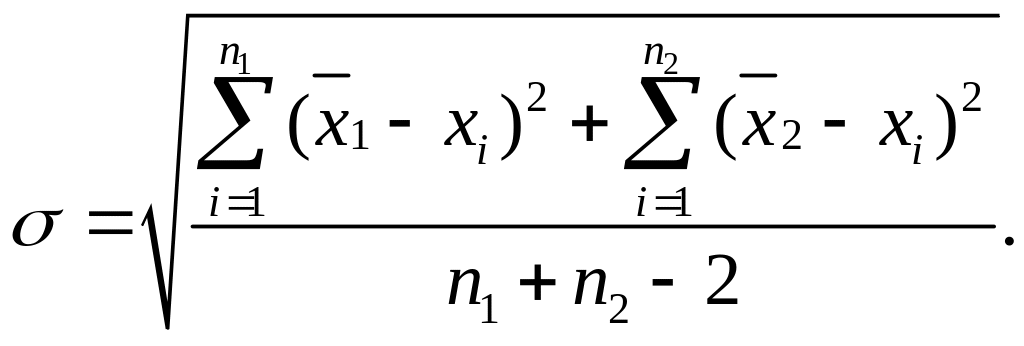(4.13)

Определяя α по табл. 1 Приложения, находим Ф(α). Если Ф₁(α) = 2Ф(α) ≥0,95, то расхождение нужно считать неслучайным.