2.3. Численные методы представления статистического ряда

Графические методы представления однородной совокупности, давая более наглядную картину характера распределения параметра качества, чем таблицы, в то же время не могут быть применены для достоверной оценки качества продукции по результатам контроль­ной выборки. В этом случае удобно представить статистический материал не графически, а числовыми значениями, которые до некоторой степени отражают существенные характеристики стати­стического ряда — характеристики положения и рассеивания слу­чайной величины.

Важнейшей характеристикой положения случайной величины яв­ляется средняя арифметическая величина наблюдаемых значений параметра качества (или просто средняя), которую для характери­стики выборки будем называть, выборочной средней арифметичес­кой и обозначать через . Если в результате п измерений получены значения x₁,x₂, ..., х_n, то

(2.3)

Пример 1. Если из табл. 2.2а взять пять первых значений пробивного напряжения, т.е. 179,180,181,182, 183, то в этом примере n=5 и . Для данной выборки средняя арифметическая

В случае статистического ряда (когда значению параметра соответствует какая-либо частота) средняя арифметическая величина вычисляется по формуле:

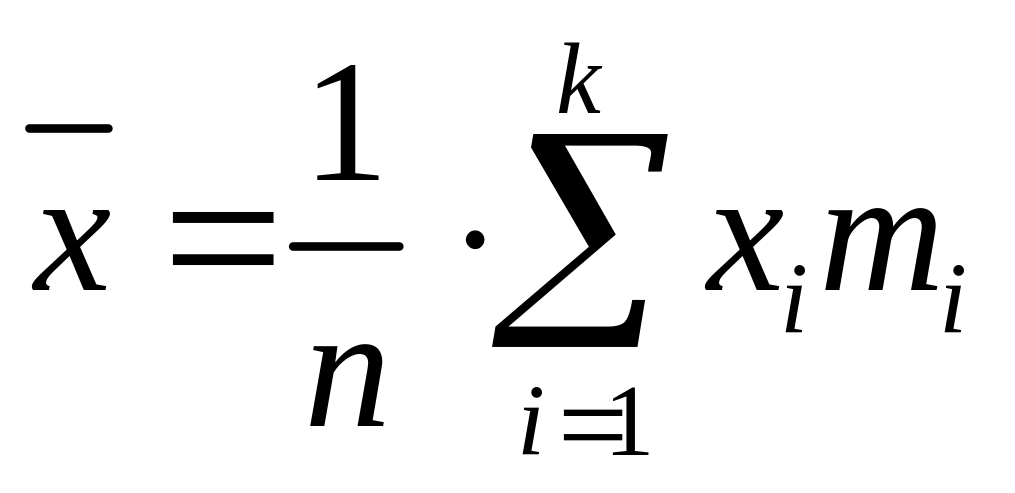(2.4)

где

В этом случае среднюю называют средней взвешенной.

Пример 2. Для упорядоченного ряда, приведенного в табл. 2.2а, число интервалов k=32:

Аналогично вычисляется средняя арифметическая интервального ряда табл. 2.4 с той только разницей, что в качестве значения параметра следует принимать середины интервалов:

Вследствие различной ширины интервалов рассматриваемых рядов обе средние частично не совпадают.

Следует подчеркнуть, что средняя только в том случае является обобщающей характеристикой, когда она применяется к однород­ной совокупности статистического материала,

Кроме важнейшей характеристики положения — средней — при анализе и контроле качества приходится встречаться и с другими характеристиками положения, в частности медианой и модой случай­ной величины.

Если полученные при измерениях значения расположить в воз­растающем или убывающем порядке, то медианой будет значение Me, занимающее серединное значение в ряду. Таким образом, меди­ана — это значение параметра, которое делит упорядоченный ряд на две равные по объему группы. При нечетном числе измерений, т. е. при n =2i+1, значение параметра для случая i+1 будет медиан­ным. При четном числе измерений (2i) медианой является средняя арифметическая двух значений, расположенных в середине ряда.

Таким образом, формулы для вычисления медианы имеют сле­дующий вид:

(2.5)

для случая нечетного числа измерений;

(2.6)

для случая четного числа измерений.

Пример 3. Возьмём из табл. 2.3 пять первых значений пробивного напряжения (х₁=179, х₂=180, х₃=181, х₄=182, х₅=183),т.е. нечётное число измерений, расположенных в возрастающем порядке. Находим медиану: (2i+1)=5, откуда 2i=4, i=2. По формуле (2.5) получим

Если из табл. 2.2а взять только четыре первых значения пробивного напряжения (х₁=179,х₂=180,х₃=181,х₄=182), т. e. четное число измерений, то 2i=4, i=2. По формуле (2.6),

Значение медианы легко определяется графически с помощью кумулятивной кривой (см. рис. 2.3). Так как по оси ординат отложены накопленные частоты, то, разделив отрезок ординаты, соответствующий 100% наблюдений, пополам и восстановив из его середины перпендикуляр, мы получим медиану геометрически как абсциссу точки пересечения перпендикуляра с кумулятивной кривой.

Модой случайной величины называется значение параметра, которое наиболее часто встречается в данном ряду. Условимся обозначать моду через Мо. Для дискретного ряда мода определяется по частотам наблюдаемых значений параметра качества и соответствуют значению параметра с наибольшей частотой.

В случае непрерывного распределения с равными интервалами модальный (т.е. содержащий моду) интервал определяется по наибольшей частоте; в случае неравных интервалов - по наибольшей плотности. Плотность вычисляется как отношение частоты к продолжительности интервала.

Средние величины, характеризуя однородную совокупность одним числом, не учитывают рассеивание наблюдаемых значений параметра качества. Для отображения рассеивания в математической статистике применяют ряд характеристик. Самый простой из них является размах R. Размах представляет собой величину неустойчивую, зависящую от случайных обстоятельств и поэтому применяемую, как правило, в качестве приблизительной оценке рассеивания. Однако, как будет показано ниже, размах бывает очень удобно применять в контрольных картах. Размах R сравнительно легко вычисляется как разность между наибольшим и наименьшем значениями ряда наблюдений:

R = x_max - x_min (2.7)

Другая статистическая характеристика рассеивания наблюдаемых значений показывает, как тесно группируются отдельные значения вокруг средней арифметической или как они рассеиваются вокруг этой средней. Так как алгебраическая сумма отклонения отдельных значений x_i от средней арифметической x равна нулю и непригодна в качестве меры рассеивания, за меру рассеивания принимают сумму квадратов отклонений отдельных значений от средней арифметической, делённую на число наблюдений, уменьшенное на единицу. Эту меру называют выборочной дисперсией и обозначают через s².

Для простой статистической совокупности

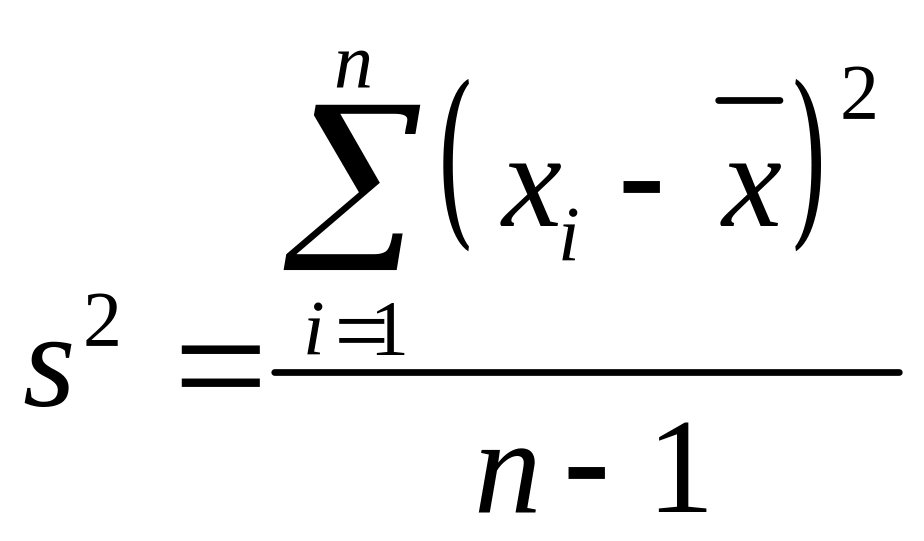(2.8)

При наличии частот m_i

(2.9)

где .

Вместо выборочной дисперсии s² часто применяют выборочное стандартное отклонение s. Оно имеет ту же размерность, что и средняя арифметическая . Выборочное стандартное отклонение для простой статистической совокупности и при наличии частот определяется соответственно по следующим формулам:

(2.10)

(2.11)

Отношение стандартного отклонения к средней арифметической, выраженное в процентах, называют коэффициентом вариации V:

(2.12)

Коэффициент вариации, который также используется как статистическая характеристика рассеивания, показывает относительное колебание отдельных значений около средней арифметической. Коэффициент вариации, являясь безразмерным, удобен для сравнения рассеивания случайной величины с её средним значением.