
- •Математико-статистические методы обработки данных при управлении качеством электронных средств
- •Математико-статистические методы обработки данных при управлении качеством электронных средств Утверждено редакционно-издательским советом
- •Введение
- •1. Общие сведения о контроле качества электронных средств
- •2.2. Графические методы представления статистического ряда
- •2.3. Численные методы представления статистического ряда
- •2.4. Основные понятия теории вероятностей и характеристики генеральной совокупности
- •2.5. Основные законы распределения случайной величины
- •2.6. Статистическая проверка гипотез
- •2.7. Элементы дисперсионного и корреляционного анализа
- •Отклонения толщины фоторезиста от среднего значения при различных частотах вращения центрифуги
- •3. Статистические методы анализа качества. Расслаивание и графические методы
- •3.1. Методы расслаивания
- •3.2. Расслаивание общей изменчивости статистических данных с помощью дисперсионного анализа
- •3.3. Диаграмма разброса (поле корреляции)
- •3.4. Диаграмма Парето
- •3.5. Причинно-следственная диаграмма
- •4. Статистические методы оценки качества
- •4.1. Выбор оценок генеральных характеристик
- •4.2. Определение доверительных интервалов оценок генеральных характеристик
- •4.3. Оценка генеральной средней м(х) с помощью среднего значения выборки
- •Результаты испытаний эс на безотказность работы
- •4.4. Оценка генеральной характеристики рассеивания σ с помощью выборочных характеристик рассеивания
- •4.5. Определение объема выборки для оценки генеральных характеристик с заданной точностью
- •Библиографический список
3.3. Диаграмма разброса (поле корреляции)
Диаграмма разброса применяется для исследования зависимости (корреляции) между двумя видами данных. Поэтому диаграмму разброса часто называют полем корреляции. Диаграмма разброса используется также для выявления причинно-следственных связей показателей качества и влияющих факторов при анализе причинно-следственной диаграммы.
Так, например, с помощью диаграммы разброса очень удобно наблюдать характер изменения параметров качества во времени при воздействии тех или иных факторов. В этом случае по оси абсцисс откладывают начальные значения изучаемого параметра качества, например обратный ток p-n-перехода однотипных полупроводниковых структур (Iобр) перед постановкой эксперимента по изучению влияния определенных факторов (например, температуры, влажности) на данный параметр качества. В результате будем иметь упорядоченный ряд значений x1 ,x2 , х3 , ..., хп параметра качества полупроводниковых структур в момент времени t=0, которые наносят на ось абсцисс. Замерив значения параметра качества у тех же самых полупроводниковых структур по окончании эксперимента, получим ряд значений параметра качества через время t=ti ,представленных в виде упорядоченного ряда y1 ,у2 ,…, уп ,который наносят соответственно на ось ординат. Тогда значение параметра качества каждого изделия до и после эксперимента будет обозначаться точкой в системе указанных координат. Следовательно, все п изделий, подвергшихся эксперименту, будут изображаться разбросанными по координатному полю точками. Эта совокупность точек образует диаграмму разброса (поле корреляции) (рис. 3.2). Если разброс значений изучаемого параметра качества составляет несколько порядков, то удобно применять логарифмический масштаб по обеим осям. Если на одну и ту же точку графика попадает несколько значений параметра, то они обозначаются как точка в круге или в нескольких кругах или возле точки проставляется число данных.
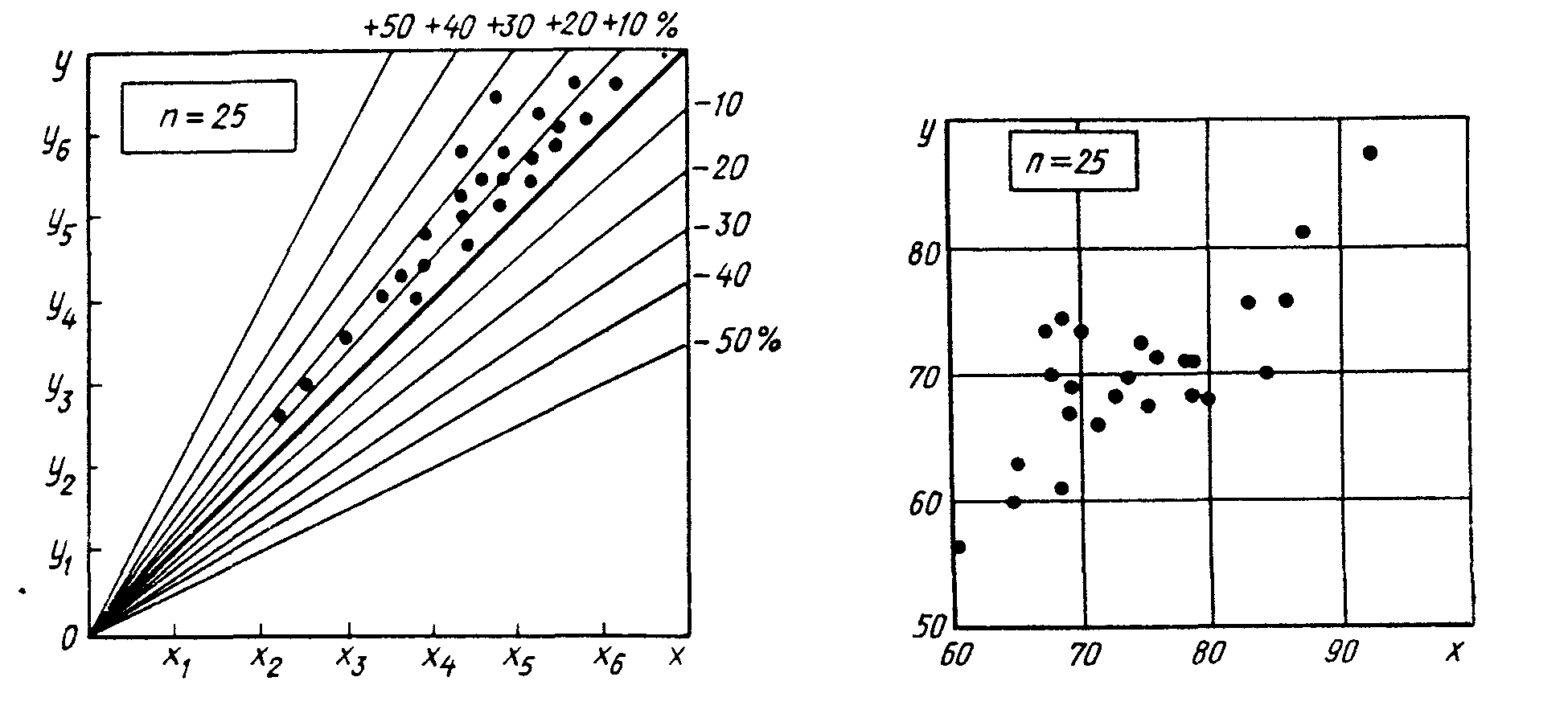
Рис. 3.2. Диаграмма разброса |
Рис. 3.3. Диаграмма разброса данных табл. 3.7 |
Диаграмма разброса позволяет наглядно показать характер изменения параметра качества во времени.
Для этого проведем из начала координат биссектрису. Если все точки лягут на биссектрису, то это означает, что значения данного параметра не изменились в процессе эксперимента. Следовательно, рассматриваемый фактор (или факторы) не влияет на параметр качества.
Если основная масса точек лежит под биссектрисой, то это значит, что значения параметра качества за прошедшее время уменьшились. Если же точки ложатся выше биссектрисы (как в нашем случае на рис. 3.2), то значения параметра за рассматриваемое время возросли.
Проведя лучи из начала координат, соответствующие уменьшению и увеличению параметра на 10, 20, 30, 50, 80%, можно путем подсчета точек между прямыми выяснить частоту значений параметра в интервалах 0...10%, 10...20% и т. д.
Пример 5. Требуется выяснить влияние термообработки интегральных микросхем (ИС) при Т= 120 °С в течение времени t = 24 ч на уменьшение обратного тока р - n-перехода (Iобр).
Для эксперимента было взято 25 интегральных схем (п = 25) и замерены значения Iобр (10-9 А), которые приведены в табл. 3.7.
1. По таблице находят максимальные и минимальные значения х и у: максимальные значения x=92, y=88; минимальные значения х = 60, у = 57.
2. На графике (рис. 3.3) на оси абсцисс откладывают значения х, на оси ординат — значения у. При этом длину осей делают почти равной разности между их максимальными и минимальными значениями и наносят на оси деления шкалы. На вид график приближается к квадрату. Действительно, в рассматриваемом случае разность между максимальными и минимальными значениями равна 92 — 60 = 32 для х и 88 — 57 = 31 для у, поэтому промежутки между делениями шкалы можно делать одинаковыми.
Таблица 3.7
Значения обратного тока р - n-перехода до
и после термообработки ИС
Номер ИС |
До термообработки, x |
После термообработки, у |
Номер ИС |
До термообработки, x |
После термообработки, у |
1 |
68 |
61 |
14 |
75 |
71 |
2 |
71 |
67 |
15 |
73 |
70 |
3 |
65 |
63 |
16 |
69 |
68 |
4 |
78 |
70 |
17 |
73 |
73 |
5 |
75 |
74 |
18 |
73 |
69 |
6 |
85 |
76 |
19 |
83 |
76 |
7 |
86 |
82 |
20 |
70 |
73 |
8 |
84 |
70 |
21 |
68 |
70 |
9 |
74 |
68 |
22 |
79 |
69 |
10 |
65 |
60 |
23 |
78 |
71 |
11 |
78 |
68 |
24 |
78 |
71 |
12 |
92 |
88 |
25 |
73 |
69 |
13 |
60 |
57 |
|
|
|
3. На график наносятся данные в порядке измерений и точки диаграммы разброса.
4. На графике указываются число данных, цель, наименование изделия, название процесса, исполнитель, дата составления графика и т.д. Желательно также, чтобы при регистрации данных во время измерений приводилась и сопровождающая информация, необходимая для дальнейших исследований и анализа: наименование объекта измерения, характеристики, способ выборки, дата, время измерения, температура, влажность, метод измерения, тип измерительного прибора, имя оператора, проводившего измерения (для данной выборки), и др.
С помощью диаграммы разброса можно сравнительно быстро выяснить, имеется ли между двумя рассматриваемыми параметрами корреляционная связь, и, построив методом наименьших квадратов кривую, определить вид этой связи.
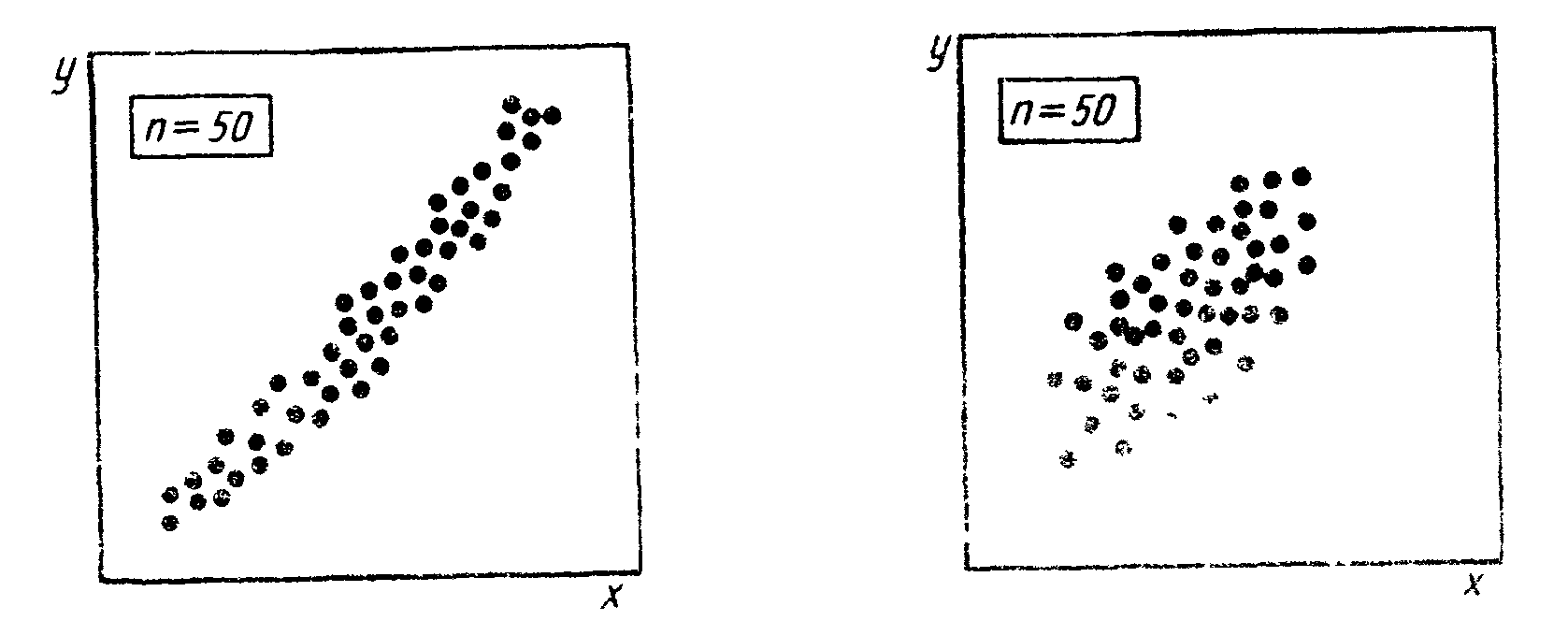
Рис. 3.4. Прямая корреляция |
Рис. 3.5. Легкая прямая корреляция |
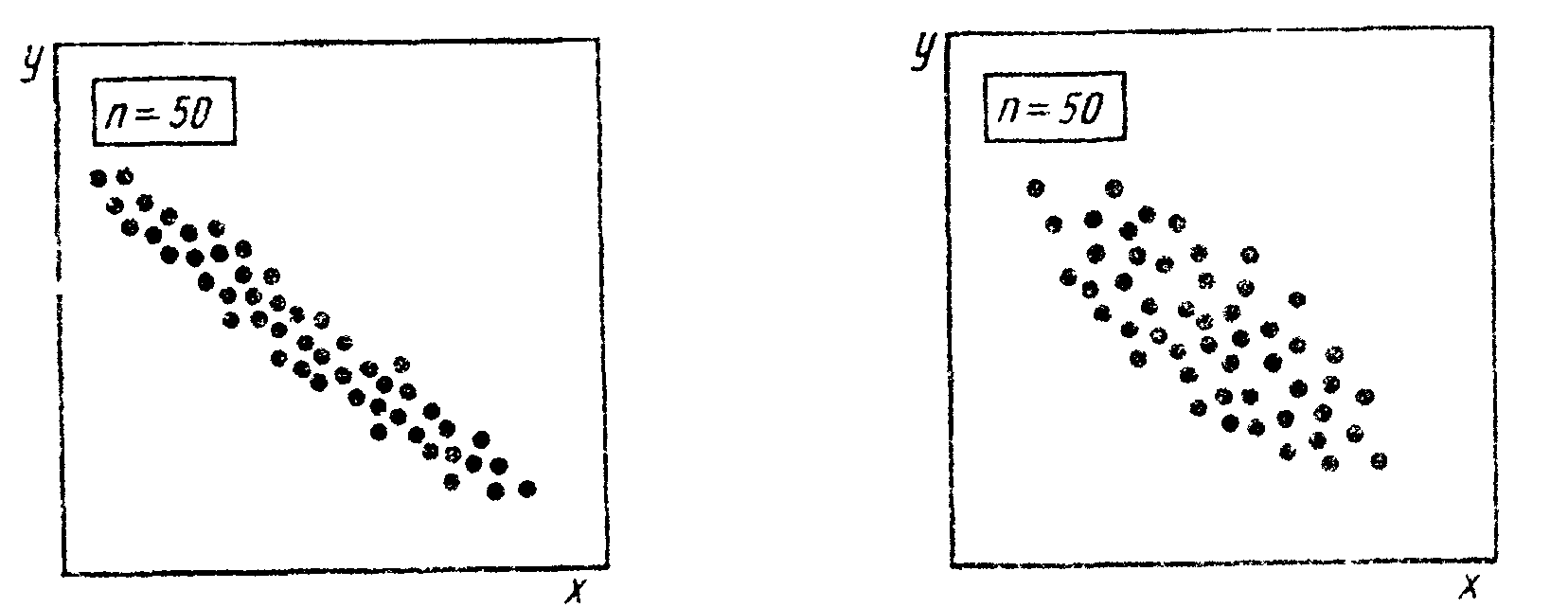
Рис. 3.6. Обратная (отрицательная) корреляция |
Рис. 3.7. Легкая обратная корреляция |
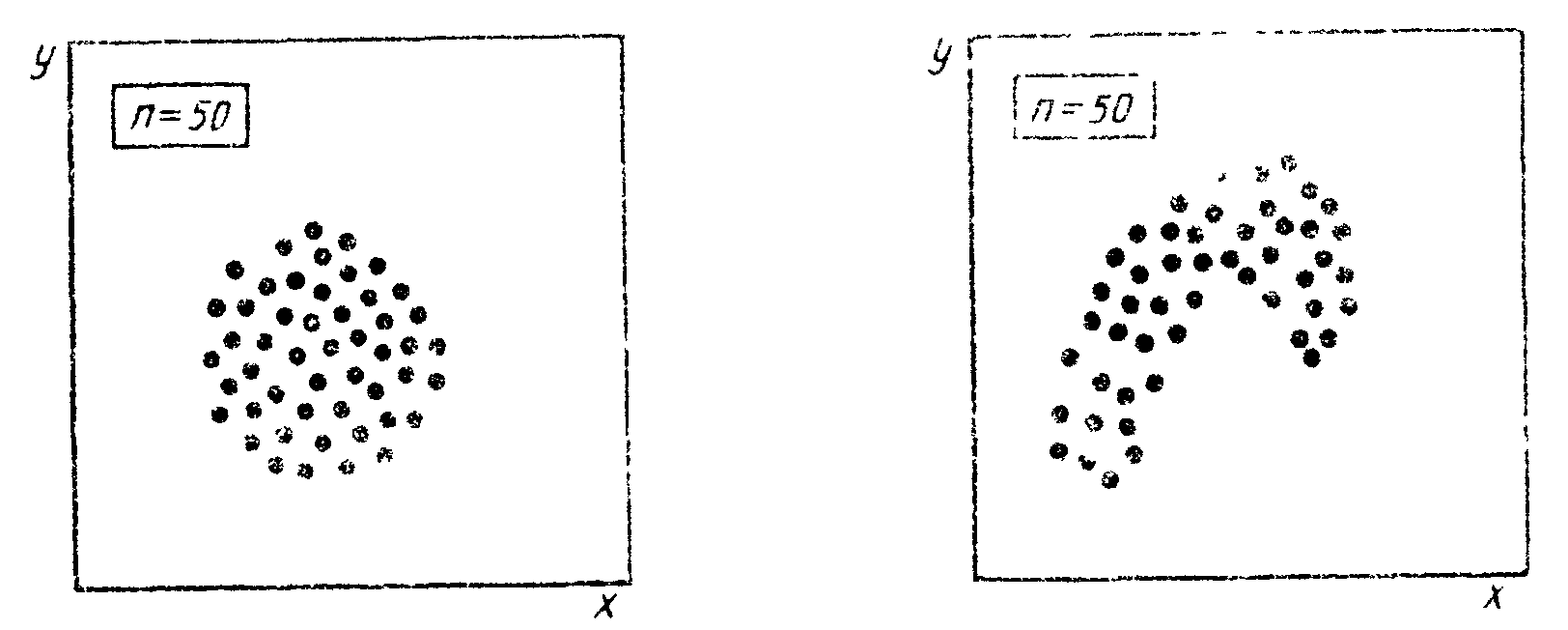
Рис. 3.8. Отсутствие корреляции |
Рис. 3.9. Криволинейная корреляция |
Характер корреляционной зависимости, который определяется видом диаграммы разброса, дает представление о том, каким изменениям будет подвержен один из параметров при определенных изменениях другого. Однако если, как, например, в предыдущем случае (рис. 3.2 и 3.3), для выяснения характера изменения значений параметра качества достаточным было бы число данных порядка 10, то в случае выяснения их корреляционной связи число должно быть значительно больше. Если данных мало, четкую зависимость установить трудно, поэтому желательно, чтобы число пар данных было не меньше 30. Так, на диаграмме рис. 3.4 виден не только характер изменений у в зависимости от изменения х, но и определяется форма связи рассматриваемых признаков в виде уравнения регрессии. На рис. 3.4 четко просматривается прямая корреляция между х и у. В этом случае при осуществлении контроля за причинным фактором х можно управлять значением параметра качества у
На рис. 3.5 приведен пример легкой прямой корреляции. При увеличении х увеличивается также и у, но разброс у велик по отношению к определенному значению х. С помощью контроля причинного фактора х можно до некоторой степени держать под контролем характеристику у, но необходимо также иметь в виду и другие факторы, оказывающие влияние на у.
На рис. 3.6 показан пример обратной (отрицательной) корреляции. При увеличении х характеристика у уменьшается. Если причинный фактор х находится под контролем, характеристика у остается стабильной.
Рис. 3.7 отражает случай легкой обратной корреляции, когда при увеличении x характеристика у уменьшается, но при этом велик разброс значений у, соответствующих фиксированному значению х.
На рис. 3.8 показан пример отсутствия корреляции, когда никакой выраженной зависимости между х и у не наблюдается. В этом случае необходимо продолжить поиск факторов, коррелирующих с у, исключив из этого поиска фактор х.
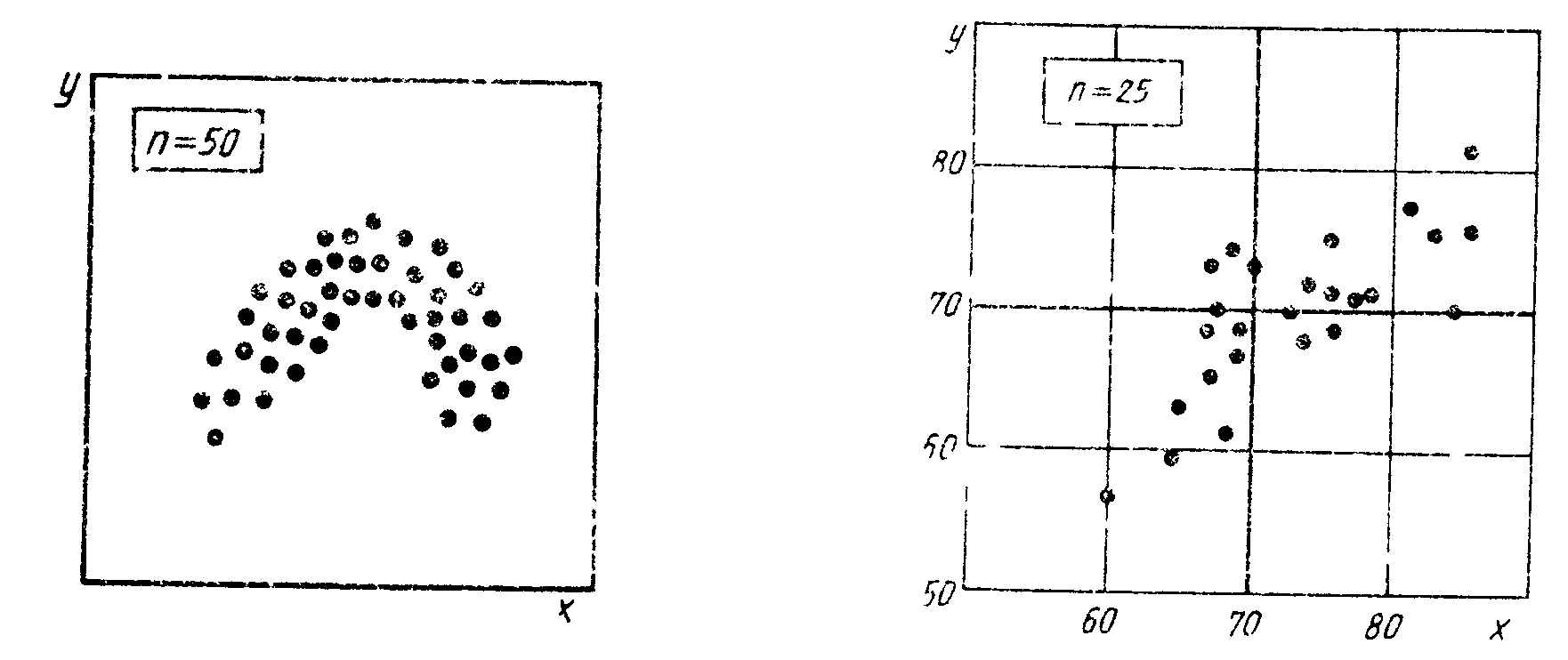
Рис. 3.10. Криволинейная корреляция разброса |
Рис. 3.11. Диаграмма для обратного тока р-n-перехода |
Между параметрами х и у возможны также случаи криволинейной корреляции (рис. 3.9 и 3.10.). Если при этом диаграмму разброса можно разделить на участки, имеющие прямолинейный характер, то проводят такое разделение и исследуют каждые участок в отдельности, как прямолинейную корреляцию.
Степень корреляционной связи х и у может быть оценена либо с помощью коэффициента корреляции (в случае прямолинейной корреляции), либо с помощью коррглзгционного отношения (в случае криволинейной корреляции).
Однако на практике часто применяют более простой метод оценки степени корреляционной связи – метод медиан, особенно удобный при исследовании технологического процесса с использованием данных, полученных на рабочем месте. Рассмотрим действие этого метода на практическом примере, приведенном в табл. 3.7.
1. На диаграмме разброса проводятся вертикальная линия медианы и горизонтальная линия медианы (рис. 3.11). Выше и ниже горизонтальной медианы, справа и слева от вертикальной медианы будет равное число точек. Если число точек окажется нечетным, следует провести линию через центральную точку
2. В каждом из четырех квадратов, получившихся в результате разделения диаграммы разброса вертикальной и горизонтальной медианами, подсчитывают число точек и обозначают их n1 ,п2 , n3, п4 соответственно Точки, через которые прошла медиана, не учитывают.
3. Отдельно складывают точки в положительных и отрицательных квадратах:
n(+) = n1 + n3 =8 + 9 =17,
n(-) = n2 + n4 = 2 + 2 =4,
n’ = n(+) + n(-) = 17 +4 = 21.
Так как четыре точки находятся на медианах, то n’ не равно n = 25.
4. Для определения наличия и степени корреляции по методу медианы используется специальная таблица значений, соответствующих различным коэффициентам риска β (0,01 и 0,05)
Таблица 3.8
Таблица кодовых значений
n' |
β |
n' |
β |
n' |
β |
||||||
0,01 |
0,05 |
0,01 |
0,05 |
|
0,01 |
0,05 |
|||||
8 |
0 |
1 |
38 |
10 |
12 |
68 |
22 |
25 |
|||
9 |
0 |
1 |
39 |
11 |
12 |
69 |
23 |
25 |
|||
10 |
0 |
1 |
40 |
11 |
13 |
70 |
23 |
26 |
|||
11 |
0 |
1 |
41 |
11 |
13 |
71 |
24 |
26 |
|||
12 |
1 |
2 |
42 |
12 |
14 |
72 |
24 |
27 |
|||
13 |
1 |
2 |
43 |
12 |
14 |
73 |
25 |
27 |
|||
14 |
1 |
2 |
44 |
13 |
15 |
74 |
25 |
28 |
|||
15 |
2 |
3 |
45 |
13 |
15 |
75 |
25 |
28 |
|||
16 |
2 |
3 |
46 |
13 |
15 |
76 |
26 |
28 |
|||
17 |
2 |
4 |
47 |
14 |
16 |
77 |
26 |
29 |
|||
18 |
3 |
4 |
48 |
14 |
16 |
78 |
27 |
29 |
|||
19 |
3 |
4 |
49 |
15 |
17 |
79 |
27 |
30 |
|||
20 |
3 |
5 |
50 |
15 |
17 |
80 |
28 |
30 |
|||
21 22 |
4 4 |
5 5 |
51 52 |
15 16 |
18 18 |
81 82 |
28 28 |
31 31 |
|||
23 24 |
4 5 |
6 6 |
53 54 |
16 17 |
18 9 |
83 84 |
29 29 |
32 32 |
|||
25 26 |
5 б |
7 7 |
55 56 |
17 17 |
19 20 |
85 86 |
30 30 |
32 33 |
|||
27 28 |
6 6 |
7 8 |
57 58 |
18 18 |
20 21 |
87 88 |
31 31 |
33 34 |
|||
29 |
7 |
8 |
59 |
19 |
21 |
89 |
31 |
34 |
|||
30 |
7 |
9 |
60 |
19 |
21 |
90 |
32 |
35 |
|||
31 |
7 |
9 |
61 |
20 |
22 |
|
|
|
|||
32 |
8 |
9 |
62 |
20 |
22 |
|
|
|
|||
33 |
8 |
10 |
63 |
20 |
23 |
|
|
|
|||
34 |
9 |
10 |
64 |
21 |
23 |
|
|
|
|||
35 |
9 |
11 |
65 |
21 |
24 |
|
|
|
|||
36 |
9 |
11 |
66 |
22 |
24 |
|
|
|
|||
37 |
10 |
12 |
67 |
22 |
25 |
|
|
|
|||
Сравнивая меньшее из чисел n(+) и n(-) с их кодовым значением из табл. 3.8, соответствующим значению n', делают заключение о наличии и характере корреляции. Если меньшее из чисел n(+) и n(-) оказывается равным или меньше табличного кодового значения, то корреляционная зависимость имеет место. В рассматриваемом примере табличное кодовое значение при коэффициенте риска β=0,01, соответствующее п'=21, равно 4. Меньшим из чисел n(+) = 17 и n(-) =4 является n(-). Поскольку n(-), равное 4, оказывается равным кодовому значению 4, можно утверждать, что в данном случае между двумя параметрами существует корреляционная зависимость. Это утверждение делается с вероятностью ошибиться только в одном случае из ста (β =0,01). Поскольку n(+)>n(-) ,это свидетельствует о прямой корреляции. В тех случаях, когда n(+)<n(-), можно говорить об обратной корреляции.
Путем сдвига во времени значений одного параметра относительно соответствующих значений другого рассматриваемого параметра можно получить более конкретную информацию о воздействующих факторах.
Пример 6. Число рекламаций по месяцам на однотипные изделия А и B, изготовленные различными предприятиями и поступившие на фирму, занимающуюся сборкой ЭС, приведены в табл. 3.9.
Если построить диаграмму разброса (рассеяния), то она будет иметь вид, приведенный на рис. 3.12.
Расположив соответствующие рекламации в упорядоченные ряды (х: 100, 102, 105, 108, 112, 115, 116, 118, 120, 125, 125, 128; у: 65, 66, 68, 69, 70, 71, 75, 76, 77, 78, 79, 82), нетрудно убедиться, что медианные значения соответственно равны Меx=115, 5 и Меy= 73. Проведя горизонтальную и вертикальную линии медиан, подсчитаем число точек в каждом квадранте.
Таблица 3.9
Число рекламаций по изделиям А и В
Месяц |
Число рекламаций на изделие А (х) |
Число рекламаций на изделие В (у) |
1 |
105 |
68 |
2 |
102 |
71 |
3 |
100 |
69 |
4 |
108 |
66 |
5 |
112 |
65 |
б |
115 |
70 |
7 |
118 |
75 |
8 |
116 |
76 |
9 |
120 |
78 |
10 |
125 |
77 |
11 |
125 |
79 |
12 |
128 |
82 |
Как видно из рис. 3.12, все точки расположены только в положительных (в первом и третьем) квадрантах, т. е.
n(+) = n1 + n3 =6 + 6 =12,
n(-) = n2 + n4 = 0 + 0 =0,
n’ = n(+) + n(-) = 12.
По табл. 3.8 для n'= 12 и β=0,01 кодовое значение равно 1. Так как меньшее из чисел n(+) и n(-) является n(-) =0 и оно меньше кодового значения, то корреляционная зависимость имеет место. Поскольку n(+)>n(-), это свидетельствует о прямой корреляции. Если подсчитать коэффициент корреляции по формуле (2.64), то можно убедиться, что имеет место довольно высокая корреляция (z=0,81).
При рассмотрении табл. 3.9 становится ясно, что значения х (x1 ,x2 , х3 , ..., х12) соответствуют значениям у (y1 ,у2 ,…, у12). При этом мы рассматриваем соответствие (х1,у1), .... (x12, y12).
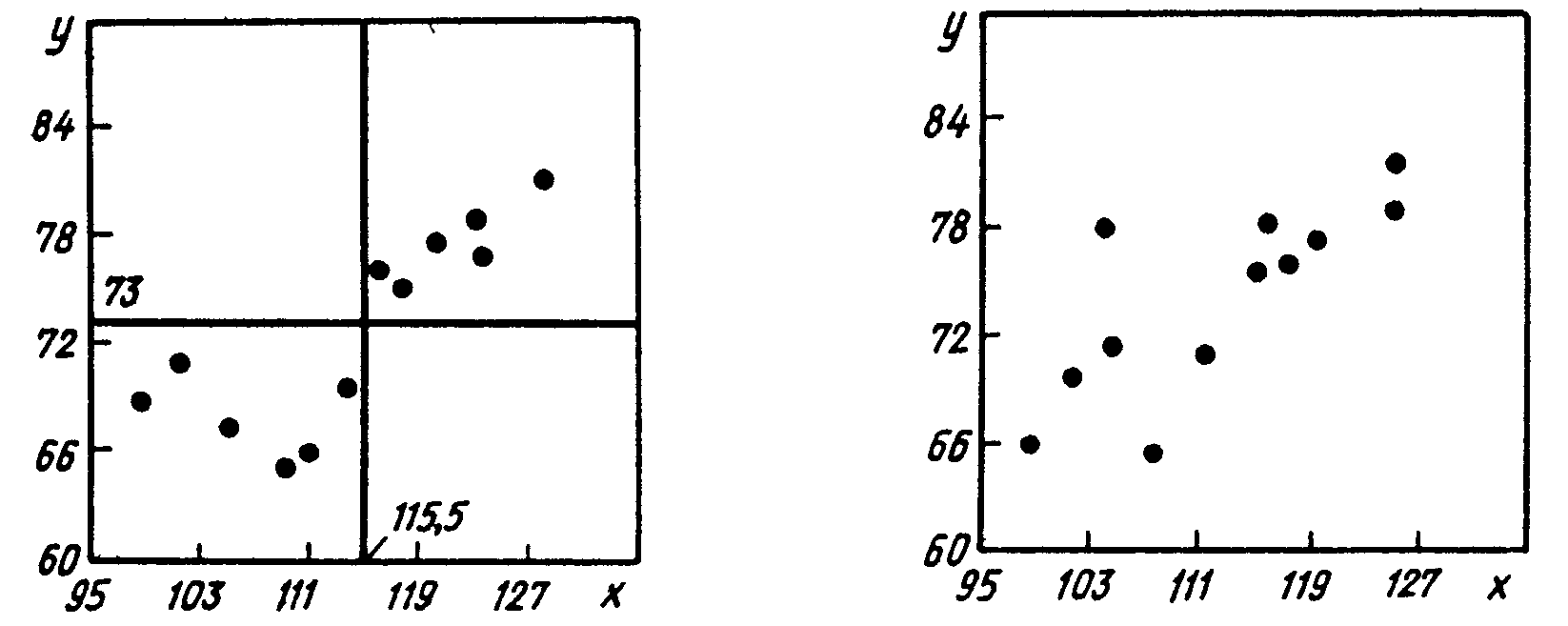
Рис. 3.12 Диаграмма разброса для числа рекламаций по изделиям А и В |
Рис. 3.13. Диаграмма разброса с лагом в 1 месяц |

Рис. 3.14. Диаграмма разброса с лагом в 2 месяца |
Рис. 3.15. Диаграмма разброса с лагом в 3 месяца |
А что получится, если это соответствие сдвинуть? Если, например, имеет место смещение на один месяц, т. е. (xl, y2), {хг, у3),...., (x11, y12) то диаграмма разброса будет иметь вид, приведенный на рис. 3.13.
Подобный временной сдвиг называют временным лагом. Таким образом, диаграмма рис. 3.13 — это диаграмма разброса с временным лагом в 1 месяц.
Если задать временной лаг в 2 и 3 месяца, то получим соответственно диаграммы рис. 3.14 и 3.15.
Из сравнения диаграмм видно, что наивысшая корреляция достигается при временном лаге в 2 месяца (на рис. 3.14 точки группируются более явно около прямой, чем на рис. 3.15). Иными словами, рекламации на изделия В хорошо коррелируют с рекламациями на изделие А, пришедшими за 2 месяца до них. Именно в это время нужно выявлять факторы, влияющие на качество изделий.
При временном лаге может возникнуть проблема определения числа рекламаций в будущем. Так, для временного лага в 2 месяца необходимо определить число рекламаций у13 на изделие В в 13-м месяце. Для этого используют прямую регрессии и формулу (2.62). Если в формуле (2.62) заменить коэффициент регрессии b на коэффициент корреляции r [см. формулу (2.64)], то она приобретает следующий вид:
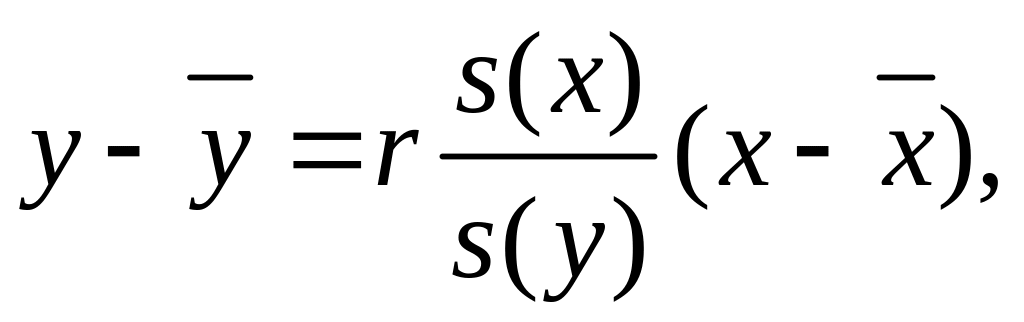 (3.1)
(3.1)
где s(x) и s(y) определяются по формуле (2.10) соответственно для - значений х и у.
Тогда, если вычислить , , s(x), s(y), r, можно найти предсказанные значения (прогноз) у для заданного значения х.
Попробуем предсказать и значения у13 ,числа рекламаций на изделие В в 13-м месяце при временном лаге в 2 месяца, пользуясь данными табл. 3.9.
Коэффициент корреляции при временном лаге в 2 месяца составляет z=0,99, а из расчетов получаем:
=112,1; s(x)= 7.76,
=73,7; s(y)= 5,51.
По формуле прямой регрессии (3.1) получаем
![]() (3.2)
(3.2)
При временном лаге в 2 месяца значение у13 для изделия В (за 13-й месяц) при x11 =125 по формуле (3.2) составит у13 = 82,8.
