
- •Фгбоу впо “Воронежский государственный технический университет”
- •Ответственный за выпуск зав. Кафедрой д-р техн. Наук, проф. А.И. Шиянов
- •1. Цель работы
- •2. Теоретические сведения
- •2.1. Основные понятия и определения
- •2.5. Энергетический баланс в электрических цепях
- •3. Программа лабораторной работы
- •3.1. Описание лабораторного стенда
- •3.3. Программа работы
- •3.3.1. Исследование цепи при последовательном соединении элементов
- •4. Контрольные вопросы
- •2.1. Основные параметры синусоидальных величин
- •2.4. Мощности цепи переменного тока
- •2.9. Цепь с последовательным соединением элементов r, l, c
- •2.10. Резонанс напряжений
- •3. Программа лабораторной работы
- •3.3.2. Определение параметров конденсатора
- •3.3.3. Исследование цепи с последовательным соединением r, l, с элементов
- •4. Контрольные вопросы
2.9. Цепь с последовательным соединением элементов r, l, c
С хема
цепи изображена на рис. 2.15. Мгновенное
напряжение цепи u
равно сумме мгновенных напряжений uR,
uL,
uC
на соответствующих элементах цепи
хема
цепи изображена на рис. 2.15. Мгновенное
напряжение цепи u
равно сумме мгновенных напряжений uR,
uL,
uC
на соответствующих элементах цепи
![]() .
.
При синусоидальном напряжении u ток i также синусоидален и, в общем случае, сдвинут на угол φ относительно напряжения. При заданном напряжении задачей расчета цепи является определение величины тока и угла φ.
Для комплексов действующих напряжений и токов (см. рис. 2.15) запишем:
 (2.49)
(2.49)
где
![]() – комплексное сопротивление.
– комплексное сопротивление.
В соответствии с (2.49).
![]() (2.50)
(2.50)
где
![]() – реактивное сопротивление;
– реактивное сопротивление;
z и – модуль и аргумент комплексного сопротивления.
В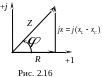 свою очередь
свою очередь
![]() ,
(2.51)
,
(2.51)
![]() .
(2.52)
.
(2.52)
Исходя из (2.50), можно построить треугольник сопротивлений (рис. 2.16). Выражения (2.51), (2.52) можно легко получить с помощью рис. 2.16.
В соответствии с (2.49) комплексный ток вычисляется по закону Ома в комплексной форме:
![]() . (2.53)
. (2.53)
Если мгновенное напряжение
![]() ,
,
то комплекс действующего напряжения
![]() .
.
Исходя из (2.50) (2.53)
![]() ,
(2.54)
,
(2.54)
где
![]() – действующее значение тока в цепи.
– действующее значение тока в цепи.
Величина φ определяет сдвиг фаз между напряжением и током. Исходя из (2.54), для мгновенного тока запишем:
![]() .
(2.55)
.
(2.55)
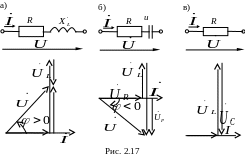
Если xL
> xC,
цепь для определения тока можно заменить
последовательным соединением сопротивления
R и индуктивного
сопротивления
![]() = xL
– xC
(рис. 2.17, а). При этом угол φ в (2.50)
положителен и ток отстает от напряжения
на угол φ.
= xL
– xC
(рис. 2.17, а). При этом угол φ в (2.50)
положителен и ток отстает от напряжения
на угол φ.
Если xL
< xC,
цепь можно заменить эквивалентным
сопротивлением, состоящим из активного
сопротивления R и
емкостного сопротивления
![]() рис. 2.17, б. При этом величина φ в
(2.50) отрицательна, и ток опережает
напряжение на угол φ.
рис. 2.17, б. При этом величина φ в
(2.50) отрицательна, и ток опережает
напряжение на угол φ.
Если xL = xC, цепь для расчета тока замещается сопротивлением R (рис. 2.17, в).
Если принять начальную фазу тока за
ноль, то для трех случаев эквивалентных
сопротивлений можно построить
соответствующие векторные диаграммы
(рис. 2.17). Разность между векторами
и
![]() обозначена как напряжение
обозначена как напряжение
![]() на эквивалентном сопротивлении.
на эквивалентном сопротивлении.
Треугольник, образованный векторами
![]()
![]() и
называют треугольником
напряжений. Он сходен с треугольником
сопротивлений. В рассмотренной цепи
напряжения
и
на реактивных
элементах могут превышать входное
напряжение U.
и
называют треугольником
напряжений. Он сходен с треугольником
сопротивлений. В рассмотренной цепи
напряжения
и
на реактивных
элементах могут превышать входное
напряжение U.
П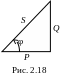 олная
S, активная Р и
реактивная мощности определяются из
выражений
олная
S, активная Р и
реактивная мощности определяются из
выражений
,
![]() ,
,
![]() ,
,
![]() .
.
Треугольник мощностей (рис. 2.18), сходен с треугольниками сопротивлений и напряжений. Величину cos φ = P / S называют коэффициентом мощности.
2.10. Резонанс напряжений
Если электрическая цепь имеет одну или несколько индуктивностей и одну или несколько емкостей, то возможен резонансный режим – когда эквивалентное сопротивление цепи (входное сопротивление) является чисто активным, и входные напряжение и ток совпадают по фазе. Различают две разновидности резонанса – резонанс напряжений и резонанс токов.
Резонанс напряжений имеет место при последовательном соединении индуктивности и емкости (рис. 2.15). В соответствии с (2.50) эквивалентное сопротивление цепи является чисто активным, когда xL = xC. Таким образом, условие резонанса
![]() ,
(2.56)
,
(2.56)
где 0 – резонансная частота.
Исходя из (2.56)
![]()
![]() .
(2.57)
.
(2.57)
При частоте 0 напряжения на индуктивности и емкости равны, поэтому используют термин “резонанс напряжений”.
Векторная диаграмма, соответствующая резонансу напряжений, приведена на рис. 2.17, в.
Добротность резонансного контура
![]() .
(2.58)
.
(2.58)
Величина Q показывает, во сколько раз напряжение на реактивном элементе превышает входное напряжение в резонансном режиме. В радиотехнических устройствах Q может достигать 300 и более.
И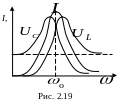 сходя
из (2.58), резонанс можно получить путем
изменения одной из трех величин: частоты,
индуктивности или емкости. Зависимость
напряжений и токов цепи от изменяемого
параметра называют резонансными
характеристиками. Данные характеристики
при изменении частоты приведены на рис.
2.19.
сходя
из (2.58), резонанс можно получить путем
изменения одной из трех величин: частоты,
индуктивности или емкости. Зависимость
напряжений и токов цепи от изменяемого
параметра называют резонансными
характеристиками. Данные характеристики
при изменении частоты приведены на рис.
2.19.
Зависимость тока от частоты определяется формулой
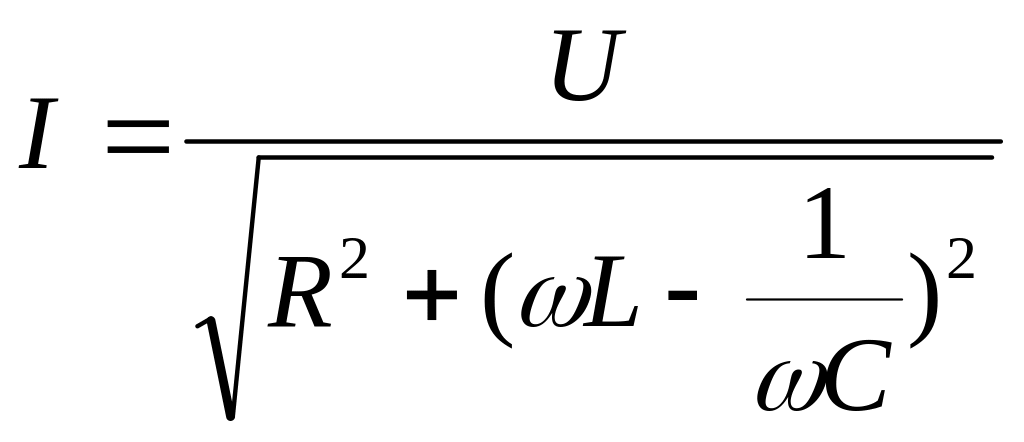 .
(2.59)
.
(2.59)
В режиме резонанса ток максимален.
Максимальные значения напряжений
![]() и
и
![]() имеют место при
имеют место при
![]() .
.
