2.4. Мощности цепи переменного тока

Мгновенная мощность источника переменного напряжения

. (2.14)

Если

(2.15)

то

(2.16)

В соответствии с (2.15) и (2.16) можно представить графики на рис 2.6.

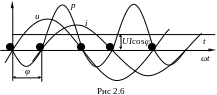
Мощность р имеет постоянную и переменную составляющие. При значениях р, лежащих ниже оси абсцисс, энергия отдаётся в источник напряжения, на остальных участках энергия потребляется от источника.

Постоянная составляющая потребляемой мощности Р – это среднее значение мощности за период:

(2.17)

Мощность Р называют активной мощностью, а cos – коэффициентом мощности. Активную мощность измеряют в ваттах (Вт). Используют также понятия полной мощности S и реактивной мощности Q:

(2.18)

(2.19)

Реактивную мощность измеряют в вольт-амперах реактивных (ВАр), а полную мощность – в вольт-амперах (ВА).

Рассмотренные мощности связаны соотношением:

(2.20)

Г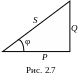 рафически это представляется треугольником мощностей (рис. 2.7).

На щитках источников электрической энергии (трансформаторы, генераторы) указывают номинальное значение S . Величина S характеризует мощность, которую источник может длительно отдавать потребителю при

2.5. Основные понятия о символическом (комплексном) методе

Метод основан на операциях с комплексными числами, символически изображающими синусоидально изменяющиеся величины.

К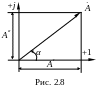 омплексное число изображают в виде вектора на комплексной плоскости (рис. 2.8).

Данное число можно записать в алгебраической, показательной и тригонометрической формах:

где и – вещественная и мнимая части;

– мнимая единица;

А – модуль; α – аргумент.

Положительное значение α отсчитывается от вещественной оси против часовой стрелки.

Величины и являются ортогональными координатами вектора , а А и α – полярными. С учетом рис. 2.8

.

Алгебраическая форма удобна при сложении комплексных чисел, показательная – при умножении, делении, возведении в степень.

Рассмотрим сложение двух комплексных чисел и .

Пусть и .

Тогда .

Э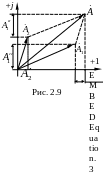 тому соответствует рис. 2.9.

Пусть тогда при умножении получим

При делении этих векторов имеем

При возведении в степень имеем .

При извлечении корня n-ой степени справедливо выражение .

Умножение вектора на j приводит к его повороту на 90˚ против часовой стрелки.

Пусть мгновенное напряжение равно

. (2.21)

Рассмотрим вектор (комплексное число)

(2.22)

Таким образом, напряжение u можно рассматривать как

мнимую часть вектора

Вектор вращается со скоростью ω против часовой

стрелки. Векторы синусоидально изменяющихся величин принято изображать на комплексной плоскости для момента времени t = 0. В этом случае (2.22) запишется как

(2.23)

В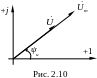 ектор считают комплексной амплитудой напряжения и изображают на комплексной плоскости в виде рис. 2.10.

Комплекс действующего напряжения

, (2.24)

где U – действующее значение напряжения.

Величину часто называют комплексным напряжением.

Аналогичным образом изображаются и векторы токов.

2.6. Активное сопротивление при синусоидальном токе

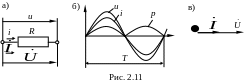
Если к сопротивлению R (рис. 2.11) приложено синусоидальное напряжение u, то в нем протекает синусоидальный ток, совпадающий по фазе с напряжением:

(2.25)

(2.26)

Исходя из (2.25), (2.26), комплексы действующих напряжений и тока

, , (2.27)

где и ­–­­ действующие значения напряжения и тока.

Векторы напряжения и тока совпадают по направлению (по фазе) – рис. 2.11, в.

Для активного сопротивления можно записать закон Ома в комплексной форме:

. (2.28)

При протекании тока через сопротивление R на нём возникает падение напряжения – рис. 2.11, а.

Мгновенная мощность р, выделяющаяся в активном сопротивлении, есть функция времени:

(2.29)

Средняя за период Т мощность, выделяющаяся в сопротивлении R (активная мощность):

. (2.30)

Из (2.30), в частности, следует, что активная мощность в сопротивлении R пропорциональна квадрату действующего значения тока.

Выражение можно также получить из (2.17) с учетом того, что и . При этом полная мощность , а реактивная мощность .

2.7. Идеальная индуктивность при синусоидальном токе

При протекании тока через любые элементы создаётся магнитное поле. Связь между током i_L и энергией магнитного поля W_L характеризуется индуктивностью L:

(2.31)

Таким образом, индуктивности накапливают энергию магнитного поля.

Единица измерения индуктивности [Гн] – генри:

.

При изменении тока в индуктивности наводится ЭДС самоиндукции

(2.32)

При протекании синусоидального тока

(2.33)

в индуктивности наводится ЭДС самоиндукции

. (2.34)

Напряжение u_L, приложенное к индуктивности (рис. 2.12, а), противоположно ЭДС.

(2.35)

Таким образом, синусоидальный ток в индуктивности отстаёт от напряжения на 90˚ – рис. 2.12, б.

Для действующих значений напряжения и тока запишем:

(2.36)

где – индуктивное сопротивление, измеряемое в Ом.

Так как ток отстаёт от напряжения на 90˚ в символической форме можно записать:

(2.37)

Комплексное индуктивное сопротивление

(2.38)

Векторы напряжения и тока сдвинуты на комплексной плоскости на 90˚ – рис 2.12, в.

Мгновенная мощность индуктивности

. (2.39)

При увеличении тока энергия поступает от источника питания (см. рис. 2.12, б) и преобразуется в энергию магнитного поля. При уменьшении тока энергия, запасенная в магнитном поле, отдается в источник. Активная мощность (средняя за период мощность, потребляемая от сети) равна нулю:

Полная мощность S равна реактивной мощности Q:

Таким образом, при питании идеальной индуктивности синусоидальным напряжением происходит периодический обмен энергией между источником питания и индуктивностью, но в среднем потребляемая индуктивностью мощность равна нулю.

И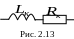 ндуктивности реализуются в виде катушек индуктивности. Такие катушки кроме индуктивности имеют активное сопротивление. Катушки индуктивности характеризуют последовательным соединением индуктивности и сопротивлением – рис. 2.13.

2.8. Цепь с идеальной емкостью

Элементы, реализующие емкость – конденсаторы, обозначение которых показано на рис. 2.14, а.

Конденсаторы накапливают энергию электрического поля:

. (2.40)

Ток конденсатора:

. (2.41)

Напряжение на конденсаторе:

(2.42)

Если напряжение конденсатора

, (2.43)

то его ток

. (2.44)

Таким образом, ток конденсатора на 90º опережает его напряжение – рис 2.14, б. Исходя из (2.44), для действующих значений напряжения и тока, запишем:

, (2.45)

где – емкостное сопротивление.

Так как ток на 90º опережает напряжение, в символической форме можно записать:

. (2.46)

Комплексное емкостное сопротивление:

. (2.47)

Мгновенная мощность конденсатора:

. (2.48)

При увеличении напряжения (рис. 2.14, б) энергия потребляется от источника питания, при уменьшении – отдается в источник. Мощности идеального конденсатора:

, , .