Фгбоу впо “Воронежский государственный технический университет”

Кафедра робототехнических систем

ИССЛЕДОВАНИЕ ЦЕПЕЙ ПОСТОЯННОГО И ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторным работам № 1, 2 по дисциплине

“Электротехника” для студентов направления подготовки

бакалавров 221000 «Мехатроника и робототехника»

(профиль «Промышленная и специальная робототехника»)

очной формы обучения

Воронеж 2012

Составители: канд. техн. наук А.К. Муконин,

канд. техн. наук В.А. Медведев

УДК 621.3

Исследование цепей постоянного и однофазного синусоидального тока: методические указания к лабораторным работам № 1, 2 по дисциплине “Электротехника” для студентов направления подготовки бакалавров 221000 «Мехатроника и робототехника» (профиль «Промышленная и специальная робототехника») очной формы обучения / ФГБОУ ВПО “Воронежский государственный технический университет”; сост. А.К. Муконин, В.А. Медведев. Воронеж, 2012. 37 с.

Методические указания содержат теоретические сведения об основных понятиях и законах теории электрических цепей, мощности и энергетическом балансе в электрических цепях, расчете цепей постоянного и однофазного синусоидального тока. Сформулированы программы лабораторных работ и контрольные вопросы.

Методические указания предназначены для студентов 2 курса. Они будут полезны студентам при выполнении лабораторных работ и углубленном изучении лекционного материала.

Табл. 1. Ил. 35. Библиогр.: 1 назв.

Рецензент канд. техн. наук, доц. В.А. Трубецкой

Ответственный за выпуск зав. Кафедрой д-р техн. Наук, проф. А.И. Шиянов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

с ФГБОУ ВПО “Воронежский

государственный технический университет”, 2012

Лабораторная работа № 1

ИССЛЕДОВАНИЕ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

1. Цель работы

Изучение основных сведений об электрических цепях постоянного тока. Расчет и исследование неразветвленной и разветвленной цепей постоянного тока.

2. Теоретические сведения

2.1. Основные понятия и определения

Электрическая цепь – совокупность соединенных друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток. Для описания электромагнитных процессов в электрических цепях используют понятия: “ток”, “напряжение”, “электродвижущая сила” (ЭДС), “активное сопротивление”, “проводимость”, “индуктивность”, “емкость”, “мощность” и др. Мгновенные значения тока, напряжения, ЭДС и мощности обычно обозначают строчными (малыми) буквами, соответственно i, u, e, p. Активное сопротивление обозначают буквами R или r, проводимость – q. В системе Си ток измеряют в амперах (А), напряжение и ЭДС – в вольтах (В), сопротивление – в омах (Ом), проводимость – в сименсах (См), мощность в ваттах (Вт). Проводимость – величина, обратная сопротивлению .

В названии “активное сопротивление” слово “активное” обычно опускают. Активное сопротивление во многих случаях называют резистивным сопротивлением, а элемент, реализующий такое сопротивление – резистором.

Носителями зарядов в металлах являются свободные электроны, а в жидкостях и ионизированных газах – ионы. Упорядоченное движение носителей заряда под действием электрического поля называют электрическим током. Мгновенное значение тока

, (2.1)

где q – заряд, измеряемый в кулонах (Кл).

Соответственно 1 А = 1 Кл / c.

Постоянным током называют ток, постоянный во времени. Обозначают постоянный ток прописной буквой I. Соответственно постоянное напряжение, ЭДС и мощность обозначают прописными буквами U, E и P.

З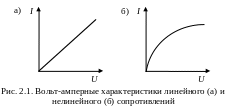 ависимость тока в сопротивлении (нагрузке) от напряжения на этом сопротивлении – вольт-амперная характеристика (ВАХ). Сопротивление называют линейным, если его ВАХ – прямая (рис. 2.1, а), и нелинейным, если его ВАХ – кривая (рис. 2.1, б).

Электрические цепи, содержащие только линейные сопротивления, называют линейными, цепи хотя бы с одним нелинейным элементом – нелинейными.

Ниже рассматриваются линейный цепи.

Напряжение на участке цепи равно разности потенциалов между крайними точками этого участка.

Н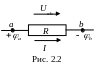 а рис. 2.2 приведен пример цепи, содержащей сопротивление R. Напряжение на сопротивлении, то есть между точками a и b,

,

где _а и _b – потенциалы точек a и b.

Закон Ома для участка цепи, не содержащего источников электрической энергии, устанавливает связь между напряжением и током на этом участке. Такой участок цепи можно представить в виде эквивалентного сопротивления R (рис. 2.2). В этом случае закон Ома

. (2.2)

Ток протекает от более высокого потенциала _а к более низкому потенциалу _b.

Величину U_ab = IR называют напряжением на сопротивлении или падением напряжения на сопротивлении.

Источники ЭДС и источники тока. Источники электрической энергии (ИЭЭ) в цепях постоянного тока имеют два вывода (положительный и отрицательный). Напряжение U между этими выводами зависит от тока I источника. Названную зависимость называют внешней характеристикой источника энергии.

В линейных цепях внешняя характеристика линейна (рис. 2.3, а). В таком случае ИЭЭ характеризуют величиной ЭДС Е и внутренним сопротивлением R_B.

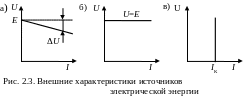
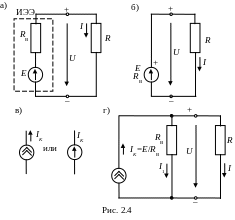
В схемах такой источник изображают в виде последовательного соединения R_B и идеального источника ЭДС Е, обозначаемого в виде окружности со стрелкой (рис. 2.4, а) Стрелка направлена от вывода с меньшим потенциалом к выводу с большим потенциалом. Второй вариант изображения рассматриваемого источника приведен на рис. 2.4, б, где символ R_B показывает, что источник ЭДС имеет внутреннее сопротивление.

Уравнение внешней характеристики источника

. (2.3)

То есть выходное напряжение меньше ЭДС Е на величину падения напряжения на внутреннем сопротивлении (см. рис. 2.3, а). В режиме холостого хода, когда нагрузка R отключена и ток равен нулю, . Отсюда следует, что на практике ЭДС можно определить, измерив напряжение ИЭЭ в режиме холостого хода.

Совокупность идеального источника ЭДС и внутреннего сопротивления R_B называют реальным источником ЭДС или источником напряжения.

Уравнение (2.3) имеет два крайних случая. В первом случае , то есть ИЭЭ идеальный источник ЭДС, напряжение на выходе которого не зависит от тока – рис. 2.3, б. Во втором случае , , . Такой источник питания называют источником тока и обозначают в виде символов, приведенных на рис. 2.4, в. Внешняя характеристика источника тока приведена на рис. 2.3, в.

Очевидно, что идеального источника тока не существует, но понятие об источнике тока применяется в ряде случаев для расчета электрических цепей. В частности, ИЭЭ, имеющий характеристику в виде рис. 2.3, а, то есть характеризующийся ЭДС Е и внутренним сопротивлением R_B, можно представить не только в виде рис. 2.4, а, но и в виде рис. 2.4, г. Источник ЭДС с внутренним сопротивлением R_B заменяется источником тока, шунтированным сопротивлением R_B. Ток источника тока .

Покажем, что ток I и напряжение U нагрузки R в схемах на рис. 2.4, а и рис. 2.4, г одинаковы. Для схемы рис. 2.4, а

; .

Предположим, что в схеме рис. 2.4, г напряжение . Отсюда

; ; .

Это свидетельствует об эквивалентности рассматриваемых схем.

Неразветвленные и разветвленные электрические цепи. В электрических цепях принято выделять ветви, узлы, контуры.

Ветвь – участок цепи между двумя узлами, состоящий из последовательно соединенных элементов, в которых течет один и тот же ток.

Узел – место соединения не менее трех ветвей (место соединения выделяется точкой).

Контур – замкнутый путь, в котором один узел является началом и концом пути.

Независимый контур – контур, содержащий хотя бы один элемент, не принадлежащий другим контурам.

Неразветвленная цепь имеет один контур. Пример неразветвленной цепи приведен на рис. 2.4, а.

Разветвленная цепь содержит не менее двух контуров.

Р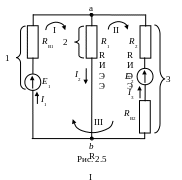 азветвленная цепь на рис. 2.5 имеет два узла a и b, три ветви 1, 2, 3 и три контура I, II, III. Контур I включает ветви 1, 2. Контур II – ветви 2, 3. Контур III – ветви 1 и 3. Независимыми являются два любых контура из трех.

2.2. Законы Кирхгофа и Ома

Первый закон Кирхгофа применяется к узлам схемы и формулируется двояко:

1. Сумма токов, текущих к узлу, равна сумме токов, текущих от узла.

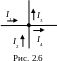2. А лгебраическая сумма токов в ветвях узла равна нулю, то есть

, (2.4)

где токи, направленные к узлу, берут с одним знаком, а направленные от узла – с другим.

Для узла на рис. 2.6 можно записать .

Второй закон Кирхгофа применяется к контурам схемы и формулируется в виде: алгебраическая сумма падений напряжений на сопротивлениях замкнутого контура равна алгебраической сумме ЭДС этого контура:

, (2.5)

где положительные знаки применяются для токов и ЭДС, направления которых совпадают с произвольно выбранным направлением обхода контура.

К примеру для контура III на рис. 2.5 можно записать:

. (2.6)

Закон Ома для участка цепи (ветви) с источниками ЭДС позволяет определить ток ветви по разности потенциалов U_ab на концах ветви и имеющимся в ветви ЭДС и сопротивлениям:

(2.7)

где – алгебраическая сумма ЭДС (знак “плюс” берется для ЭДС, совпадающей по направлению с искомым током);

– сумма сопротивлений ветви.

К примеру, для участка цепи на рис. 2.7

.

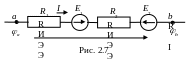Знак тока I можно выбрать произвольно. Если рассчитанное значение I отрицательно, то направление тока противоположно выбранному.

Закон Ома для замкнутой неразветвленной цепи:

, (2.8)

где – алгебраическая сумма ЭДС цепи (знак “плюс” берется для ЭДС, совпадающих по направлению с током);

– сумма сопротивлений.

В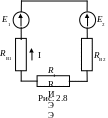 принципе, направление тока в цепи можно выбрать произвольно. Если при этом отрицательна, то реальное направление тока противоположно выбранному.

К примеру, для схемы на рис. 2.8

.

Если , то направление тока выбрано верно.

2.3. Эквивалентные преобразования для сопротивлений

Последовательное соединение сопротивлений (резисторов) R₁ – R_n (см. рис. 2.9) можно заменить эквивалентным сопротивлением R_экв, равным сумме указанных сопротивлений.

То есть

. (2.9)

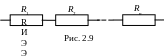
При параллельном сопротивлении резисторов (рис. 2.10) общая проводимость цепи g_экв равна сумме проводимостей

. (2.10)

Соответственно .

Справедливость (2.10) вытекает из того, что ток в сопротивлении R_K

и в соответствии с первым законом Кирхгофа

.

2.4. Мощность и энергия электрических цепей

В общем случае мгновенное значение мощности участка цепи

, (2.11)

где , – мгновенные значения напряжения и тока участка цепи.

Если знаки u и i совпадают, то участок цепи потребляет электрическую энергию (мощность). Если знаки u и i противоположны, то участок цепи отдает (генерирует) электрическую мощность.

При постоянном токе формула мощности

. (2.12)

При протекании тока через активное сопротивление в нем выделяется мощность

. (2.13)

Энергия, выделяющаяся в активном сопротивлении, определяется по закону Джоуля-Ленца

. (2.14)

Для идеального источника ЭДС формулу (2.12) можно записать в виде

. (2.15)

Если направления ЭДС и тока совпадают, то мощность потребляется от источника ЭДС, а если противоположны, то мощность отдается в источник, например, заряжает аккумулятор.