Лабораторная работа № 2 Модели в переменных состояния

В

SISO Design Tools – проектирование систем регулирования с использованием графического интерфейса анализа одномерных линейных (линеаризованных) систем управления

(Single Input/Single Output).

LTI – непрерывная система

(Linear Time Invariation)

MIMO – Multiplay Input/Multiplay Output

пакетах расширения Control System Toolbox системы МАТLАВ приняты следующие способы описания линейных динамических систем с постоянными параметрами: система уравнений первого порядка в фазовом пространстве, или в пространстве состояний системы (ss — state-spase), передаточ­ная функция системы в виде отношения двух полиномов (tf), пе­редаточная функция в так называемом виде нуль/полюс/ коэффи­циент усиления (zpk).

1. Наибольшее распространение получил пер­вый способ, который дает наилучшую точность при вычислениях и в большей степени удобен при теоретических исследованиях и практической реализации алгоритмов управления с применением вычислительных машин и т. д.

При применении этого способа дифференциальные уравне­ния, описывающие динамику системы, имеют вид:

Ax+Bu (2.1)

где х — n-мерный вектор состояния системы (вектор фазовых ко­ординат), u — р-мерный вектор внешних воздействий, состоящий из заданных величин, возмущений, управлений, формируемых ре­гулятором, А и В — переходная матрица системы и матрица управ­лений соответствующих размеров. Предполагается, что измерению доступна только часть состояний системы или их линейных ком­бинаций, такие переменные у называются выходами системы:

у = Сх + Du (2.2)

где у — m-мерный выходной вектор, C, D — матрицы соответст­вующих размеров. Для большинства реальных объектов управле­ния D = 0.

В рассматриваемых пакетах расширения имеется возможность манипулировать с системой, описываемой уравнениями как с одним объектом МАТLАВ. Для этого нужно матрицы А, В, С, B трансформировать в систему, используя команды ss.

2. Передаточная функция (tf) имеет вид

(2.3)

3. ZPK модель имеет вид

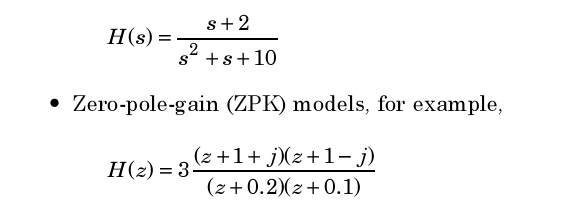(2.4) Далее в качестве примера с использованием метода переменных состояния рассмотрим RCL цепь.

Дана цепь (см. рис. 2.1) Состояние системы характеризуется двумя переменными (x₁,x₂), где x₁ — есть напряжение на конденсаторе u_c(t), и х₂ — ток через индуктивность i_L(t).

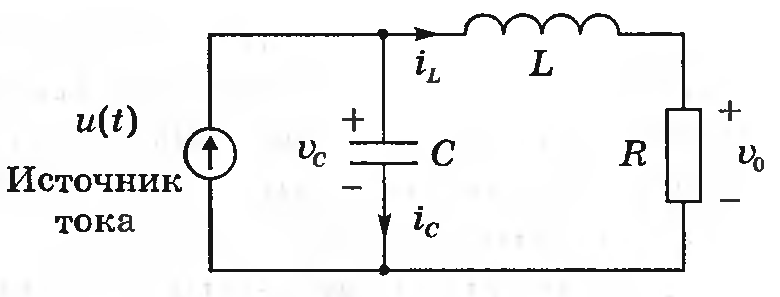
Рис. 2.1

Используя закон Кирхгофа для то­­ков, запишем дифференциальное уравнение, для токов определяющее скорость изменения напряжения на конденсаторе

(2.5)

Следовательно, , где i_L(t) – x₂ , звездочка знак производной. Закон Кирхгофа для напряжений, примененный к правому контуру, дает уравнение, опре­деляющее скорость изменения тока через индуктивность:

- , (2.6)

Следовательно, , где - x₁

Выход системы определяется линейным алгебраическим уравнением

(2.7)

Уравнения 5 и 6 можно переписать в виде двух дифференциальных уравнений относительно двух переменных состояния x₁ и х₂.

= - (2.8)

- (2.9)

Тогда выходной сигнал будет равен

(2.10)

Используя уравнения 8 и 9, а так же начальные условия мы можем определить будущее поведение системы и ее выходную величину.

Воспользовавшись уравнениями 8 и 9 запишем уравнение состояния RCL-цепи

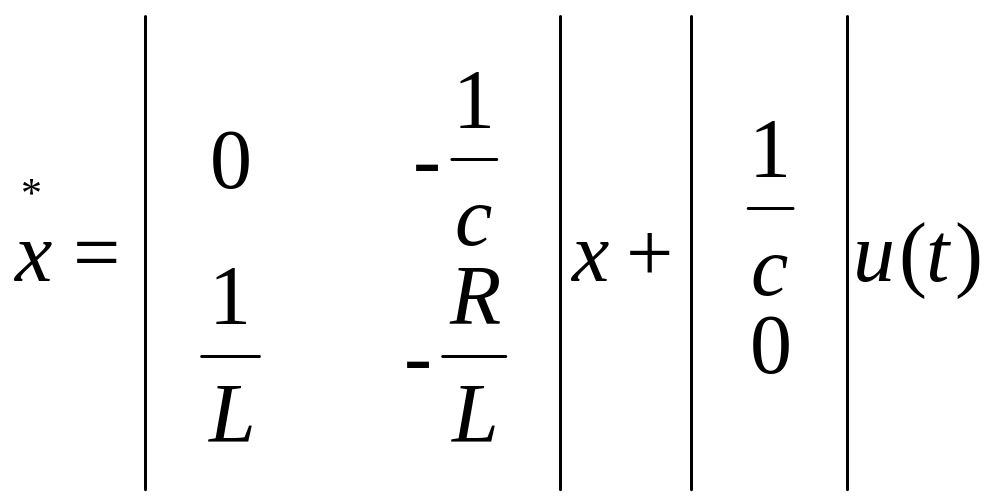(2.11)

Уравнение выхода будет иметь вид:

(2.12)

Если R=3, L=1, C=1/2, то

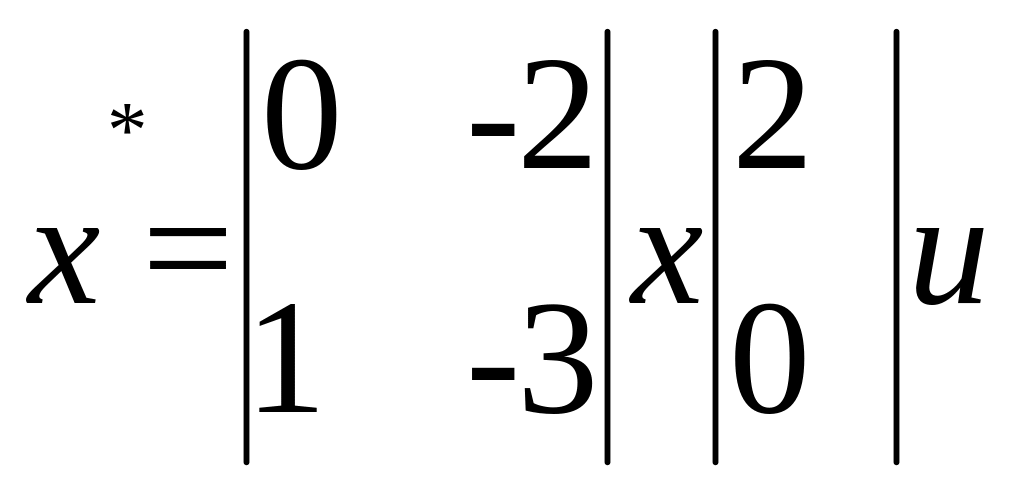и

Теперь создадим систему с использованием команды ss. Создадим m – файл. В командном окне MATLAB последовательно откроем окна File, New, M-file (Script в версии R2010b) и введем текст (комментарии можно не вводить, комментарии начинаются со знака %):^{* ^}

сlear % очистка рабочей области памяти

clc % очистка командного окна

R=3.0 % Ohms

L=1.0 % Henry

C=1/2 % Farad

Далее создадим матрицу A

A = [0 -1/C; 1/L –R/L ]% создание матрицы А

B = [1/C; 0]%создание матрицы B

C = [0 R] % создание матрицы C;

D = [0]

sys_1=ss(A, B, C, D)

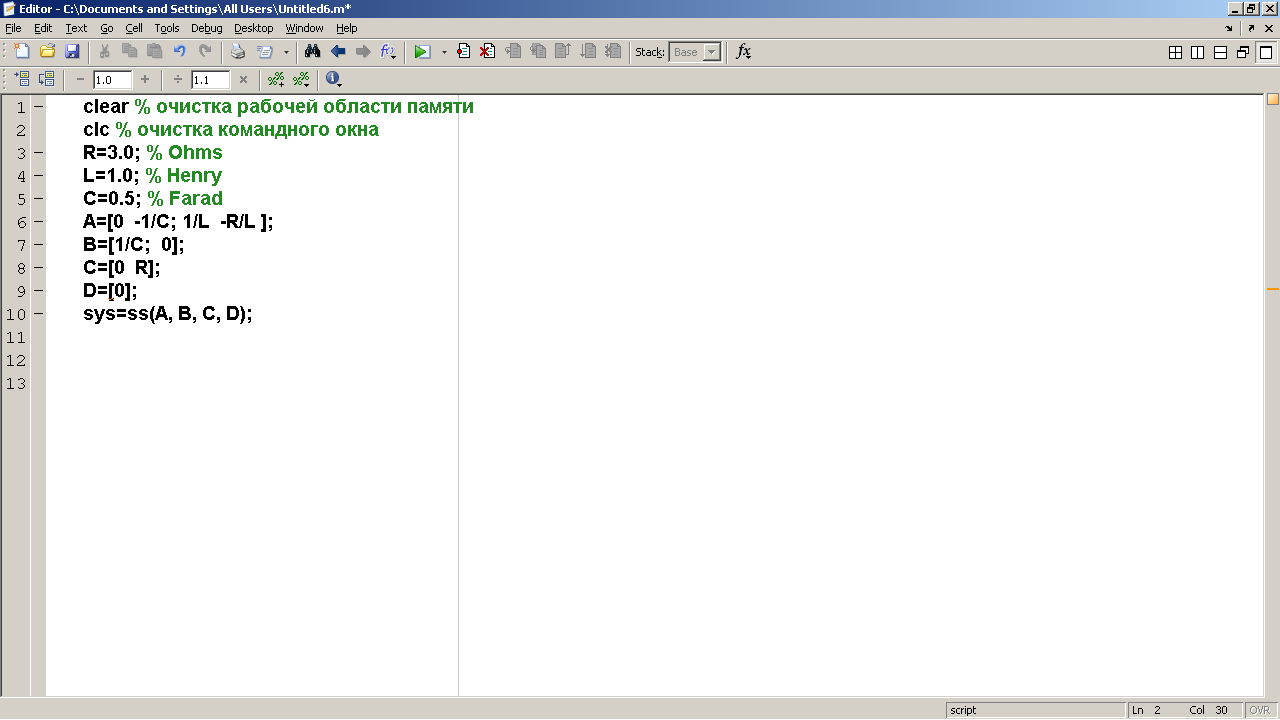
Рис. 2.2

Отметите внимание на следующее: Матрицы можно вводить как одну текстовую строку, причем строки матрицы отделяются друг от друга точкой с запятой, а отдельные элементы строки матрицы разделя­ются пробелами. Если требуемая длина текстовой строки превы­шает ширину страницы, то можно переносить ее на следующую строку, причем в месте разрыва должны

быть поставлены точки, не менее трех. Если после команды имеется точка с запятой, то результаты выполнения команды в командном окне не появляют­ся. Если выполнить эту программу (в окне редактора выполнить Debug и Run или Save and Run), то результат запоминается в рабо­чей области Workplace). Если теперь открыть ее (в окне МАТLАВ выполнить Desktop затем Workplace), то появится содержание ра­бочей области с одним среди прочих объектом sys. Рекомендуем сохранять М-файл:С:\Documents and Setting.

Рис. 2.3

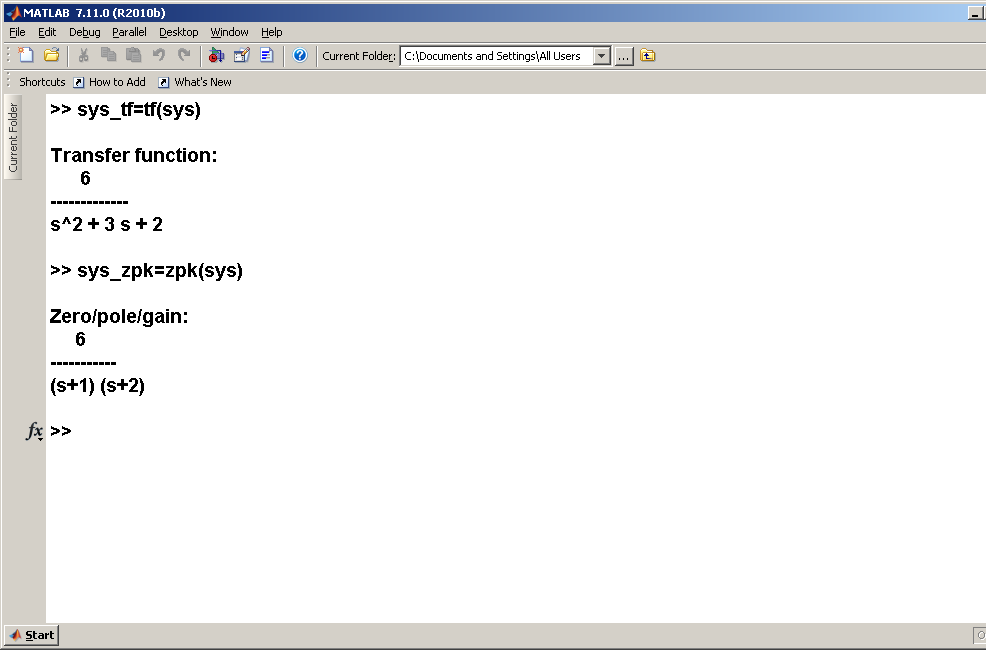
Рис. 2.4

Итак, посмотрим результат работы нашего примера, а именно расчет элементов матриц A, B, C и D и с использованием созданного нами М-файла. Закроем и вновь откроем Matlab. Получим такую картину

Для закрытия Editor:

File-Close Editor.

Напомним, как вводится традиционная передаточная функция в виде отношения полиномов.

Задана передаточная функция САУ:

.

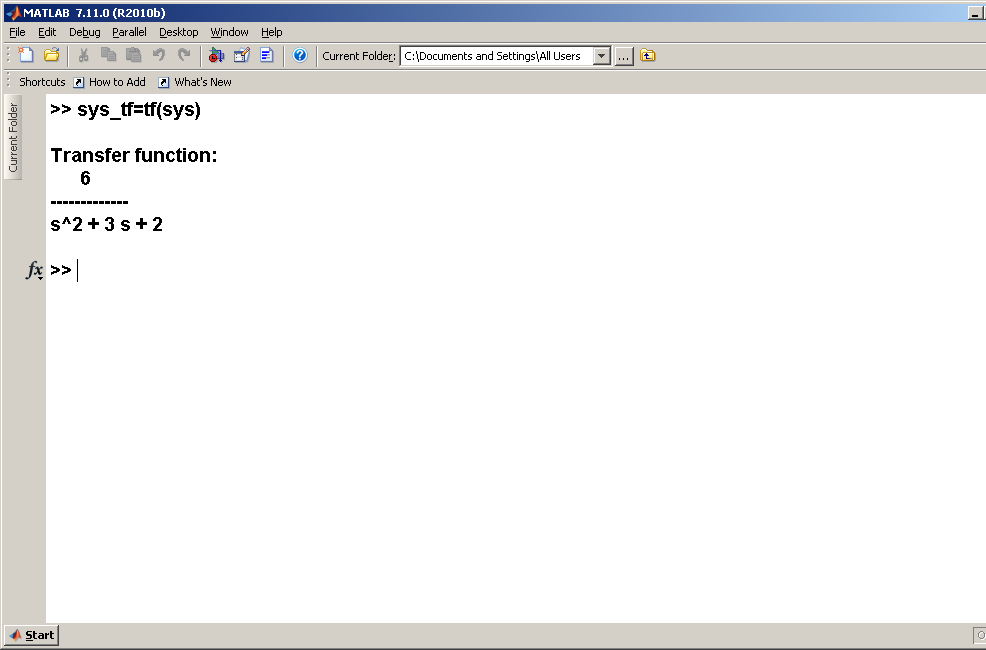
Рис. 2.5

Создадим LTI-объект с именем w, для этого выполним:

Выполним конвертацию LTI- объекта заданного в переменных состояния с использованием команды

>>sys_tf=tf(sys)

Так же выполним конвертацию ZPK- функции из моделей в переменных состояния >>sys_zpk=zpk(sys).

На рис. 2.6 показана схема преобразования двух видов: функция ss позволяет перейти к передаточной к представлению в пространстве состояний, функция tf выполняет обратную задачу. Смысл этих функций представлен на рис. 2.6.

Рассмотрим альтернативные варианты задания и преобразований передаточной функции в переменные состояния.

Например, имеется система третьего порядка

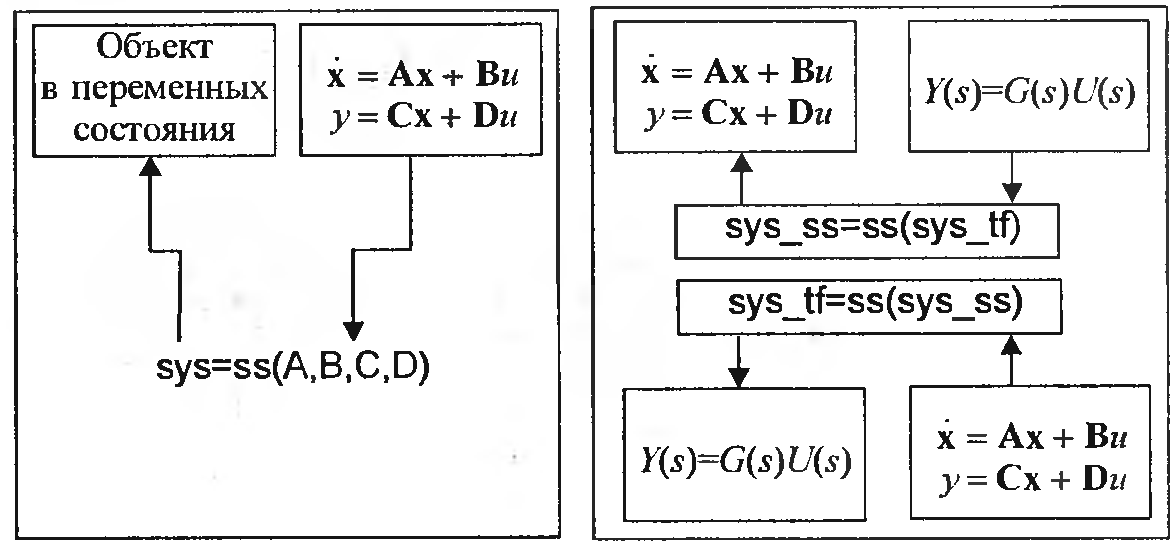
Рис. 2.6

На рис. 2.7 показано, как с помощью функции ss происходит переход от передаточной функции к описанию системы управления Ax+Bu и у = Сх + Du, где

А= , B= , C=[1 0,5 0,375] D=[0] .

Обратите внимание на альтернативное задание числителя (num) и знаменателя (den).

На основе функций представленных в таблице:

1. Постройте графики данного примера (например, step(sys))

2. Постарайтесь сделать тоже самое с использованием LTI-viewer

Рис. 2.7

Синтаксис	Описание
pole(<LTI-объект>)	Вычисление полюсов передаточной функции
zero(<LTI-объект>)	Вычисление нулей передаточной функции
step(<LTI-объект>)	Построение графика переходного процесса
impulse(<LTI-объект>)	Построение графика импульсной переходной функции
bode(<LTI-объект>)	Построение логарифмических частотных характеристик диаграммы Боде
nyquist(<LTI-объект>)	Построение частотного годографа Найквиста