2.3. Вычисление двойного интеграла в декартовых координатах

Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.

Пусть требуется вычислить двойной интеграл , где функция f(x; у) ≥ 0 непрерывна в области D.

Двойной интеграл численно равен объему цилиндроида, ограниченного сверху поверхностью z = f(x;y). Ранее было показано (метод параллельных сечений), что объем тела с известной зависимостью площади поперечного сечения от координаты секущей плоскости равен

,

где S(x) - площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b - уравнения плоскостей, ограничивающих данное тело.

Предполагается, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b, и кривыми у = φ₁(x) и у = φ₂(x), причем функции φ₁(x) и φ₂(x) таковы, что φ₁(x) ≤ φ₂(x) для всех х [а;b] (рис. 6). Такая область называется правильной в направлении оси Оу. Область D называется правильной в направлении оси Оу, если любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.

Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох: х = const, где х [а; b].

В сечении получим криволинейную трапецию ABCD, ограниченную линиями z = f(x;y), где х = const, z = 0, y = φ₁(x) и y = φ₂(x) ( Рис. 7).

Площадь S(x) этой трапеции находим с помощью определенного интеграла

.

Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:

.

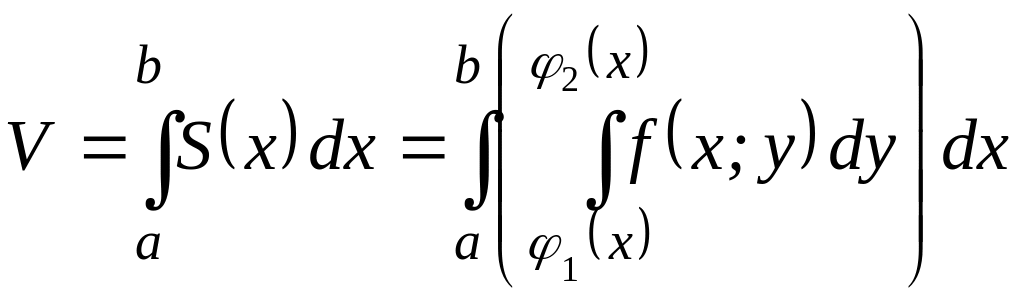Следовательно,

.

Правая часть формулы называется двукратным или повторным интегралом от функции f(x;y) по области D. Двукратный интеграл представляет собой способ вычисления двойного интеграла в декартовых координатах.

Для вычисления двукратного интеграла сначала берется внутренний интеграл . При вычислении внутреннего интеграла по y переменная внешнего интегрирования х считается постоянной. Потом берется внешний интеграл, при этом результат внутреннего интегрирования интегрируем по x; в пределах от а до b.

Если область D является правильной относительно оси Ох, то границы области при этом описываются уже другим образом: область D ограничена прямыми у = с и у = d (с<d), кривыми х = ψ₁(y) и х = ψ₂(y). Двойной интеграл приводится к двукратному интегралу, в котором внешнее интегрирование производится по переменной y, а внутреннее интегрирование _ по переменной x

.

Очень часто область D может быть рассмотрена как правильная в обоих направлениях, и двойной интеграл можно вычислять как по формуле (1.1), так и по формуле (1.2).

Пример 16. Вычислить , где область D ограничена линиями у = x², у = 0, х+ у – 2 = 0.

Решение: На рис. 8 изображена область интегрирования D, которая в данном примере рассматривается как правильная в направлении оси Ох. Это соответствует определенному, удобному в данном примере способу описания границ области D:

Для вычисления данного двойного интеграла воспользуемся формулой (1.2):