2. Двойной интеграл

2.1. Основные понятия и определения

Рассмотрим задачу о нахождении объема тела, ограниченного сверху поверхностью z = f(x;y) (f(x; у) ≥ 0), снизу - замкнутой областью D плоскости хОу, а также боковой цилиндрической поверхностью, имеющей параллельную оси Oz образующую и границу области D в качестве направляющей. Такое тело называется цилиндроидом (рис. 4).

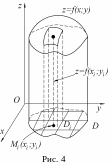
Разобьем область D произвольным образом на п частей, площади которых равны ΔS_i (i = 1,п). Внутри каждой i- той части выберем произвольную точку Mi(x_i; y_i) и посчитаем значение функции z_i = f(x_i;y_i) в этой точке. Рассмотрим совокупность прямых цилиндрических столбиков с площадями оснований ΔS_i и высотой z_i = f(x_i;y_i). Обозначим объем столбика с основанием ΔS_i и высотой z_i = f(x_i;y_i) через ΔV_i. Объем цилиндроида будет приближенно равен сумме всех ΔV_i

.

Сумма

f(x₁;y₁)∆S₁+ f(x₂;y₂)∆S₂+...+f(x_n;y_n)∆S_n= ∆S_i

называется интегральной суммой функции f(x;y) в области D.

Интегральная сумма оказывается тем ближе к объему тела V, чем больше число п и чем меньше размеры «элементарных областей» D_i.

Рассмотрим предел интегральной суммы, когда п стремится к бесконечности таким образом, что наибольший диаметр площадок ΔS_i стремится к нулю. Данный вариант разбиения области D на п частей называется равномерным измельчением. Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается

.

Функция f(x;y) называется интегрируемой в области D; D - область интегрирования, х и у -переменные интегрирования; dx dy (или dS) – дифференциал площади.

Величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела

.

Таким образом, двойной интеграл определяется равенством

.

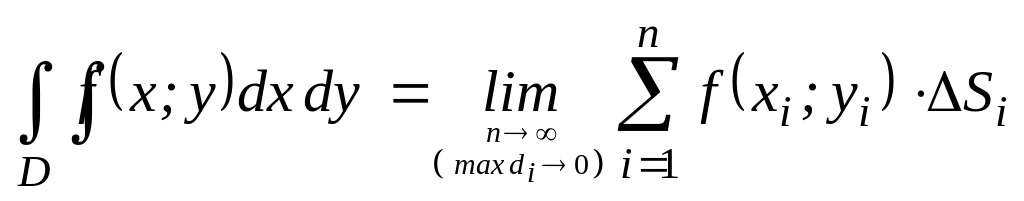Можно показать, что для любой непрерывной функции f(x; у) существует предел интегральной суммы, а, следовательно, определен двойной интеграл.

Стоит отметить, что двойной интеграл может существовать не только для непрерывных функций.

2.2. Основные свойства двойного интеграла

1. Постоянный множитель можно выносить за знак двойного интеграла:

, c - const.

2. Двойной интеграл от алгебраической суммы функций равен сумме двойных интегралов от этих функций:

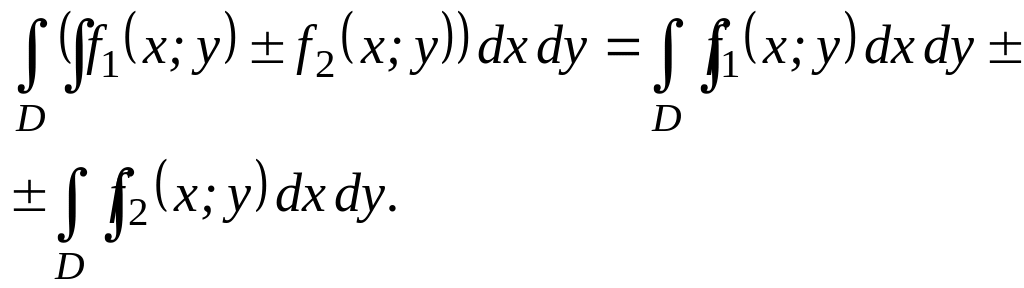
3. Если область D представить в виде суммы областей D₁ и D_2, не имеющих общих внутренних точек (Рис 5.), то

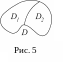
4. Если в области D функции f(x;y) и φ(x;y) удовлетворяют неравенству f(x;y) ≥ φ(x;y), то и двойные интегралы от этих функций подчиняются аналогичному неравенству

.

5. Если функция f(x; y) непрерывна в замкнутой области D, площадь которой равна S, то

,

где m и М - соответственно наименьшее и наибольшее значения подынтегральной функции в области D.

6. (Теорема о среднем) Если функция f(x; y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка (х₀; у₀), что

.