1.5. Применение полного дифференциала в приближенных вычислениях первого порядка

В приближенных вычислениях полное приращение функции f(x,у) заменяют полным дифференциалом: zdz. Предполагается, что слагаемыми x+y, дающими нелинейный по x и y вклад в полное приращение функции, можно пренебречь. Для функции двух переменных вычисления связаны с приближенной формулой:

f(x₀+x, у₀+у)  f(x₀,у₀)+ х+ y.

Пример 5. Вычислить 1,97 .

Решение: Рассмотрим функцию двух переменных f(x,у)=х . В качестве исходной точки возьмем точку М₀(2,0). Надо найти значение данной функции в точке М₁ (1,97; 0,2).

Воспользуемся приближенной формулой

f(x₀+x, у₀+у)  f(x₀,у₀)+ х+ y.

Здесь х₀=2, у₀=0, х=-0,03, у=0,2 , = = =1; = =2, f(x₀,у₀)= f(2,0)=2 2.

Тогда : 1,97 =f(1,97; 0,2)  2+1(-0,03)+20,2 = 2,37.

1.6. Частные производные сложной функции. Полная производная

Пусть дана дифференцируемая функция z=f(u,v), где u и v тоже дифференцируемые функции двух переменных x и у:

u (x, у) и v (x, у). Тогда функция z является сложной функцией двух переменных x и у z = f(u(x,у), v(x,у)).

Найдем = . Дадим переменной х приращение х, зафиксировав значение у. При этом промежуточные аргументы u и v получат частные приращения по х:

_хu= u(x+x,у) - u(x,у) и _хv= v(x+x,у) - v(x,у).

Тогда промежуточные аргументы представляются в виде

u(x+x,у)=u(x,у)+_хu и v(x+x,у)=v(x,у)+_хv.

Функция z=f(u,v) получит полное приращение z:

z=f[u(x+x,у);v(x+x,у)]-f[u(x,у),v(x,у)]= f(u+_xu,v+_xv)-f(u;v).

Поскольку функция z дифференцируема, то ее полное приращение представимо в виде:

z= _xu+ _xv+_xu+_xv,

где выражение _xu+_xv является бесконечно малой величиной более высокого порядка малости по сравнению с _xu и _xv.

Рассмотрим предел отношения :

=

При х 0  и  . Поскольку выражение _xu+_xv является бесконечно малой величиной более высокого порядка малости по сравнению с _xu и _xv, то предел отношения равен

= = .

По аналогии, давая приращение переменной у, и фиксируя переменную х, можно получить выражение для :

= .

Пример 6. Найти частные производные , функции , где , .

Решение:

= = ,

= = .

Если сложная функция зависит от нескольких промежуточных функций, которые в свою очередь зависят от одной переменной , т.е. , то получим

= .

Пример 7. Найти производную , если , а .

Решение:

Воспользуемся формулой = :

=

= .

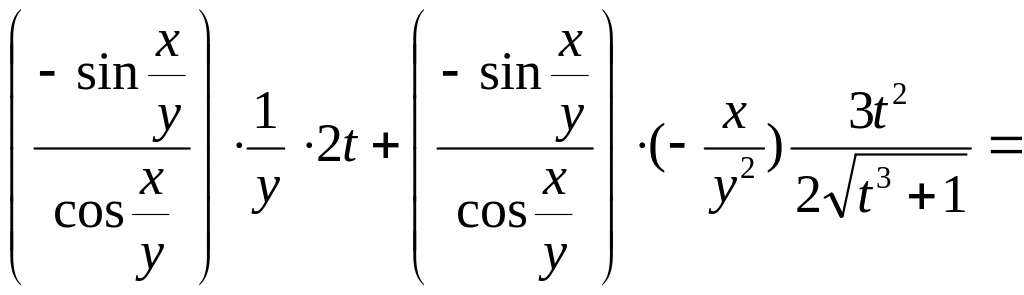
Рассмотрим часто встречающийся в приложениях случай, когда сложная функция зависит от независимой переменной непосредственным образом, а также через промежуточные функции:

где

В этом случае получается формула полной производной:

= .

Пример 8. Найти полную производную , если , а .

Решение:

Поскольку , , , то

= .

Пример 9. Найти полную производную , если , .

Решение:

,

Пользуясь формулой полной производной, получим

=

1.7. Дифференциал сложной функции. Инвариантность формы первого дифференциала

Найдем полный дифференциал сложной функции , если и являются функциями переменных и , т.е. u= u(x, у), v=v(x,у). Имеем :

= .

Раскрыв скобки, и перегруппировав слагаемые, имеем:

= .

Форма записи дифференциала первого порядка не зависит от того, являются ли u и v независимыми переменными или функциями. Это свойство называется инвариантностью формы полного дифференциала.