1.2. Предел и непрерывность функции двух переменных

Определение функции двух переменных требует введение определения  - окрестности точки М. - окрестностью точки M₀ (х₀,у₀) называется внутренняя часть круга радиуса  с центром в точке M₀ (х₀,у₀) или множество точек M (х,у), удовлетворяющих неравенству  .

Число А называется пределом функции двух переменных f(х, у) при х х_0, у у₀ , если для любого сколь угодно малого положительного  найдется такое  > 0, что для всех точек  - окрестности точки М₀(х_0,у₀) выполняется неравенство

< .

Согласно определению, предел А не зависит от способа приближения точки М к точке М_0. В этом случае пишут:

, .

Остаются в силе все теоремы о пределе функции и правила вычисления.

При вычислении предела функции двух переменных вычисляется предел функции f (х, у) по всем возможным прямым, проходящим через точку М₀ (при М М₀), если все эти пределы равны числу А, то .

Пример 1. Найти .

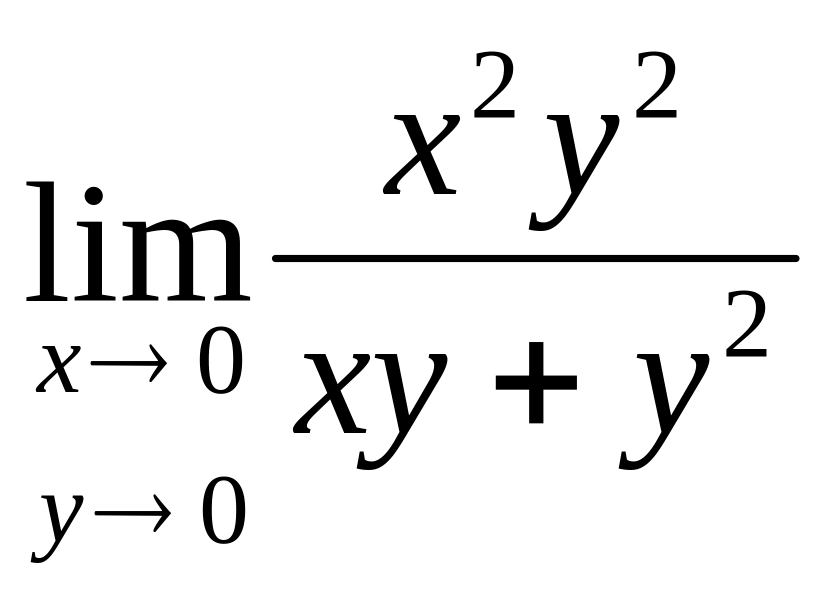Решение: Пусть точка М стремится к точке М₀ по прямой y=kx. Тогда

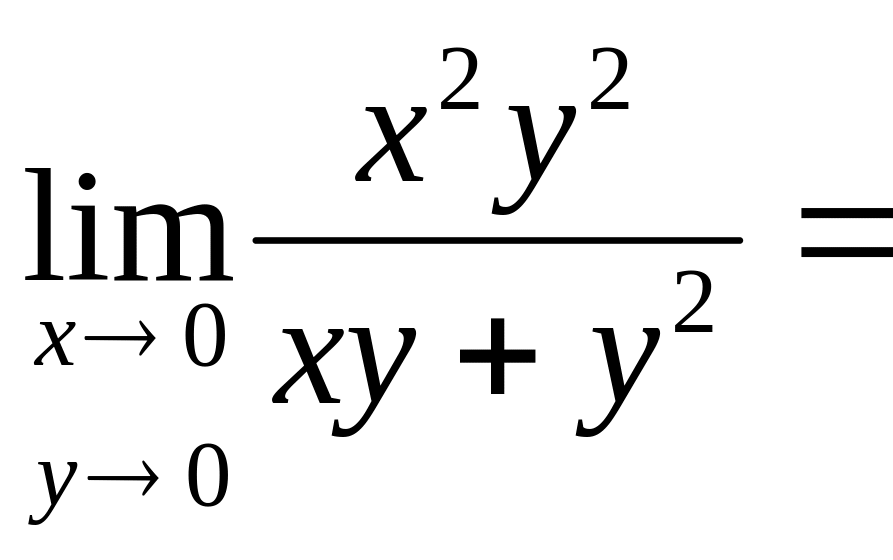
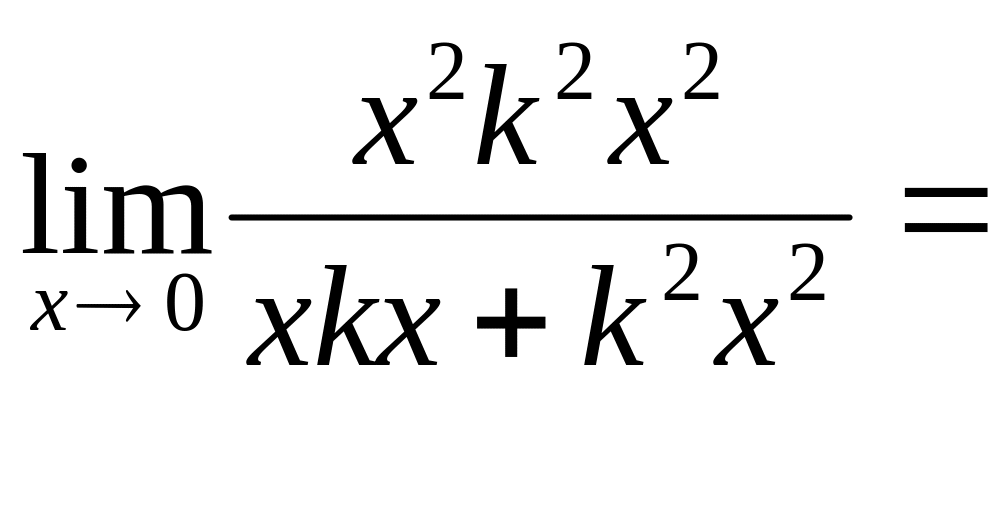
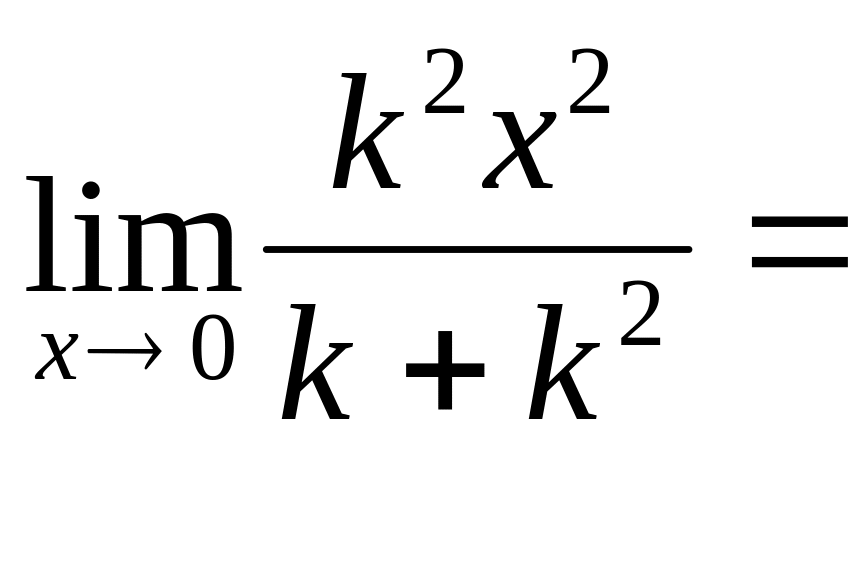0.

Значение предела не зависит от k , поэтому А=0.

Пример 2. Найти .

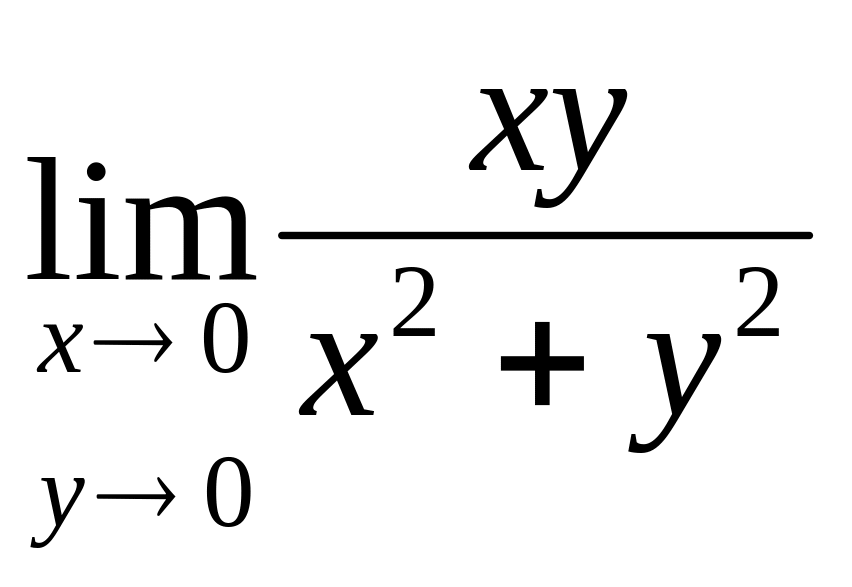Решение:

.

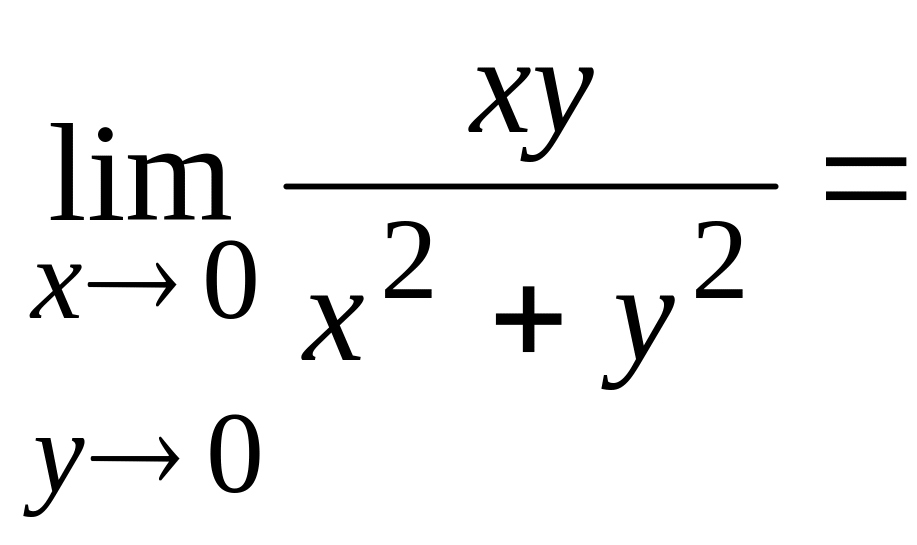
Для различных k получаем различные значения предела, что и означает, что в точке О (0,0) функция предела не имеет.

По аналогии с функцией одной переменной функция f(х,у) называется бесконечно малой, если .

Функция f (х,у) называется непрерывной в точке М₀(х₀,у₀), если .

Для выполнения условия непрерывности необходимо, чтобы:

1) функция f (х, у) была определена в точке М₀(х₀, у₀);

2) существовал предел ;

3) f (М₀) = А.

Функция f (х, у) называется непрерывной в области, если она непрерывна в каждой точке этой области.

Точка М(х,у) называется точкой разрыва функции f(х,у), если функция либо не определена в самой точке, либо не существует предел , либо предел существует, но не равен значению функции в данной точке. Например, функция имеет точку разрыва М₀(0,0).

Определение непрерывности функции нескольких переменных f (x,y) совершенно аналогично определению непрерывности функции одной переменной. Поэтому все свойства, установленные для непрерывных функций одной переменной, остаются в силе для непрерывных функций нескольких переменных:

1.Все элементарные функции нескольких переменных непрерывны в области определения.

2. Если функция f (x,y) непрерывна в замкнутой области , то она ограничена в ней (достигает наибольшего и наименьшего значения).

3. Непрерывная в области D функция, непрерывно переходя от одного своего значения к другому, проходит через каждое промежуточное значение.

Заметим, что непрерывность функции f (х,у) по совокупности аргументов не сводится к непрерывности по каждому аргументу в отдельности. В примере 2 функция по каждому из аргументов в отдельности непрерывна. Например, если М  М₀ по оси Ох (у=0), то z  0 и . Аналогично, при стремлении М  М₀ по оси Оу (х= 0) z  0 и .

1.3. Частные производные и частные дифференциалы первого порядка

Пусть функция z =f (х, у) определена и непрерывна в точке М₀(х₀, у₀) и ее некоторой окрестности. Зафиксируем значение у = у₀, а переменная х пусть испытает приращение х. При этом переместимся из точки в точку . Получим функцию одной переменной z =f (х, у₀). Разность

называется частным приращением функции z по переменной х.

Частной производной функции z по переменной х в точке М₀ (х₀, у₀) называется предел отношения при х0

= = = .

В определении частной производной не все координаты равноправны: переменная у фиксирована, а х изменяется.

При перемещении из точки М₀(х₀,у₀) в точку М₂(х₀,у₀+у) получим частное приращение функции z по переменной

.

Частной производной функции z по переменной в точке М₀ (х₀, у₀) называется предел отношения при 0

= = = = .

Частные производные и характеризуют мгновенную скорость изменения функции z в точке М₀ (х₀, у₀) в направлении координатных осей Ох и Оу.

При вычислении частных производных остаются в силе правила дифференцирования функции одной переменной, а также таблица производных, если другие аргументы считаются постоянными величинами.

Пример 3. Найти частные производные функции .

Решение: = , = Здесь при нахождении переменная считается константой, при нахождении переменная считается константой.

Пример 4. Найти частные производные функции .

Решение:

.

Рассмотрим геометрический смысл частных производных функции двух переменных. Пусть уравнение z =f(х, у) есть уравнение поверхности, изображенной на рис. 2.

Проведем плоскость х= х₀ . В сечении этой плоскостью поверхности получается линия L₂. При данном х₀ рассмотрим на плоскости точку М₀. На поверхности ей соответствует точка Р. Частная производная равна тангенсу угла, образованного касательной к кривой L₂ в точке М с положительным направлением оси Оу:

.

Для уточнения стоит отметить, что касательная лежит в плоскости х= х₀

По аналогии частная производная численно равна тангенсу угла наклона касательной к линии , представляющей сечение поверхности плоскостью у=у₀, т.е. .