Клеман-Дезорм

Министерство науки и высшего образования

Российской Федерации

Федеральное государственное бюджетное образовательное

Учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра физики

ОТЧЕТ

Лабораторная работа по курсу общей физики

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА

Проверил Выполнили

Преподаватель Студенты гр. 120-1

___________ Палешева Е.В. ___________ Бормотов Е.Д.

___________ Дашеев Ц.А.

Томск 2020

ВВЕДЕНИЕ

Целью работы является изучение адиабатического и изохорического процессов в газах, определение отношения теплоемкостей (коэффициента Пуассона) и числа степеней свободы.

1 ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКИ ИЗМЕРЕНИЙ

В

Водяной

манометр

качестве экспериментальной установки используется прибор Клемана-Дезорма, с помощью которого можно определить коэффициент Пуассона. Схема прибора представлена на рисунке 1.1.

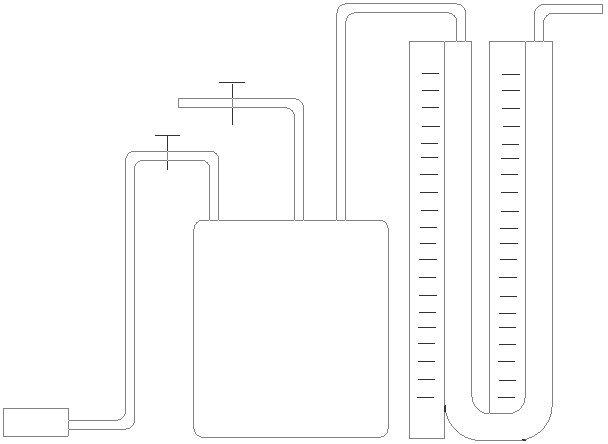
Баллон

Насос

Клапан

Зажим

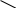
Подводящая

трубка

Рисунок 1.1 – Схема экспериментальной установки.

При проведении процесса, изображенного на рисунке 1.2, измерялись значения 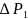и .

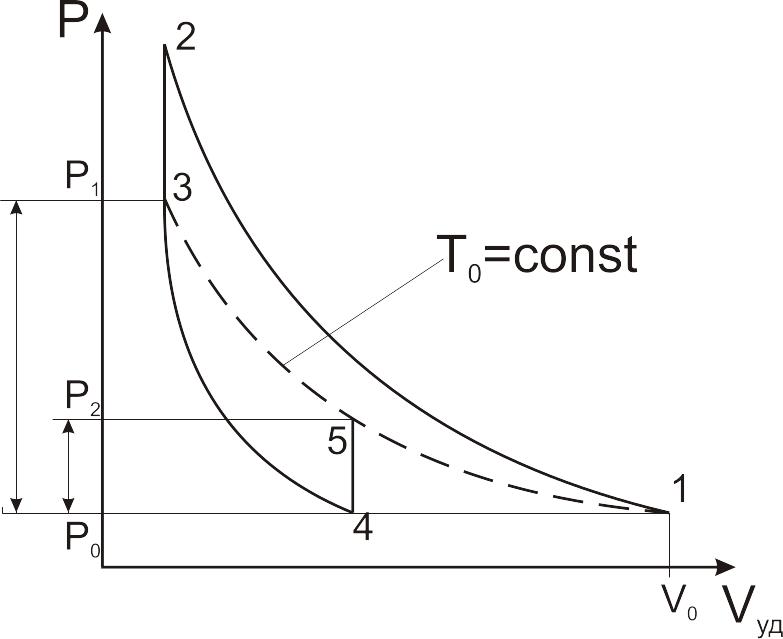
Рисунок 1.2 – PV_уд-диаграмма процессов в газе.

2 ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Коэффициент Пуассона (отношение молярных теплоемкостей газа C_v и Cp при постоянном давлении и при постоянном объеме соответственно):

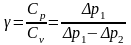. (2.1)

Погрешность прямых измерений разности давлений составляет:

(<p_1,2>) = 5 мм. (2.2)

Относительная погрешность измерения <p_1,2>:

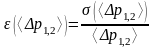. (2.3)

Абсолютная погрешность косвенного измерения (<p₁>-<p₂>):

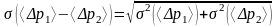. (2.4)

Относительная погрешность измерения (<p₁>-<p₂>):

. (2.5)

Относительная погрешность косвенного измерения <>:

. (2.6)

Случайная погрешность измерения <>:

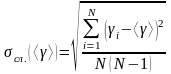, (2.7)

где N – число опытов.

Систематическая погрешность измерения <>:

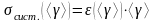. (2.8)

Суммарная абсолютная погрешность измерения <>:

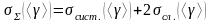. (2.9)

Суммарная относительная погрешность измерения <>:

. (2.10)

Среднее число степеней свободы молекулы газа:

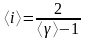. (2.11)

Абсолютная погрешность косвенного измерения <i>:

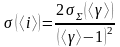. (2.12)

Относительная погрешность измерения <i>:

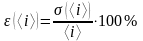. (2.13)

3 РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ

Результаты прямых и косвенных измерений представлены в таблице 3.1.

Таблица 3.1 – Результаты прямых и косвенных измерений

Опыт	p1, мм	p2, мм	(p1-p2), мм	
1	230	70	160	1,44
2	230	70	160	1,44
3	210	50	160	1,31
4	210	50	160	1,31
5	190	50	140	1,357
6	230	70	160	1,44
7	200	60	140	1,42
8	200	50	150	1,33
9	240	50	190	1,26
Ср. знач.	215,5	57,7	157,7	1,367

Значения , внесенные в таблицу, рассчитаны по формуле (2.1):

.

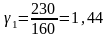Аналогично рассчитаны значения  остальных опытов.

Относительная погрешность измерения <p_1,2> по формуле (2.3), используя значение погрешности полученной в формуле (2.2):

.

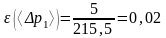Аналогично :

.

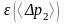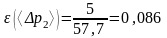Абсолютную погрешность косвенного измерения (<p₁>-<p₂>) по формуле (2.4):

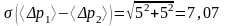(мм).

Относительная погрешность измерения (<p₁>-<p₂>) по формуле (2.5):

.

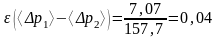Относительная погрешность косвенного измерения <> по формуле (2.6):

.

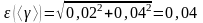Случайная погрешность измерения <> по формуле (2.7):

.

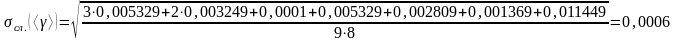Систематическая погрешность измерения <> по формуле (2.8) равна:

.

Суммарную абсолютную погрешность измерения <> рассчитывается по формуле (2.9):

.

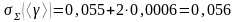Оценка качества измерений коэффициента Пуассона.

По формуле (2.10) рассчитывается суммарная относительная погрешность измерения <>:

.

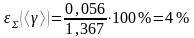Среднее число степеней свободы молекулы газа находится по формуле (2.11):

.

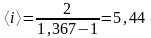Расчёт абсолютной и относительной погрешности измерения <i> произведён по формулам (2.12) и (2.13) соответственно:

.

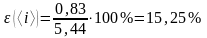ЗАКЛЮЧЕНИЕ

В результате проделанной работы были рассчитаны среднее значение коэффициента Пуассона для воздуха и среднее число степеней свободы газа:

<> = 1,367 ± 0,054;

= 4 %;

<i> = 5,44 ± 0,83;

= 15,25 %.

При изучении адиабатического и изохорического процессов в газах на примере определения отношения теплоемкостей газа, доказана справедливость формулы нахождения коэффициента Пуассона: .
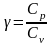