Изучение свойств диэлектриков в поле плоского конденсатора
.docxМинистерство науки и высшего образования
Российской Федерации
Федеральное государственное бюджетное образовательное
Учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики
ОТЧЕТ
Лабораторная работа по курсу общей физики
Изучение свойств диэлектриков в поле плоского конденсатора
Проверил. Выполнил
Преподаватель Студент гр. 120-1
___________ Палешева Е.В. ___________ Бормотов Е.Д.
Томск 2020
ВВЕДЕНИЕ
Целью данной работы является определение величины относительной диэлектрической проницаемости и нормальной составляющей вектора поляризации для различных диэлектриков, помещённых в электрическое поле плоского конденсатора.
1 ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ
Схема экспериментальной установки представлена на рисунке 1.1.
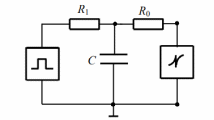
Рисунок 1.1 – Схема установки.
Метод измерения основан на исследовании временной зависимости напряжения на конденсаторе при его заряде или разряде через сопротивление электрической схемы.
2 ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Внутренне сопротивление генератора находится по формуле:
,
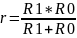(2.1)
Где R1 = 1.3 МOм;
R0 = 1.3 МOм;
Емкость конденсатора рассчитывается по формуле:
,
(2.2)
Где r – внутренне сопротивление генератора;
a – угловой коэффициент прямой равный 5.297;
Относительную диэлектрическую проницаемость рассчитывается по формуле:
,
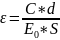(2.3)
Где C – емкость конденсатора;
d – толщина диэлектрика;
E0 – электрическая постоянная равная 8.85*10^(-12);
S – площадь электрода;
Поверхностная площадь заряда выражается по формуле:
,
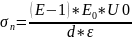(2.4)
Где Uo – начальное напряжение;
Электрический момент вычисляется по формуле:
(2.5)
Модуль вектора поляризации:
P=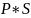
(2.6)
Относительная погрешность C вычисляется по формуле:
,
(2.7)
Где
– относительная погрешность времени;
-
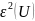относительная погрешность напряжения;
Относительная погрешность расстояния между пластинами рассчитывается по формуле:
,
(2.8)
Где
- абсолютная погрешность расстояния
между пластинами;
Относительная погрешность относительной диэлектрической проницаемости выражается по формуле:
,
(2.9)
Где
- относительная погрешность площади
электрода;
Абсолютная погрешность косвенного измерения емкости конденсатора:
.
(2.10)
Абсолютная погрешность косвенного измерения относительной диэлектрической проницаемости вычислим по формуле:
(2.11)
3 РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ
Все вычисления заносим в таблицу 3.1
Таблица 3.1 – Результаты измерений.
-
№
Диэлектрик, толщина 1,6 мм
Примечания
t, мс
U, В
Ln(U0/U)
1
0.116
0.924
0
ε(U)=5%
ε(t)=5%
σ(d)=0,01мм
S=100см2
ε(S)=5%
U0=0.924 B
2
0.258
0.398
0.842
3
0.357
0.227
1.404
4
0.448
0.142
1.873
5
0.531
0.0884
2.347
6
0.602
0,067
2.624
7
0.652
0,0492
2.933
8
0.694
0,042
3.091
9
0.723
0,0386
3.175
10
0.751
0,0278
3.504
Построим
линеаризованный график зависимости
Ln(U0/U)
от t: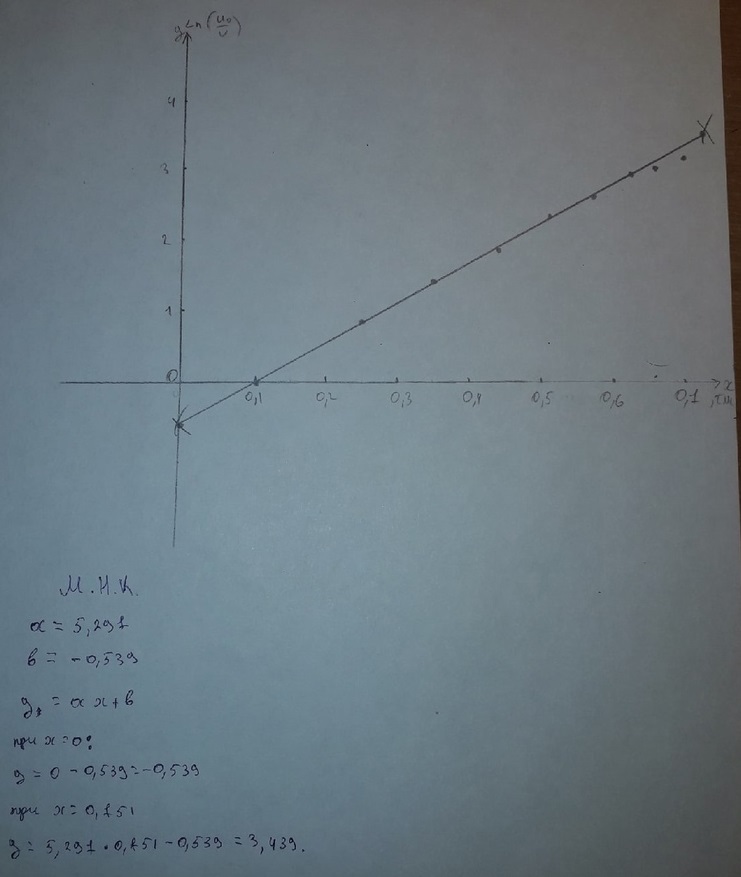
По формуле 2.1 рассчитаем внутреннее сопротивление генератора:
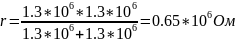
По формуле 2.2 найдем емкость конденсатора:
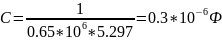
По формуле 2.3 вычислим относительную диэлектрическую проницаемость:
По формуле 2.4 рассчитаем поверхностную плотность заряда:
По формулам 2.5 и получим 2.6
То есть поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации в данной точке диэлектрика.
По формуле 2.7 вычислим относительную погрешность C:
Найдем относительную погрешность расстояния между пластинами по формуле 2.8:
По формуле 2.9 вычислим относительную погрешность диэлектрической проницаемости:
Абсолютная погрешность косвенного измерения емкости конденсатора вычисляется по формуле 2.10:
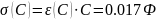
Абсолютная погрешность косвенного измерения относительной диэлектрической проницаемости вычислим по формуле 2.11:
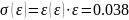
Заключение
С учетом погрешностей вычислили:
C
=
Ф
=
=
