
Макроекономіка Радіонова
.pdf
Розділ 2. ЗАГАЛЬНА ЕКОНОМІЧНА НЕРІВНОВАГА
2.1. Нерівновага як узгодження ринків без узгодження цін. Модель нерівноваги Барро—Гросмана
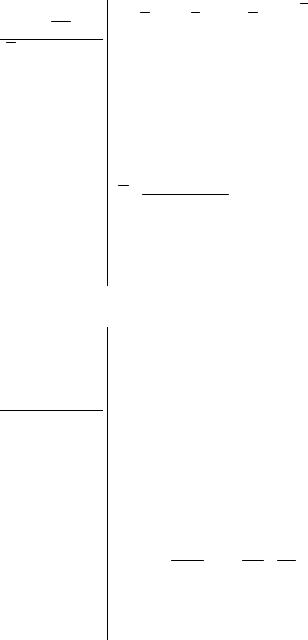
1 Графічно ситуація може бути ілюстрована так:
Ринок праці |
|
Ринок товарів |
Ринок облігацій |
||
W/P |
S |
P |
Y S |
r |
B1D B2D |
|
L1 |
LS |
|
|
|
|
|
2 |
|
|
|
W*/P |
|
P* |
Y D |
r* |
|
|
LD |
|
Y1D2 |
|
BS |
LD |
LS L |
|
Y S YD Y |
BD |
BS B |
Система графіків ілюструє те, що надлишок пропозиції ринку праці узгоджується з надлишками попиту на товарному ринку та ринку запозичень, отже, рівняння матиме вигляд:
WP (LS − LD ) = (Y D −Y S )+ (BD − BS ) .
2 Умова
M1 = 10
M 2 = 15
V = 12,8
LS = 2W
Y = 32L1/ 2
(LS − LD ) - ?
Розв’язання
Визначаємо (LS − LD ) як різницю між пропозиці-
єю праці після збільшення кількості грошей в обігу й виникнення «грошової ілюзії» найманих працівників та зайнятістю в умовах рівноваги до грошового «збурення».
Рівноважний обсяг зайнятості знаходимо з виробничої функції та функції пропозиції праці, оцінивши заробітну плату з позицій підприємців та заробітну плату з позицій найманих праців-
ників:
заробітна плата з позицій підприємців (зарплата попиту) визначаєтьсяза ринковим правилом
MPL =W D = |
∂Y |
|
∂Y |
= |
32 |
= |
16 |
; |
|
∂L |
|
∂L |
|
2 L |
|
L |
|
зарплата з позицій найманих працівників (зарплата пропозиції) визначається з рівняння про-
позиції праці: W S = L2 .
371

З рівності 16L = L2 L = 4 .
Реальний продукт за рівноважної зайнятості ста-
новитиме: Y = 32 4 = 64.
4 = 64.
З рівняння M ×V = P ×Y знаходимо рівень цін до збільшення пропозиції грошей: P = 10×6412,8 = 2 .
Визначаємо, яким буде номінальний продукт (дохід) після грошового «збурення»:
Y = 15×12,8 =81. 2
Розраховуємо пропозицію праці, зважаючи на те що наймані працівники сприйняли зростання номінальних доходів як реальне, скориставшись виробничою функцією
Y = 32L1/ 2 : 81 = 32×L1/ 2 L1/ 2 = 2,53 L = 6,4 .
Знаходимо показник перевищення пропозиції праці над попитом: (LS − LD ) = 6,4 – 4 = 2,4.
Відповідь: надлишок пропозиції на ринку праці становитиме 2,4 одиниці.
3Ситуації відповідатиме така система рівнянь:
W *(LD − LS1) =Y S −Y D1 ;
LS1 = LS1 W , |
M |
,Pr,Y |
; |
|
|
|
P |
|
|
|
|
Y D1 =Y D1 Pr+W × LD1 |
, |
M |
. |
||
|
|
|
|
P |
|
Характерними ознаками ситуації одночасного існування надлишку попиту на працю та надлишку пропозиції товарів є:
•домінування домашніх господарств на обох ринках;
•занижені ціни товарного ринку.
4 Умова |
|
Розв’язання |
|
P = 4,5 |
|
Ефективний попит домашніх господарств вини- |
|
W =1,5 |
|
кає внаслідок раціонування на ринку праці. |
|
LS =18 − |
5W |
2 |
Оскільки в задачі не дана функція споживання, |
|
то її треба вивести з бюджетного обмеження та |
||
Pврахувати в ній факт раціонування на ринку праці:
372
Pr = 0,3 P2
W
С — ?
5 Умова
Y = L1/ 2
U =C1/ 2(14−L)1/ 2
P×C =W ×L +Pr
W =1
P = 5
LS = LD — ?
LS , LD — ?
P ×C = W × L + Pr C = W × L + Pr . P
Визначаємо пропозицію праці та прибуток з урахуванням цін, що встановилися на товарному ринку та ринку праці:
S |
|
5×1,52 |
=15,5 ; Pr = 0,3× |
4,52 |
= 4,05 . |
L |
=18 − |
|
|
||
4,5 |
1,5 |
Підставляємо у формулу споживання значення пропозиції праці та прибутку, що враховують фактичні ціни двох ринків:
С = 1,5×15,5 + 4,05 = 6,1 . 4,5
Відповідь: споживання на рівні 6,1 одиниці є ефективним, остільки воно визначено з урахуванням раціонування (обмеження) домашніх господарств на ринку праці.
Розв’язання
Гіпотетичне (таке, що відповідає рівновазі за Вальрасом) значення пропозиції праці та споживання визначається в результаті максимізації за функцією Лагранжа:
Φ = C1/ 2 (14 − L)1/ 2 – λ(P ×C −W × L − Pr) .
Дістаємо систему з двох рівнянь:
∂Φ |
= |
1 |
|
(14 − L)1/ 2 |
= λP ; |
|
∂C |
2 |
|
C1/ 2 |
|||
|
|
|
||||
∂Φ |
= |
1 |
|
C1/ 2 |
= λW . |
|
∂L |
2 |
|
1/ 2 |
|||
|
|
(14 − L) |
|
|||
Розв’язавши обидва рівняння за λ та прирівнявши їх, маємо вирази:
LS =14 − PW×C ; C = 7PW + 2PrP .
Основні параметри діяльності фірм — попит на працю та максимальний прибуток — визначаємо виходячи з виробничої функції та правила формування реальної зарплати:
373

1
W |
= |
∂Y |
= |
2 |
LD = |
P2 |
|
. |
P |
∂L |
1/ 2 |
4W |
2 |
||||
|
|
L |
|
|
||||
Пропозиція фірм виходячи з попиту на ринку праці визначатиметься так:
Y |
S |
|
P2 |
|
1/ 2 |
P |
. |
|
|
= |
|
|
|
= |
|
||
|
4W |
2 |
2W |
|||||
|
|
|
|
|
|
|
||
Знаходимо гіпотетичний прибуток фірм:
D |
|
P |
|
P2 |
|
P2 |
. |
|
Pr = P ×Y −W × L |
= P |
|
|
−W |
|
= |
|
|
|
4W 2 |
4W |
||||||
|
|
2W |
|
|
|
|||
Спрощуємо вираз функції споживання та пропозиції праці домашніх господарств з урахуванням виведеного значення прибутку:
|
7W |
|
|
P2 |
|
|
|
7W |
|
|
|
P |
|
|
|
|
|||
C = |
+ |
4W |
|
= |
+ |
|
|
, |
|
|
|||||||||
P |
|
|
|
|
8W |
|
|
||||||||||||
|
|
|
2P |
|
|
|
|
P |
|
|
|
|
|
||||||
|
|
|
|
|
7W |
|
|
|
P |
|
|
|
|
|
|||||
|
|
|
P |
|
|
|
+ |
|
|
|
|
|
|
|
P2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
LS =14 − |
|
P |
|
8W |
= |
7 + |
|
. |
|||||||||||
|
W |
|
|
8W 2 |
|||||||||||||||
Виходячи із суті закону Вальраса про врівноважування системи за рахунок співвідносних цін, знаходимо співвідносні ціни, задавши значення
W =1 . Ураховуємо те, що в рівноважній системі LS = LD . Отже, маємо:
1 P2 |
= 7 + |
P2 |
P = 7,5 при W =1 . |
||
|
|
|
|||
4 W 2 |
8W 2 |
||||
|
|
||||
Знаючи співвідносні рівноважні ціни двох ринків, визначаємо гіпотетичну пропозицію праці:
LS = LD ≈14 .
Підставляємо нерівноважні ціни (W =1 , P = 5 ) у функції попиту та пропозиції:
LS =10,125 , LD = 6,25 — та знаходимо
LS − LD = 3,875 .
Відповідь: при нерівноважних цінах на ринку праці утворюється надлишок пропозиції праці у 3,875 одиниці.
374
2.2. Нерівновага як нестабільність, спричинена фінансовими та грошовими імпульсами.
Моделі Варбуртона—Єгера та Бліндера—Солоу
1 Умова
∆M = 50 dMdC = 0,25
dMdL = 0,15
Y = 0,1L2
Y0S =Y0D
(Y1S −Y1D ) — ?
2 Умова
Y = 9
P =1,2 Pe =1,08
YS =Y +12(P−Pe)
Y = 0,1L2
∆L —?
Розв’язання
За логікою моделі Варбуртона—Єгера за економічного спаду відбувається скорочення споживання та збільшення пропозиції праці. Це і створює розрив між сукупною пропозицією та
попитом (Y1S −Y1D ).
Масштаб скорочення попиту оцінюємо за величиною зменшення споживання, ураховуючи коефі-
цієнтеластичності: −∆Y D = −∆C = 0,25×∆M =12,5 .
Масштаб збільшення пропозиції визначаємо з урахуванням відповідного коефіцієнта еластичності та виробничої функції:
∆L = 0,15×∆M = 7,5 ;
∆Y S = dYdL = 0,2×7,5 =1,5 ;
(Y1S −Y1D ) = | ∆Y D | +∆Y S =12,5 +1,5 =14 .
Відповідь: величина розриву, що виник унаслідок скорочення пропозиції грошей, становить 14 одиниць.
Розв’язання
За логікою моделі Варбуртона—Єгера одним з наслідків неочікуваної зміни пропозиції грошей стає збільшення пропозиції праці:
M unexS ↓→ C ↓, LS ↑→Y D <Y S →Y S ↓.
Пропозиція праці корелює з пропозицією на товарному ринку. До зміни грошової пропозиції пропозиція товарного ринку становила 9 одиниць, оскільки передбачається тотожність фактичних та очікуваних цін.
Після змін пропозиції грошей обсяг товарної пропозиції змінився:
Y S = 9 +12(1,2 −1,08) =10,44 .
Обсяг пропозиції праці, що відповідає товарній пропозиції до змін, за виробничою функцією становив:
375

3 Умова
∆G = 40
B0 = 0
Y0 = 750
G0 =150
M0 =346
K0 =140
Y=0,75(Y +B−T)+
+0,3W+I +G
M= 0,5(0,8Y +
+0,2W −50r)
I=100 −100r T = 0,3(Y − B)
me — ?
L = 9 |
≈ 9,45 . |
|
0 |
0,1 |
|
|
|
|
Новій пропозиції товарного ринку відповідає нова пропозиція праці:
= 10,44 ≈
L1  0,1 10,21;
0,1 10,21;
∆L = L1 − L0 ≈ 0,8 .
Відповідь: пропозиція праці після несподіваного зменшення пропозиції грошей зросла на 0,8 одиниці.
Розв’язання
Умовою перебування економіки у стані рівноваги за моделлю Бліндера—Солоу стійка рівновага при борговому фінансуванні досягається за відсутності витіснення (графік 2 на рис. 2.8), а мультиплікатор витрат є більшим від 1. Натомість нестійка — при витісненні (графік 1 на рис. 2.8), коли мультиплікатор менший за 1. Отже, щоб розв’язати задачу, треба знайти зна-
чення мультиплікатора me = ∆∆GY .
Для цього бракує ∆Y . Його можна визначити як
∆Y =Y1 −Y0 .
Для обчислення Y1 скористаємося функціями з умови задачі:
Y1 = 0,75(Y1 + B1 −T1) +0,3W1 + I1 +G1 .
Для розрахунку B1 необхідно врахувати те, що боргові зобов’язання використані для фінансу-
вання ∆G |
попереднього |
року, отже, ∆G = |
B1 |
. |
|
||||
|
|
|
r |
|
Звідси B1 = ∆G ×r0 . |
|
0 |
|
|
|
|
|
||
Значення |
r0 знаходимо |
з функції пропозиції |
||
грошей M0 = 0,5(0,8Y0 +0,2W0 −50r0 ) , обчисливши обсяг багатства у початковому періоді:
W0 = K0 + M0 + B0 = 500 ;
r0 = 0,16 B1 = 40×0,16 −6,4 .
376
4 Умова
∆C =10
CW dK = 12 ∆C
∆I =15
∆K =10
( IK +CW ) — ?
Нова величина багатства з урахуванням облігацій становитиме: W1 = 506,4 .
Під впливом державних боргових зобов’язань змінюється ставка відсотка, яку знаходимо з рівняння пропозиції грошей при новому значенні
обсягу багатства: r1 = 0,183 .
Обсяг інвестицій за нової ставки відсотка буде таким: I =100 −100 ×0,183 −81,7 .
З урахуванням нових значень змінних після боргового фінансування державних витрат знаходимо продукт:
Y1 = 0,75 [Y1 + 6,4 − 0,3(Y1 − 6,4)]+ 0,3×506,4 + 81,7 + +150 + 40 Y1 = 905 ;
m = |
∆Y |
= |
905 −750 |
= 3,87 . |
|
∆G |
40 |
||||
e |
|
|
Відповідь: оскільки мультиплікатор більший за 1, тоекономіка перебуває устані стійкої рівноваги.
Розв’язання
Умовою перебування економіки у стані рівноваги за моделлю Бліндера—Солоу є дотримання
нерівності IK +CW < 0.
Для визначення IK за формулою IK = − |
dI |
на- |
|
dK |
|||
|
|
||
явні всі необхідні дані з умов задачі. |
|
||
Оскільки CW — показник еластичності |
змін |
||
споживання лише за зміною капіталу, то від загального приросту ∆C =10 беремо лише половину. Отже, dCK = 5 .
Визначаємо показники еластичності:
IK = − dKdI = −1015 = −1,5 ;
CW = dKdC = 105 = 0,5 ;
IK +CW = −1,5 +0,5 = −1 < 0.
Відповідь: економіка перебуває у стані стійкої рівноваги.
377

4 Умова
∆G =8
C = 0,75Y + 5i +
+ 0,25W
I = 50 −15i M D = 0,4Y −
− 20i − 0,4W
M D = M S
∆Y — ?
Розв’язання
Ситуація, що передбачена умовами задачі, зо-
бражена на графіку 2 (рис. 2.9).
Зміна продукту на першому етапі впливу додаткових державних витрат може бути оцінена так:
∆Y = mIS ×∆G .
Для визначення скоригованого з урахуванням взаємодії функцій IS та LM мультиплікатора mIS
треба застосувати формулу mIS |
= |
meh |
. |
|||||||
h + mekb |
||||||||||
Усі змінні для визначення mIS |
|
|
||||||||
беремо з вироб- |
||||||||||
ничих функцій. Отже, |
|
|
|
|||||||
|
|
|
|
1 |
×20 |
|
|
|
|
|
mIS = |
|
1−0,75 |
=1,82 . |
|
|
|
||||
|
|
|
|
|
||||||
20 + |
|
|
1 |
×0,4×15 |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
1 |
−0,75 |
|
|
|
|||||
|
|
|
|
|
|
|
||||
Зміна продукту до фінансування надлишкових бюджетних витрат борговими зобов’язаннями становила ∆Y =8×1,82 =14,56 .
Після фінансування додаткових державних витрат борговими зобов’язаннями починається дія ефекту багатства, що втілюється у прирості споживання. Виходячи з функції споживання
споживчі витрати зростуть так: ∆C = 8×0,25 = 2 . Під впливом збільшення споживання продукт зросте додатково на ∆Y = 2×1,82 = 3,64 .
Дія ефекту багатства одночасно втілюється у зменшенні попиту на гроші. Виходячи з функції
попиту на гроші −∆M =8×0,4 = 3,2 .
Зміна продукту за зміною пропозиції грошей з урахуванням взаємодії функцій IS та LM має оцінюватися з використанням мультиплікатора:
mLM |
= |
meb |
|
; |
|
|
||
|
|
|
|
|
|
|||
|
|
h + mekb |
|
|
||||
|
|
|
|
|
1 |
×15 |
|
|
mLM = |
|
|
1− 0,75 |
=1,36 . |
||||
|
|
|
||||||
20 + |
|
|
1 |
×0,4 ×15 |
||||
|
|
1 |
−0,75 |
|
||||
|
|
|
|
|
||||
378

Отже, зміна продукту під впливом зменшення пропозиції грошей становитиме:
∆Y = −3,2×1,36 = −4,352 .
Загальна зміна продукту, зумовлена фінансовим імпульсом, дорівнюватиме:
∆Y =14,56 +3,64 − 4,352 =13,848 .
Відповідь: з урахуванням дії ефекту багатства фінансовий імпульс втілився узростанні продукту на 13,848 одиниці, що є меншим, ніж початкова зміна продукту в 14,56 одиниці.
Розділ 3. МАКРОЕКОНОМІЧНА ДИНАМІКА
3.1. Економічні коливання. Теорія реального бізнесового циклу та модель Прескотта—Кідленда
1 Умова
Yt* =1,05Yt*−1
Y1 =100
−
A3 = 25 c′ = 0,8
k = 0,6
Y3 −Y3* — ?
Розв’язання
За вихідними даними задачі для визначення відхилення фактичних значень ВВП від трендових необхідно скористатися рівнянням з моделі му-
льтиплікатора-акселератора.
За рівнянням тренду значення ВВП у трьох роках мали б бути такими: Y1* =100 ; Y2* =105 ;
Y3* =110,25 .
Для розрахунку фактичних значень ВВП у третьому році, коли економіка здобула імпульс у вигляді додаткових витрат, використовуємо рівняння
−
Yt = A+c′Yt −1 + k(Yt −1 −Yt −2 ) .
Підставляючи значення змінних, дістаємо:
Y3 = 25 +0,8×105 +0,6(105 −100) = 25 +84 +3 =112 ; Y3 −Y3* =112 −110,25 =1,75 .
Відповідь: розрив між фактичним та трендовим значеннями ВВП у третьому році, спричинений дискреційними змінами сукупних витрат, стано-
вить 1,75.
379

2 Умова
πt = ν0t ,2 ×πte
MP D = 0,1Yt0,3
πe = πe− πt−1 0,15
t t 1 πe− t 1
(a +b)2 −4b — ?
3 Умова
~ |
|
~ |
+0,05 |
|
Gt =1,2Gt −1 |
||||
|
Gt |
= 0,2 |
|
|
~ |
|
= −1,4 |
|
|
Gt −1 |
|
|||
Nt = 48
Nt −1 = 47 g =1,1
ln Gt — ?
4 Умова
~ |
= 2 |
Gt−1 |
|
~ |
= 3 |
At −1 |
Розв’язання
Характер економічних змін— їх монотонність чи коливальність — за моделлю Лайдлера визнача-
ється кількісним значенням виразу |
(a +b)2 −4b , |
||
для якого a = βγ −α ; b = |
α |
. |
|
α+β |
|
||
α +β |
|
|
|
Значення α, β, γ беремо з рівнянь, |
даних в умо- |
||
вах задачі, а саме: α = 0,3 , β = 0,2 , γ = 0,15 . Після підстановки дістаємо: а = −0,54 ; b = 0,6 . Відповідно (a +b)2 −4b = –2,364 < 0.
Відповідь: оскільки кількісне значення виразу (a +b)2 −4b є меншим від нуля, то після імпуль-
су у вигляді додаткової грошової пропозиції економіка буде змінюватися коливально.
Розв’язання
Для розв’язання задачі скористаємося такими
рівняннями моделі |
~Прескотта—Кідленда: |
||
ln Gt = |
Gt |
+(n + g)t +Gt ; |
|
~ |
~ |
|
|
Gt = pGGt−1 +εG . |
|
||
|
|
t |
|
Темп проросту населення становить
n = 48 − 47 100 % = 2,13 % . 47
Імпульсну складову приросту державних витрат
дістанемо з рівняння: |
|
|
|
||
~ |
~ |
~ |
×(−1,4) |
+0,05 |
= −1,63 . |
Gt = |
1,2Gt−1 + 0,05 |
Gt =1,2 |
|||
Тоді |
= 0,2 + (2,13 +1,1) −1,63 =1,8 . |
|
|
||
ln Gt |
|
|
|||
Відповідь: темп приросту державних витрат у поточному році становитиме 1,8 %.
Розв’язання
Скористаємося такими рівняннями моделі Прес-
котта—Кідленда: |
~ |
||
~ |
~ |
~ |
|
Ct = aCK Kt + aCA At + aCGGt ;
380
