Лекция 4. Гармоническая функция. Её связь с аналитической функцией

Определение 4.8.1. Действительная функция двух действительных переменных называется гармонической в области , если она в этой области непрерывна, имеет непрерывные частные производные первого и второго порядков и удовлетворяет уравнению Лапласа:

.

Пример 4.8.1. Показать, что функция является гармонической на всей комплексной плоскости.

Решение. Функция является непрерывной на всей плоскости. Найдём частные производные

, , , .

Эти производные являются непрерывными и удовлетворяют уравнению Лапласа

.

Следовательно, функция является гармонической на всей плоскости.

Пример 4.8.2. Проверить, будет ли функция гармонической.

Решение. Данная функция непрерывна при любом . Найдём её частные производные , , , . Условие выполняется, если , . Таким образом, функция является гармонической только на оси Ox, за исключением точки .

Теорема 4.8.1. Действительная и мнимая части аналитической в области функции являются гармоническими в этой области.

Доказательство. ▶ Пусть функция

w = f(z) = u(x, y) + iv(x, y)

аналитична в D. Это значит, что функции u(x, y) и v(x, y) как функции двух переменных дифференцируемы в D и в каждой точке этой области выполняются равенства

, .

Обе части первого равенства продифференцируем по x

,

а второго – по y

.

Складывая почленно эти равенства, получим

.

Таким образом, функция u(x, y) удовлетворяет уравнению Лапласа. Аналогичное доказательство проводится и для функции v(x, y):

.

Значит функции u(x, y) и v(x, y) являются гармоническими функциями в D. ■

Обратное утверждение, т.е. если u(x, y) и v(x, y) – две гармонические функции, то сумма u(x, y) + iv(x, y), является аналитической функцией, вообще говоря, не имеет места. Однако можно построить аналитическую функцию, задав в качестве её действительной или мнимой части какую-либо гармоническую функцию.

Пример 4.8.3. Найти аналитическую функцию по известной её мнимой части при условии, что .

Решение. Сначала убедимся, что функция гармоническая. Для этого находим её частные производные

, , , .

Подставляя их в уравнение Лапласа, видим, что равенство выполняется. Кроме того, частные производные первого и второго порядков непрерывны во всех точках плоскости. Для отыскания функции воспользуемся условиями Коши – Римана , .

Значит, для определения функции имеем систему дифференциальных уравнений в частных производных

Решая первое уравнение системы, находим

, где функция пока неизвестна. Для её нахождения подставим функцию во второе уравнение и получим

.

Отсюда . Следовательно, .

Итак, искомая функция имеет вид .

Теперь

.

Постоянную найдём из условия , т.е.

, отсюда . Окончательно получаем

.

Определение 4.8.2. Две гармонические функции, связанные условиями Коши – Римана, называются сопряжёнными гармоническими функциями.

§9. Геометрический смысл производной функции комплексного переменного

Рассмотрим функцию f(z), аналитическую в области . Пусть  произвольная точка области и . Чтобы выяснить геометрический смысл производной , представим комплексное число в тригонометрической форме , и выясним геометрический смысл аргумента  и модуля k.

Из аналитичности функции в области следует существование конечного предела

.

Тогда из теоремы 4.5.3 следует существование двух пределов и .

Рассмотрим

. (4.8)

Так как аргумент частного комплексных чисел равен разности аргументов делимого и делителя, то

. (4.9)

Проведём из точки гладкую дугу  (рис. 28). Образом дуги  является дуга , выходящая из точки (рис. 29). Возьмём на  точку , которая отобразится в точку на дуге .

Если по дуге , то по дуге . Из непрерывности функции следует, что приращения и одновременно стремятся к нулю.

В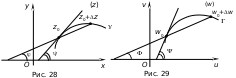 плоскости проведём касательную к кривой точке , а в плоскости – касательную к кривой в точке . Обозначим через  и  углы наклона этих касательных к осям Ox и Ou, соответственно. Обозначим через  угол наклона к оси секущей, соединяющей точки и кривой и через – угол наклона к оси секущей, соединяющей точки и кривой .

Так как , то из равенств (4.8) и (4.9) получаем . Но argw = , argz =  и, следовательно, .

Таким образом,   это угол, на который нужно повернуть касательную в точке к кривой , чтобы получить угол, образованный касательной к кривой в точке .

Рассмотрим теперь предел

.

Так как , то имеем .

Здесь  длина хорды, стягивающей дугу Г с концами в точках и ,  длина хорды, стягивающей дугу  с концами в точках и . Предел называется коэффициентом растяжения в точке . Он показывает во сколько раз длина бесконечно малой дуги на кривой  отличается от длины бесконечно малой дуги на кривой .

Таким образом, при отображении посредством аналитической функции, производная которой отлична от нуля, все бесконечно малые дуги, выходящие из точки , получают одно и то же растяжение, равное . При k > 1 бесконечно малая дуга при отображении удлиняется, а при k < 1 она укорачивается.

На основании вышесказанного можно сделать следующие выводы:

Аргумент производной аналитической функции в точке равен углу поворота дуги  в точке при отображении (при ).

Модуль производной аналитической функции в точке равен коэффициенту растяжения в точке .

Пример 4.9.1. Найти угол поворота  и коэффициент растяжения k в точке при отображении .

Решение: Найдём производную и вычислим её значение в точке . Имеем . Тогда , . Значит, , .