§5. Последовательность комплексных чисел

Последовательностью комплексных чисел называется функция , где – множество натуральных чисел и – множество комплексных чисел. Соотношение называется формулой общего члена последовательности .

Пусть дана последовательность комплексных чисел , где и – некоторые действительные функции целочисленного аргумента .

Определение 4.5.1. Число называется пределом последовательности , если для любого найдётся такой номер , что для всех точки принадлежат -окрестности точки , или, другими словами,

для выполняется условие при ,

для выполняется условие при .

Предел последовательности комплексных чисел обозначается обычным образом: .

Будем также говорить, что последовательность сходится к точке .

Если существует такое действительное число , что для всех справедливо неравенство , последовательность называется ограниченной. Геометрически ограниченность последовательности комплексных чисел означает существование круга конечного радиуса, содержащего все её члены.

Теорема 4.5.1. Всякая сходящаяся к конечному пределу последовательность комплексных чисел ограничена.

Доказательство. ▶ По условию теоремы . Следовательно, при выполняется неравенство , т.е. все члены последовательности , начиная с лежат в некотором круге конечного радиуса. Вне этого круга могут находиться лишь точки , , …, . Но конечное число точек ( ) всегда можно покрыть конечным кругом . Построение круга , содержащего и , показывает ограниченность последовательности . ■

Теорема 4.5.2. Последовательность сходится к числу тогда и только тогда, когда

и .

Доказательство. ▶ Необходимость: Пусть . Это означает, что для любого существует номер такой, что при выполняется неравенство

.

Но тогда при заведомо одновременно выполняются неравенства и , т.е. и .

Достаточность: Пусть и . Тогда для любого найдётся такой номер , что при будут одновременно выполняться неравенства и . Оценим модуль при

.

Таким образом, при выполняется неравенство , т.е. . ■

Из теоремы 4.5.2 следует, что каждой последовательности комплексных чисел соответствуют две последовательности вещественных чисел и . Поэтому многие теоремы и понятия о последовательностях, известные из вещественного анализа, справедливы и для последовательностей комплексных чисел. А именно, если и , то

, , ( ).

Теорема 4.5.3. Пусть , и . Тогда тогда и только тогда, когда и (при соответствующем выборе аргументов).

Доказательство. ▶ Справедливость утверждения теоремы следует из теоремы 4.5.1 и непрерывности функций и , так как , . ■

Пример 4.5.1. Найти предел последовательности , где произвольное конечное комплексное число.

Решение. Рассмотрим пределы и . Находим

.

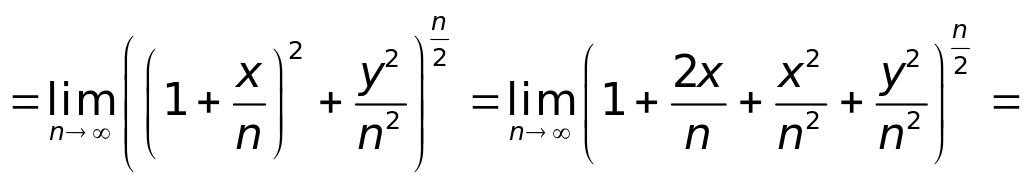
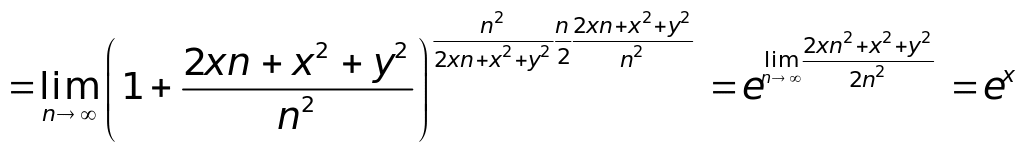Прежде чем вычислять предел , заметим, что при возведении в целую положительную степень комплексного числа его аргумент умножается на эту степень. Поэтому

, .

Находим

.

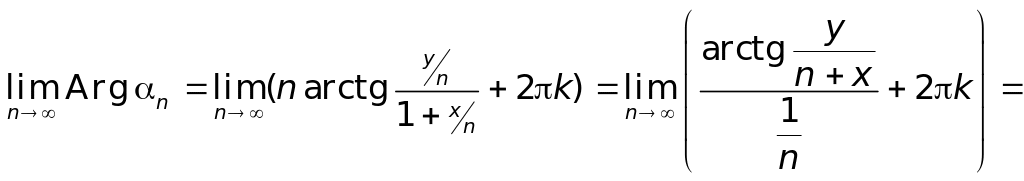
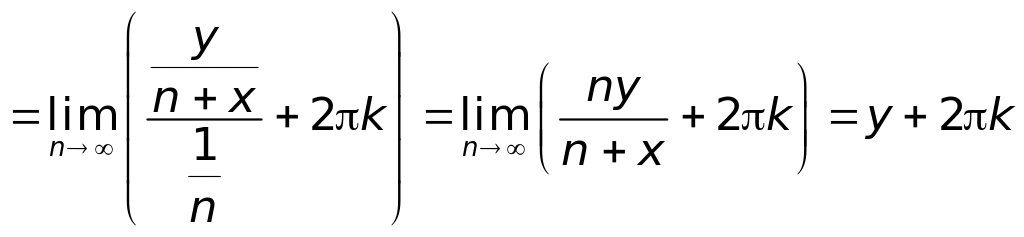Теперь на основании теоремы 4.5.3 можно утверждать, что существует и справедливы равенства , , . Поэтому число можно записать в показательной форме . Таким образом, имеем

.

Отметим, что не имеет смысла вводить символы или для обозначения каких-либо комплексных чисел, так как на расширенной комплексной плоскости имеется только одна бесконечно удалённая точка (см. §3). К этой точке сходятся все последовательности комплексных чисел , для которых одна из последовательностей и или обе из них являются бесконечно большими. В этом случае записывают .