Econometrics

де M E P P P 1 P .

Підставивши цей вираз у співвідношення (5.19), дістанемо:

YS A*Y ,

де A* E D D MD 1 D M .

Отже, здобутий вектор залежної змінної з вилученими сезонними коливаннями також можна подати у вигляді лінійного перетворення вихідного вектора Y. Зауважимо, що в цьому разі матриця А* не буде симетричною, але лишиться ідемпотентною і задовольнятиме умову A*D=0.

5.8. Оцінювання економетричних залежностей

Оцінюючи економетричні залежності на основі квартальних або місячних даних, необхідно передусім з’ясувати, чи не дає змоги економічна теорія дістати такі змінні, які відразу ж можна включити до моделі. Проілюструємо це положення на прикладах.

Приклад 5.2. Робітник щомісяця отримує заробітну плату, яка не містить сезонних коливань, але його споживчі витрати можуть мати ці коливання, і вони досягають свого максимуму у третьому кварталі через відпускні витрати. Щоб знайти залежність між споживчими витратами та заробітною платою, необхідно скоригувати квартальні витрати.

У цьому разі скориговані квартальні витрати можна дістати як функцію від доходу (зарплати) і подати реальні витрати як суму скоригованих витрат і сезонної складової.

Економетрична модель буде тоді моделлю реальних витрат від доходу та необхідної кількості сезонних фіктивних змінних. Але оскільки і сам дохід часто містить сезонні коливання, які не завжди можуть збігатися із сезонними коливаннями в споживчих витратах, то в цьому випадку модель реального споживання від доходу має містити споживчі витрати з вилученою сезонністю. До цієї моделі будуть включені необхідні фіктивні змінні, що відбивають сезонні коливання залежної змінної.

Приклад 5.3. Приймаючи господарські рішення, фірма, визначаючи темп випуску продукції, часто користується «згладженими» значеннями середнього продажу. Тому до відповідної еко-

17

нометричної моделі необхідно включати реальне виробництво як функцію скоригованого на сезонність продажу.

Зауважимо, що в багатьох випадках, особливо на макрорівні, не можна сформулювати достатньо чіткі вказівки щодо того, які з

даних — скориговані чи не скориговані — необхідно включати в економетричну модель, але на практиці проблема специфікації саме з цього боку не є непереборною.

Під час побудови економетричної моделі можна брати змінні із сезонним компонентом і для врахування цього компонента застосовувати фіктивні змінні, а можна спочатку скоригувати вихідні дані, вилучивши сезонний компонент, наприклад за допомо-

гою ковзної середньої чи регресії на одну із матриць D або PD .

Зауважимо, що коли сезонні коливання дуже сильні, тоді потрібно зосередитись на специфікації моделі і внести необхідні корективи.

5.9.Коваріаційний аналіз

Упопередньому підрозділі ми ввели аналіз дисперсій, що дає змогу простежувати, як загальна сума квадратів відхилень розбивається на суму квадратів регресії, яка пояснюється множиною

пояснювальних змінних, і суму квадратів залишків. Можна також показати, що суму квадратів регресії можна розбити також на окремі складові відхилень, зумовлені лише частиною пояснювальних змінних. Це особливо важливо, якщо використовуються групові дані спостережень.

Важливо знати, чи суттєві відмінності між груповими серед-

німи змінної Y. Звичайно, варіація змінної Y всередині групи відбиває природні характеристики стохастичної компоненти Y і може бути використана для оцінювання варіацій групових середніх.

Загальна варіація змінної Y складається із суми варіацій між групами і варіацій у межах груп:

18

Оскільки групи спостережень формуються залежно від певних ознак змінної Y, то різниця між груповими середніми характеризує ефект групових різниць між значеннями Y за рахунок ознак групування, а також некерованих чинників.

Наприклад, розглядаються дві групи спостережень над змінними Y і X, де Y — залежна, X — пояснювальна змінна. Для кожної з груп можна побудувати регресію Y за X, тобто: Y1 X1a u1 і

Y2 X 2a u2

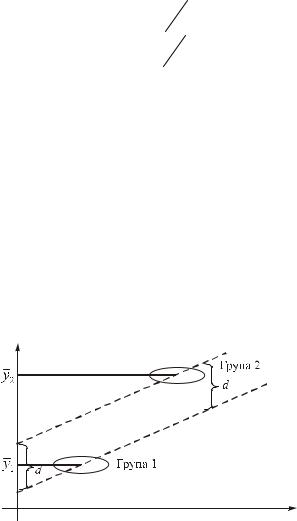
Фактичні дані змінної X для групи 2 значно більші, ніж для групи 1. Отже, звичайна різниця між груповими середніми буде грубою верхньою оцінкою ефекту групування, що на рис. 5.2 показано різницею d між паралельними лініями регресії. Якщо значення змінної X однакові для обох груп, то еліпси розміщуються вертикально один над одним і тоді різниця між y2 – y1 наближа-

ється до d. Зауважимо, що ефект групування оцінюється вільним членом регресії.

Рис. 5.2. До унаочнення ефекту групових різниць

19

Якщо кожна з груп має вплив некерованих чинників, то коваріаційний аналіз дає змогу знайти статистичні поправки на їхній вплив, бо некеровані чинники важко виміряти для окремих груп. Для проведення такого коригування природно припустити, що змінна X має одну й ту саму силу впливу на залежну змінну в обох групах. Але це припущення варто перевірити. Наприклад, чи мають виробничі функції цукру в різних регіонах України одну й ту саму граничну ефективність; чи показує функція попиту на певний товар однакові оцінки параметрів для різних соціальних груп; чи не змінюються оцінки параметрів моделі споживання для різних часових періодів?

На ці запитання можна відповісти, застосувавши коваріаційний аналіз у таких випадках:

1)для перевірки статистичної значущості різниці у вільних членів моделі;

2)для перевірки статистичної значущості різниці в оцінках

інших параметрів моделі; 3) для перевірки статистичної значущості різниці в загальному

вигляді співвідношень для груп, коли нехтують різницями між усіма оцінками параметрів моделі.

Нехай необхідно побудувати економетричну модель на основі

s – 1 — кількість некерованих пояснювальних змінних. Розмір вибіркової сукупності спостережень включає m=n·s

елементів вибірки.

Розглянемо найпростішу модель залежності на основі цих даних:

Y=XA+v. (5.22)

У цій моделі:

Y — вектор залежної змінної розміру m 1;

X — матриця пояснювальних змінних розміру m r;

A — вектор оцінок параметрів моделі розміру (r+1) 1; v — вектор залишків.

Перший стовпець матриці X, як і звичайно, складається з m одиниць і необхідний для визначення вільного члена моделі. Рівняння (5.22) фактично означає, що розбивати інформацію на гру-

20

пи недоцільно, бо варіація Y від варіації X приблизно однакова для кожної групи. Але дослідник не має впевненості стосовно того, що це так насправді, і хоче переконатися, чи не відбивається ефект групування на вільному члені моделі.

У цьому випадку будується загальніша модель:

де Y, X і A мають той самий зміст, що й раніше, В – вектор розміру s 1, а D — матриця фіктивних змінних розміру ns (s – 1), u— вектор залишків.

Кожний стовпець матриці D утворено із s підвекторів розміру n. Із моделі (5.23) випливають такі співвідношення для груп:

Як бачимо, в моделі різняться тільки вільними членами, а параметри j спільні для всіх груп. Якщо ефект групування не позначається на значенні вільного члена, то 2 3 ... s 0. У

21

цьому разі необхідно перевірити гіпотезу, чи відрізняються s

від нуля, на основі t-критерію.

Нехай за методом найменших квадратів дістали:

€

Y XA v,

дом найменших квадратів. Помноживши наведене рівняння ліво-

Аналогічно, застосовуючи метод найменших квадратів до

(5.23), маємо:

Різниця між залишковими сумами квадратів для (5.22) і (5.23) така:

€ € € . v v u u B D Y AX Y A X Y

Подамоковаріаційнийаналіздлярізнихвільнихчленівутабл.5.2.

22

Перевірка нульової гіпотези щодо вектора € здійснюється за

допомогою F-статистики:

B

групах. Але умову, що передбачає рівність елементів a€j для різ-

них моделей, необхідно перевірити.

Припустимо тепер, що в економетричних моделях, які будуються для різних груп спостережень, будуть різними не лише вільні члени, а й інші оцінки параметрів. Кількісно це означає, що необхідно розглядати побудову моделі на основі статистичної інформації за окремими групами.

Тоді вибіркові дані для k-ї групи запишуться:

Вектор одиниць включається в кожну з матриць пояснювальних змінних Xk.

Модель для групових даних запишеться у вигляді:

23

Якщо s матриць пояснювальних змінних Xk об’єднати в блоч- но-діагональну матрицю

то множину економетричних моделей можна записати рівнянням:

де С — вектор розміру sr, що містить s підвекторів, а u — вектор залишків розміру ns, який містить s підвекторів uk.

Вектор C в цьому разі визначається так:

Залишкова сума квадратів моделі (5.28) дорівнює u u . Ця

сума квадратів менша за суму квадратів залишків u u , наведених у таблиці 5.2, оскільки ми ввели в регресію додаткові параметри. Зміна залишкової суми квадратів свідчить про той внесок у суму квадратів регресії, який могли б зробити оцінки параметрів C2, … Cs від однієї групи до іншої.

Чи є цей внесок істотним, статично значущим, можна переві-

рити за допомогою суми квадратів залишків u u .

Згідно з розрахованими дисперсіями визначаються наведені далі F-критерії.

1. Критерій для оцінювання статистичної значущості вільних

24

2. Критерій для перевірки статистичної значущості оцінок па-

Якщо гіпотезу про однорідність оцінок параметрів b2, …, bs, здобутих для різних груп даних, не буде відхилено, то можна перейти до перевірки відмінностей у вільних членах.

Нарешті можна виконати перевірку однорідності всіх моделей у цілому за всіма групами, порівнявши різниці залишкових сум

25

Аналогічно можна перевіряти відмінності деякої підмножини параметрів для s груп спостережень.

Зауважимо, що це робиться через побудову моделі з обмеженнями, які враховують однорідність моделей, але водночас досліджується зміна решти параметрів для різних груп спостережень.

Приклад 5.4. Нехай потрібно побудувати економетричну модель, яка характеризує залежність споживання безалкогольних напоїв від доходів, використовуючи квартальні дані за п’ять років. На споживання безалкогольних напоїв впливають природно-кліматичні умови, тобто весняно-літній та осінньо-зимовий періоди, тому необхідно дляпобудови моделі використати фіктивні змінні.

Подамо ці дані в таблиці 5.4.

Таблиця 5.4

26