
кинематика
.pdfЛекция 1. КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 1.1. Предмет кинематики
Кинематика − это раздел физики, посвящённый математическому описанию движения без анализа причин, приводящих к его возникновению или изменению. Причиной изменения или возникновения поступательного движения является сила, а сила по II закону Ньютона связана с массой. Поэтому для того, чтобы исключить из рассмотрения силу достаточно не рассматривать массу. При этом кроме силы из рассмотрения выпадают многие механические понятия: импульс, энергия, момент импульса. А что остаётся, то и рассматривается в кинематике. Таким образом, кинематику можно было бы назвать механикой без массы.
Самый простой объект, способный двигаться − это материальная точка: тело, размеры которого пренебрежимо малы в условиях данной физической задачи. Движением материальной точки называется смена её положения с течением времени. Поэтому первое кинематическое понятие, с которым мы сталкиваемся − это положение.
§ 1.2. Вектор положения
Положение чего угодно невозможно задать само по себе. Всё находится относительно чего-то. Значит, мы должны сначала установить начало отсчёта (точку О), а это невозможно сделать подругому, кроме как поставив туда какое-либо материальное тело (тело отсчёта). И от этого «главного» тела уже можно проводить геометрические векторы, соединяющие начало отсчёта с тем или иным положением материальной точки М (рис.1.1). Геометрическим вектором называется направленный отрезок, соединяющий положения двух материальных точек. Геометрический вектор, соединяющий тело отсчёта с материальной точкой, называется вектором положения материальной точки.
Как правило, с телом отсчёта связывают наблюдателя, который может наблюдать вокруг себя, например, различные положения. Наблюдателей может быть много, и каждый видит своё. То, что одинаково для всех наблюдателей, называется абсолютным. То, что может быть разным для разных наблюдателей, называется
относительным.

При задании положения материальной точки относительно тела отсчёта последнее по определению считается неподвижным. Поэтому все возможные векторы положений начинаются из одной точки и называются радиус-векторами r .
Рис.1.1
Радиус-вектор не является геометрическим в общем случае, потому что может соединять тело отсчёта с пустотой.
Совокупность всех возможных радиус-векторов образует
пространство.
Смена начала отсчёта приводит к изменению всех радиусвекторов. Каким образом? Ответ зависит от системы постулатов, которыми мы собираемся пользоваться. Классическая механика, которую мы в основном и изучаем, использует постулаты ГалилеяНьютона.
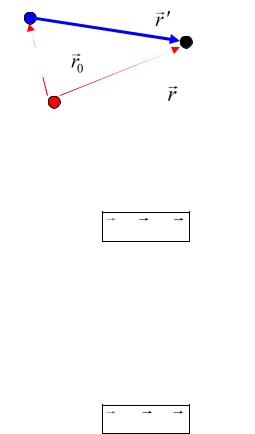
Если положение материальной точки М относительно тела отсчёта в точке О обозначить r (рис.1.2 левый), относительно другого тела отсчёта в точке О' обозначить r (правый рисунок), а геометрический вектор, соединяющий точки О и О', обозначить r0 ,
то наблюдатель в точке О будет видеть три геометрических вектора: |
||||
|
|
|
|
|
r , |
О М |
и |
r0 |
(левый рисунок), связанных правилом сложения |
векторов по треугольнику.

Рис
1.2
Пусть другому наблюдателю в точке О' нет дела ни до чего, кроме материальной точки М. В дальнейшем нелюбопытному
наблюдателю будет отводиться «второстепенная» роль. В
противовес этому наблюдатель, который видит всё, будет считаться |
|
|
|
«основным». В общем, наблюдатель О' видит только один вектор r |
|
(правый |
рисунок). Как соотносится геометрический вектор r , |
|
|
видимый |
в пространстве О', с геометрическим вектором О М , |
видимым в пространстве О? Ответ на этот вопрос даёт первый
постулат Галилея: |
|
|
|
||||
|
|
|
|
геометрические векторы абсолютны. |
|||
То |
|
есть, |
|
(подчеркнём, |
что соотношение |
тождества |
|
|
О М = r |
||||||
|
|
|
|
|
|
, он такой |
|
О М r здесь неуместно: О М не |
тот же самый, что r |
||||||
же). Тогда предыдущие рисунки можно переделать так:
Рис.1.3
И правило сложения векторов по треугольнику позволяет записать соотношение между тремя векторами:
r= r + r0 .
Всоответствии с этим соотношением можно находить положения в «основном» пространстве, зная их во «второстепенном». Такое преобразование радиус-векторов будем называть обратным преобразованием Галилея. Соответственно, прямое преобразование позволяет находить положения во «второстепенном» пространстве, зная их в «основном»:
r= r − r0 .
Вдальнейшем какая-либо величина в «основном» пространстве будет называться «абсолютной», во «второстепенном» пространстве
− «относительной», а та, через которую они связаны, − переносной. |
||
Значит |
|
|
• |
|
−«абсолютный» радиус-вектор; |
r |
||
• |
|
|
r −«относительный» радиус-вектор; |
||
• |
|
− переносный радиус-вектор. |
r0 |
||

Обратим внимание на кавычки, подчёркивающие переносный смысл слов «абсолютный» и «относительный».
Итак, в соответствие с первым постулатом Галилея смена начала отсчета приводит к изменению пространства, которое описывается преобразованием Галилея. Это означает, что
пространство относительно.
§ 1.3. Скорость движения |
|
|
Используя понятие радиус-вектора, движение можно описать |
||
функциональной зависимостью |
|
(t ), где t− время. Поскольку |
r |
||
положение относительно, то и движение относительно. Относительны и все понятия, связанные с ним. Первым из таких понятий мы рассмотрим скорость движения.
Скоростью движения материальной точки называется скорость изменения её положения. Понятно, что скорость движения
− это вектор, который реализуется в данный момент времени. То
( )
есть, мы должны определить векторную функцию от времени t
как скорость изменения функции ( ). Что такое мгновенная r t
скорость изменения нужно хорошо обдумать. И стартовой точкой наших размышлений должно стать понятие средней скорости движения, которое абсолютно очевидно.
Прежде всего, введём понятие перемещения. Перемещением называется изменение положения, иначе говоря, разница положений в моменты времени, который стал, и который был:
r = r (t + t )− r (t ).
Исходя из правила треугольника, легко доказать, что вектор r начинается в старом положении и заканчивается в новом.
Средней скоростью движения называется отношение перемещения к промежутку времени, в течение которого оно произошло:

 = rt .
= rt .
Опираясь на данное, сформулируем искомое определение.
Мгновенной скоростью движения называется средняя скорость движения за достаточно малый промежуток времени. Сразу возникает вопрос: достаточно малый для чего? Ответ следующий: для нашей точности измерения, построения и вычисления. Как это?
Дадим ещё одно определение (поначалу их всегда много). Траекторией называется совокупность положений, пройденных телом в процессе движения. Тело не может в один и тот же момент времени находиться в разных положениях. Поэтому траектория движущегося тела представляет собой линию, и при этом линию непрерывную. Она может быть ломанной, но мы будем иметь в виду только гладкие траектории. В зависимости от формы траектории различают прямолинейное и криволинейное движение. Если криволинейная траектория лежит в одной плоскости, то движение называется плоским, если нет − объёмным или пространственным.
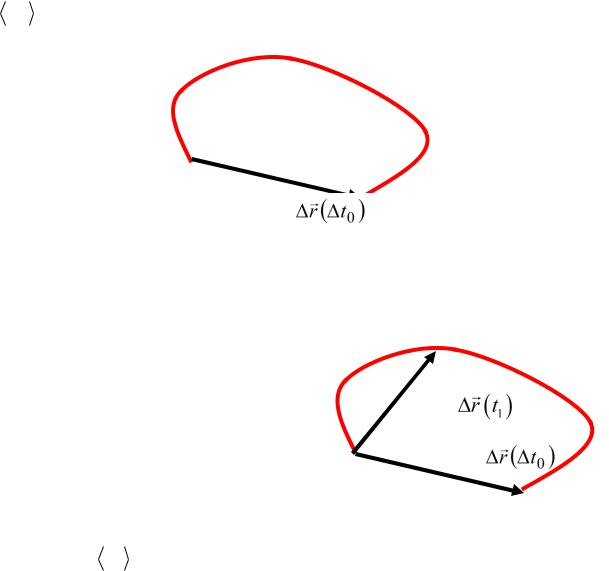
Изобразим плоскую траекторию, которую прошло тело между моментами t и t + t0 , а также перемещение тела за промежуток
времени |
t |
(рис.1.4а) и вычислим среднюю скорость |
||||||
|
|
|
|
r ( t00) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|||||
|
0 |
= |
|
|
|
|
|
. |
|
|
t0 |
||||||
|
|
|
|
|
||||
Рис.1.4а
Можно ли считать промежуток времени t0 достаточно малым? Мы
не знаем, пока не сделаем следующего шага. Но мы знаем направление, в котором должны делать этот шаг: мы уменьшим промежуток времени, например,
поделим его пополам: t1 = t0 / 2, |
|
|||||||||||
и, зная положение тела на |
|
|||||||||||
траектории |
|
в любой |
момент |
|
||||||||
времени, построим перемещение за |
|
|||||||||||
этот уменьшенный |
промежуток |
|
||||||||||
времени (рис. 1.4б). А также |
Рис. |
|||||||||||
вычислим |
|
новую |
среднюю |
|||||||||
|
|
|
|
|
|
|
r ( t ) |
|
|
|
1.4б |
|
|
|
|
|
|
|
|
|
|||||
скорость |
|
|
|
= |
|
|
|
1 |
|
|
. Теперь |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
t1 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
мы можем сказать, |
был ли промежуток времени t0 достаточно |
|||||||||||
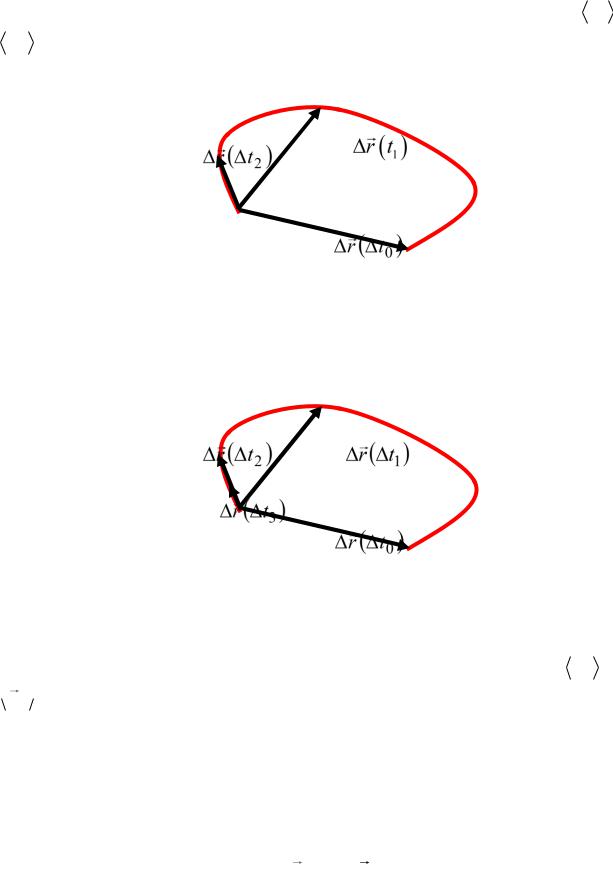
малым: не был, потому что мы видим, что и перемещения |
|
( t ), |
r |
||
|
|
1 |
r ( t0 ) явно не совпадают друг с другом, и средние скорости |
1 , |
|
|
|
|
0 тоже. |
|
|
Делаем следующий шаг: t2 = t1 / 2, строим, вычисляем:
Рис.1.4в
Теперь мы можем сказать, что промежуток времени t1 тоже был
недостаточно малым.
Делаем следующий шаг:
Рис.1.4г
Стоп! Мы видим, что при нашей точности измерений и построений |
||
|
|
|
направления перемещений r ( t3 ) и |
r ( t2 ) совпадают. Это |
|
|
|
|
значит, что направления совпадают и у средних скоростей 3 |
и |
|
 2
2 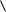 . Если при этом с нашей точностью вычислений совпадают и их модули, то можно сказать, что промежуток времени t2 достаточно мал. Дальнейшее уменьшение промежутка времени не приведёт к заметному для нас изменению средней скорости движения, и мы можем сказать, что с доступной для нас точностью мы определили мгновенную скорость движения:
. Если при этом с нашей точностью вычислений совпадают и их модули, то можно сказать, что промежуток времени t2 достаточно мал. Дальнейшее уменьшение промежутка времени не приведёт к заметному для нас изменению средней скорости движения, и мы можем сказать, что с доступной для нас точностью мы определили мгновенную скорость движения:
(t ) =  2
2 

И достаточно малое изменение аргумента |
t , |
и изменение |
|||
|
|
|
(t ), связанное с таким |
изменением |
|
функции r |
= r |
(t + t )− r |
|||
аргумента, мы будем называть элементарными (в математическом смысле). В математике они называются бесконечно малыми. И в физике, и в математическом анализе элементарные изменения называются дифференциалами и обозначаются заменой греческой буквы на латинскую букву d: элементарный промежуток времени dt, элементарное перемещение dr . Элементарному противопоставляется понятие конечного: не в том смысле, что меньше бесконечного, а в том смысле, что не является бесконечно малым.
По определению отношение дифференциала функции к дифференциалу аргумента называется производной функции:
r (t ) = drdt .
Таким образом, пользуясь языком высшей математики, мы можем сказать, что
мгновенная скорость движения или просто скорость движения является первой производной радиус-вектора по времени.
(t ) = r (t ) = drdt = r .
Впоследнем равенстве использовано самое компактное
обозначение производной по времени: точка над функцией, являющееся общепринятым в механике.
Обращаем Ваше внимание, на то, что в данный параграф вообще не касается вопросов относительности, поэтому штрихи здесь − это не знак второстепенности, а обозначение производной.
§ 1.4. Относительность скорости движения
В этом параграфе мы будем пользоваться понятием системы отсчёта, хотя не будем иметь на это права. Из всех атрибутов системы отсчёта раньше был введено только начало отсчёта. Другой атрибут − часы, находящиеся в начале отсчёта. Пусть двое часов находились
водной системе отсчёта, а потом «разошлись» по разным. Находясь
водном месте, они были синхронизованы. Как повлияет на их показания относительная скорость? Ответ на это опять зависит от выбора системы постулатов. В механике Ньютона-Галилея
«работает» второй постулат Галилея: об абсолютности промежутков времени. Согласно этому постулату,
показания часов не зависят от их относительной скорости.
Вспомним |
обратное |
преобразование Галилея |
для радиус- |
|||
|
|
|
|
|
|
|
векторов: |
r = r |
+ r0 . |
Возьмём |
элементарные |
изменения |
|
(дифференциалы) от обеих частей этого равенства. |
|
|||||
dr = d (r + r0 ) |
dr = dr + dr0 . |
|
|||
Поделим это равенство на элементарный промежуток времени |
|||||
dt по часам «основного» |
наблюдателя, |
в |
течение |
которого |
|
произошли элементарные |
перемещения |
dr |
и dr . |
Равенство |
|
|
|
|
|
0 |
|
останется верным:
drdt = drdt + drdt0 .
В соответствие со вторым постулатом Галилея dt=dt', где dt' − промежуток времени по часам «второстепенного» наблюдателя, в течение которого материальная точка переместилась относительно него на dr . Значит, можно записать:
drdt = drdt + drdt0 .
Это обратное преобразование скорости по Галилею:
= + 0 .
Прямое преобразование скорости:
= − 0 .
§1.5. Траектория движения
Если траектория представляет собой пространственную кривую, то в каждой точке траектории можно ввести понятие
соприкасающейся плоскости. Соприкасающейся плоскостью в
какой-либо точке траектории М называется предельное положение плоскости, проходящей через три точки N, M, P этой траектории, когда точки N и P неограниченно приближаются (стремятся) к точке
М (рис.1.5).
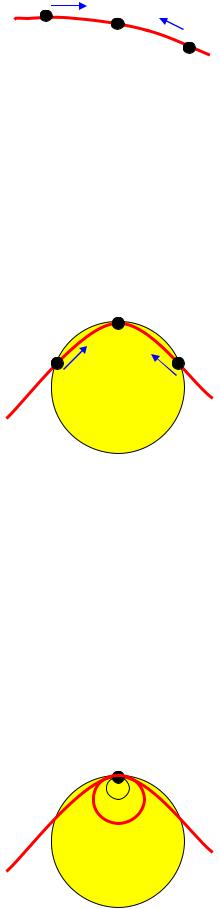
Рис.1.5
Через три точки, не лежащие на одной прямой, можно провести не только единственную плоскость, но и единственную окружность. Поэтому для любой точки криволинейной траектории можно ввести понятие соприкасающейся окружности.
Соприкасающейся окружностью в какой-либо точке траектории М называется предельная окружность, проходящая через три точки N, M, P этой траектории, когда точки N и P неограниченно приближаются (стремятся) к точке М (рис.1.6).
Рис.1.6
Центром и радиусом кривизны траектории в точке М называется центр и радиус кривизны окружности, соприкасающейся с траекторией в точке М.
Ни в коем случае не нужно путать понятие соприкасающейся окружности в данной точке траектории и окружности, касающейся траектории в данной точке. В точке М траектории может касаться бесконечное количество окружностей, и только одна из них будет соприкасающейся. Эта такая окружность, которая вблизи точки касания неотличима от самой траектории. На рисунке 1.7 − это окружность среднего размера.
Рис.1.7
Очевидно, что в случае пространственной траектории соприкасающаяся окружность лежит в соприкасающейся плоскости. Прямолинейную траекторию можно считать траекторией с бесконечным радиусом кривизны.
Дадим важное определение. Орт − это вектор, не обладающий физической размерностью (безразмерный), модуль которого равен единице. Любой вектор можно представить, как произведение модуля на орт. Например, радиус-вектор:
r = r ρ .
Значит, орт любого вектора равен частному от деления вектора на его орт:
ρ = r .
r
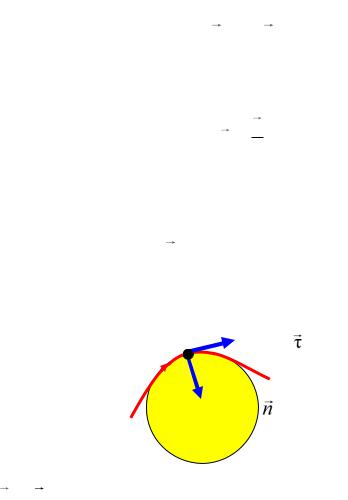
Нормалью траектории n в точке М называется орт, направленный из точки М в центр кривизны траектории в точке М
(рис.1.8).
Ортом касательной τ в точке траектории М называется орт, касательный к соприкасающейся окружности в точке М и направленный по движению.
Рис.1.8
Ясно, что τ п .
В случае если ни один конечный отрезок траектории не проходился материальной точкой дважды, путь или путевая координата s(t) − это длина траектории от точки начала отсчёта пути до положения в данный момент времени. В противоположном случае это определение не годится: для спортсмена, который наматывает круги на стадионе, длина его траектории совсем не равна
преодолённому им пути. |
|
|
|
Отметим две точки на траектории: M с радиусом-вектором r1 |
|
|
|
и N с радиусом-вектором r2 |
(рис.1.9а). |
