кинематика

r s

(равенство выполняется в случае прямолинейной траектории). Очевидно (рис.1.9б), что, во-первых, элементарное перемещение из точки М касательно к траектории в этой точке, то есть,

а во-вторых, что

dr = ds ,

Рис.1.9б

где ds− элементарный путь, пройденный материальной точкой из положения М. Значит,

Мы вывели это равенство для криволинейной траектории, само собой, оно выполняется и для прямолинейной. Таким образом, мы имеем связь между элементарными перемещением и приращением пути на произвольной траектории:

dr = ds τ .

Разложение вектора на два избранных направления представляет собой геометрическую операцию, противоположную операции сложения двух векторов по правилу параллелограмма. На языке чистой геометрии задачу можно сформулировать так: нужно построить параллелограмм по заданной диагонали и направлениям смежных сторон.

вдоль данных направлений (рис.1.10).

Рис.1.10

Геометрические действия сводятся к тому, чтобы из конца вектора проводить линии, параллельные одному из ортов до пересечения с линией действия второго. То есть, для того чтобы построить составляющую вектора на одно из двух произвольных направлений, нужно держать в голове сразу оба направления.

Из бесконечного множества вариантов выбора возможной пары направлений выделим случай, когда они взаимно перпендикулярны. Разложение вектора на взаимно перпендикулярные направления

называется проецированием, или построением векторов проекций. Для того чтобы построить вектор проекции, в

отличие от вектора составляющей достаточно одной оси: той, на которую проецируется вектор. Из конца вектора опустим перпендикуляр на

ось (Рис.1.11). Точка пересечения перпендикуляра с осью является концом вектора проекции. При этом нужно твёрдо помнить, что векторы проекций являются составляющими вектора, только если направления, на которые производится проецирование, взаимно перпендикулярны.

Проекцией вектора на данное направление называется модуль вектора проекции, снабжённый знаком. Правило знака следующее: если вектор проекции сонаправлен с ортом направления, то проекция положительна; если вектор проекции направлен

( ,n1 ) = n1 cosα = cosα = 1 .

То есть,

проекция вектора на данное направление равна скалярному произведению вектора на орт направления.

n = ( ,n).

Разложение вектора скорости вводится по определению, а с определениями не спорят. Но вполне можно задать себе вопрос: а зачем? Есть ли какой-нибудь физический смысл в таком действии? Есть ли физический смысл в скоростях относительно Земли, сумма которых дала бы полную скорость тела относительно Земли? Положительный ответ на этот вопрос даёт закон относительности скорости Галилея.

Возможна ситуация, когда «относительная» скорость в законе Галилея

не зависит от переносной. Например, скорость поперечной подачи резца в токарном станке (скорость резца относительно суппорта) не зависит от продольной подачи (скорости суппорта относительно станка). Это не всегда случается: «относительная» скорость мухи, пролетающей мимо суппорта, может зависеть от того, с какой

наблюдателя относительно основного не зависит от скорости тела относительно второстепенного. Если исчезнет «относительная»

скорость , то тело вместе с второстепенным наблюдателем будет

двигаться относительно основного со скоростью 0 . Всегда можно

выбрать направления 0 и вдоль по осям 1 и 2 или наоборот.

Таким образом, роли составляющих 1 и 2 полной «абсолютной»

скорости будут играть независимые друг от друга «относительная» и переносная скорости. Значит,

относительность скорости по Галилею придаёт математическому действию разложения скорости физический смысл.

Суперпозицией в физике называется сумма независимых слагаемых. Если происходит суперпозиция, то каждое слагаемое суммы «не чувствует» других, подобно тому, как жёлтый цвет не

чувствует синего, смешиваясь с ним в зелёный. Обратная ситуация возникает, когда реагенты, вступая в химическую реакцию, «складываются» в новое вещество: кислород в молекуле воды из-за наличия водорода совсем не тот, что в свободном состоянии. Отсюда понятно, почему разложение вектора скорости на составляющие называется принципом суперпозиции движений.

в том, что в первую формулу входят скорости тела относительно разных систем отсчёта, а во второй фигурируют скорости относительно одной СО.

Знаете, в различных механизмах используются всякие тела, размеры которых остаются неизменными. Это, прежде всего, натянутые нити (верёвки, канаты и т.д.) и стержни. Так вот, для их кинематики очень важным является следующее определение. Полной скоростью в данном направлении называется вектор проекции полной скорости на данное направление. Полная скорость может быть суммой нескольких независимых скоростей. Тогда полное движение в данном направлении будет определяться суммой векторов проекций каждого движения по отдельности, поскольку

вектор проекции суммы равен сумме векторов проекций.

Очевидно следующее утверждение:

если протяжённое тело не меняет своей длины, то полные скорости в направлении этой длины на двух её концах должны быть одинаковы.

§ 1.7. Ускорение

По определению ускорением материальной точки называется первая производная по времени скорости движения, то есть вторая производная по времени радиус-вектора:

Первое слагаемое связано только со скоростью изменения величины скорости движения. Так как эта часть полного ускорения направлена по касательной, то она называется касательным ускорением aτ .

Второе слагаемое связано только с изменением направления скорости движения. Изобразим два положения материальной точки на траектории, разделённые элементарным приращением пути ds, и

Рис.1.12

Соединим положения с центром кривизны траектории в точке dS. Малый угол d между радиусами совпадает с углом между ортами касательной как острые углы с взаимно перпендикулярными сторонами. Из правого рисунка видно, что dτ направлен перпендикулярно τ , то есть по орту нормали, а его величина

dτ = τ dα = dα ,

где выражен в радианах. Следовательно, dτ = dα n .

Угол d связан с элементарным приращением пути ds=R d , где R −

Тогда вторая часть полного ускорения имеет вид:

Так как эта часть ускорения направлена по нормали, то она называется нормальным ускорением.

Сведём все формулы вместе:

§ 1.8. Система координат

Для количественного описания движения в пространстве необходимо введение координат точки, то есть совокупности чисел, однозначно определяющей положение материальной точки

относительно начала отсчёта. Это возможно только в случае введения третьего атрибута системы отсчёта: системы координат. Теперь можно дать определение системы отсчёта: системой отсчёта называется система координат, в начале которой находится тело отсчёта (наблюдатель), снабжённое часами.

В одномерном пространстве для задания «адреса» материальной точки достаточно одного числа, в двумерном пространстве − двух чисел, в трёхмерном − трёх чисел. Способов введения адресации − не один. Например, на плоскости можно задать полярную систему координат (угол, длина радиус-вектора), в пространстве сферическую (длина радиус-вектора, азимутальный угол и угол горизонта). Мы остановимся на подробном рассмотрении системы координат, связанной с разложением радиусвектора.

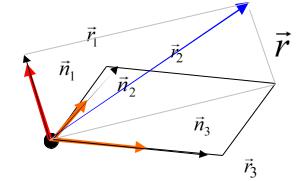
Известно, что любой вектор может быть представлен как сумма трёх векторов, направленных по трём наперёд заданным

координатных осей (рис.1.13). Она называется базисом системы отсчёта. По определению ri − совокупность координат радиус-

вектора в этом базисе. Так как вектор по трём избранным направлениям раскладывается однозначно, то однозначно и определение координат точки пространства.

сумма диагональных элементов совсем проста: a1b1 + a2b2 + a3b3 . Все остальные (перекрёстные члены) кроме произведения координат

(по определению скалярного произведения). Выражение скалярного

произведения ( ) можно существенно упростить, если выбрать a, b

Именно в силу простоты записи скалярного произведения ортогональный базис является предпочтительным.

Впервые ортогональную систему координат (СК) ввёл Р.Декарт, и она называется декартовой. Только в декартовой СК

• координаты вектора являются его проекциями на соответствующую ось: = ( ).

ai a, ni

Докажем это для первой координаты:

(a,n1 ) = (a1n1 + a2n2 + a3n3 ) n1 =

=a1 (n1,n1 )+ a2 (n1,n2 )+ a3 (n1,n3 ) = a1 (n1,n1 ) = a1 .

•координаты вектора связаны с его модулем соотношением Пифагора:

Таким образом, разложение радиус-вектора в декартовой СК будет иметь вид:

r = xi + yj + zk .

( )

Векторную функцию движения r t можно заменить тремя скалярными зависимостями координат от времени, которые называются законами движения: x(t ); y(t ); z (t ). Законы движения

содержат всю информацию о движении. То есть, если известны законы движения, то можно ответить на любой вопрос, касающийся движения материальной точки.

• Скорость.

Таким образом,

проекции вектора скорости равны производным соответствующих законов движения.

• Ускорение.

Таким образом,

проекции вектора ускорения равны вторым производным законов движения.

А как найти касательное и нормальное ускорения? Они являются результатом разложения вектора полного ускорения по направлениям касательной и нормали:

a = aτ + an = aτ τ + ann .

Касательный орт и орт нормали являются осями двумерного ортогонального базиса. То есть алгебраическое значение