4. ПЕРПЕНДИКУЛЯР К ПЛОСКОСТИ
1.Прямая, перпендикулярная плоскости.
2.Определение расстояния от точки до плоскости.
3.Взаимно перпендикулярные плоскости.
1. Прямая, перпендикулярная плоскости
Прямая линия перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости.
Для того чтобы прямая была перпендикулярна к плоскости, необходимо и достаточно, чтобы на чертеже ее горизонтальная проекция была перпендикулярна к горизонтальной проекции горизонтали, а фронтальная проекция прямой – перпендикулярна к фронтальной проекции фронтали.
К1 (К1А1) h1(А1D1) К2 (К2А2) f2(А2B2) К (КА) h и (КА) f
В случае, если плоскость задана следами, то, учитывая, что горизонтальная проекция горизонтали (h1) всегда параллельна
горизонтальному следу Г1, а фронтальная проекция фронтали
параллельна фронтальному следу Г2, то чтобы из точки К (К1, К2) провести прямую перпендикулярно к плоскости Г, необходимо его горизонтальную проекцию провести перпендикулярно к горизонтальному следу Г1, а фронтальную проекцию –
перпендикулярно к фронтальному следу Г2.
К1 (К1А1) Г1(h1) К2 (К2А2) Г2(f2) К (КА) h и (КА) f
2. Определение расстояния от точки до плоскости
Определить расстояние от точки А до плоскости Г, расположенной перпендикулярно к горизонтальной плоскости проекций.
(АВ) Г
(А1В1) Г1; (А2В2) Г2
(А1В1)∩Г1=В1
Определить расстояние от точки А до плоскости общего положения Г, заданной следами.
Отрезок А1К0 есть расстояние от точки К до плоскости Г .
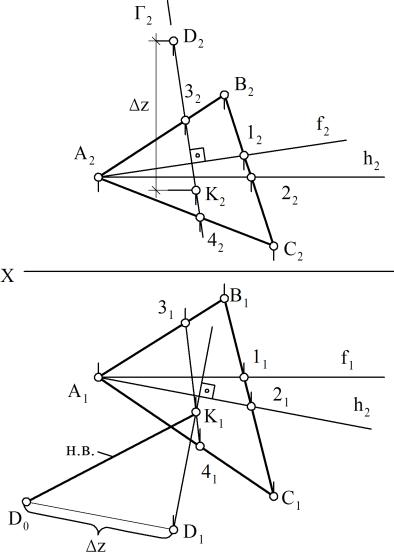
Определить расстояние от точки D до плоскости, заданной треугольником АВС.
Чтобы провести из точки D (D1, D2) перпендикуляр к плоскости треугольника АВС (А1В1С1, А2В2С2) необходимо в первую очередь в плоскости провести фронталь f (f1, f2) и горизонталь h (h1, h2). Фронтальная проекция перпендикуляра проведена из проекции точки D2 перпендикулярно f2, а горизонтальная – из проекции точки D1 перпендикулярно h1. Точка пересечения К (К1, К2) перпенди- куляра с плоскостью треугольника найдена при помощи фронтально-проецирующей плоскости Г (фронтальный след Г2). Натуральная величина расстояния К2D0 определена путем построения прямоугольного треугольника D2K2D0.
