II. Действия на иррациональными числами

Приближенное значения иррациональных чисел по недостатку и по избытку являются конечными десятичными дробями. Поэтому можно определить операцию сложения на множестве I₊.

Определение. Суммой положительных иррациональных чисел a и b, таких, что и , называется число a +b, которое удовлетворяет условию

Найти сумму этих чисел с точностью до 0,01 и 0,001.

III. Умножение положительных иррациональных чисел

Пусть даны числа a и b, которые принадлежат множеству положительных иррациональных чисел. Произведением чисел a и b называется число a^.b. , где a_n и b_n – приближенные значения a и b с точностью до по недостатку, а a_n’ и b_n’ – приближенные значения a и b с точностью до по избытку.

Пример. Найдем произведение с точностью до 0,01.

IV. Аксиоматика множества положительных действительных чисел

Определение. Положительные рациональные числа – числа, которые могут быть записаны в виде бесконечных десятичных дробей. Но десятичная дробь – одна из форм записи действительных чисел. Существует бесконечные двоичные, бесконечные троичные и т.д. дроби. Чтобы понятие действительного числа не зависело от формы записи, формулируют аксиомы, которым они удовлетворяют. Можно предложить несколько аксиоматик действительного числа. Одним из примеров может служить система аксиом, опирающаяся на свойства сложения. В ней неопределяемые понятия – это единица, операция сложения. Названные понятия должны удовлетворять следующей системе аксиом:

1. Множество натуральных чисел является подмножеством множества положительных действительных чисел. ( )

2. Операция сложения ставит в соответствие любой паре действительных чисел a и b число , называемое суммой чисел.

3. Сложение в R₊ коммутативно:

4. Сложение в R₊ ассоциативно:

5.

6.

7.

Аксиомы 1–7 позволяют ввести на множестве положительных действительных чисел отношение порядка:

8. Аксиома непрерывности. Если числовое множество X лежит слева от числового множества Y, т.е. и , то существует число , разделяющее множества X и Y, так, что .

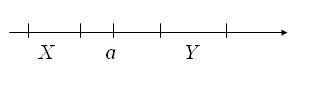
Другую систему аксиом см. в книге Сендер, А.Н. «Методология формирования понятия о числе», с.145.

V. Действительные отрицательные числа. Число 0. Модуль действительного числа

С помощью положительных действительных чисел можно выразить результат измерения любой скалярной величины: длины, площади, объема, массы и т.д. Но на практике часто бывает нужно выразить числом не результат измерения величины, а ее изменение, т.е. показать, на сколько изменилась эта величина. Изменение величины может идти в двух направлениях: она может как увеличиваться, так и уменьшаться, а может и остаться неизменной. Поэтому, чтобы выразить изменение величины, кроме положительных действительных чисел, нужны иные числа, нужно расширить множество R₊. Мы расширим его, присоединив к нему число 0 (ноль) и отрицательные числа. Число 0 характеризует такое состояние при измерении, когда величина не изменяется, остается прежней.

Итак, возьмем множество R₊ положительных действительных чисел и поставим в соответствие каждому числу х из R₊ новое число, которое будем обозначать –х (читается «минус х»). Например, числу 5 ставится в соответствие число –5, числу 8,14 — число –8,14 и т.д. Числа вида –х, где , назовем отрицательными числами, а их множество обозначим R_–.

Определение. Множеством действительных чисел называется объединение множества положительных действительных чисел с множеством отрицательных действительных чисел и 0. , причем множества R_–, R и {0} попарно не пересекаются (ни одно число не может быть одновременно и положительным, и отрицательным; или и положительным, и нулем).

Между множеством действительных чисел и множеством точек координатной прямой существует взаимно-однозначное соответствие, т.е. каждому действительному числу соответствует вполне определенная и единственная точка на координатной прямой. И наоборот: каждой точке соответствует определенное единственное действительное число.

При этом непрерывность числовой прямой является подтверждением непрерывности множества действительных чисел. Это значит, что на прямой не существует точки, которая не соответствовала бы какому-либо действительному числу.

Определение. Все точки на координатной прямой, расположенные правее точки 0, соответствуют положительным действительным числам, а все точки левее точки 0 – отрицательным.

Числа х и (–х), где , изображаются точками координатной прямой, симметрично расположенными относительно начала отсчета 0. Эти числа называют противоположными друг другу, причем считают, что –(–х) = х. Например, –(–6) = 6. Число 0 считают противоположным самому себе: – 0 = 0.

Множество действительных чисел является бесконечным, т.е. не существует наименьшей и наибольший элемент. Оно имеет мощность континуума.

Множество R упорядочено, несчетно.

Определение. Модулем действительного числа называется расстояние от точки 0 до точки, изображающей это число. Геометрический смысл модуля:

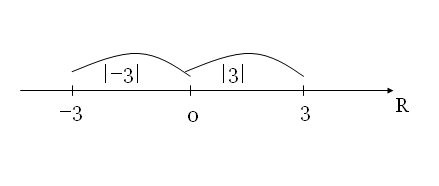
Поскольку расстояние есть величина неотрицательная, то модуль любого числа тоже выражается неотрицательным числом.