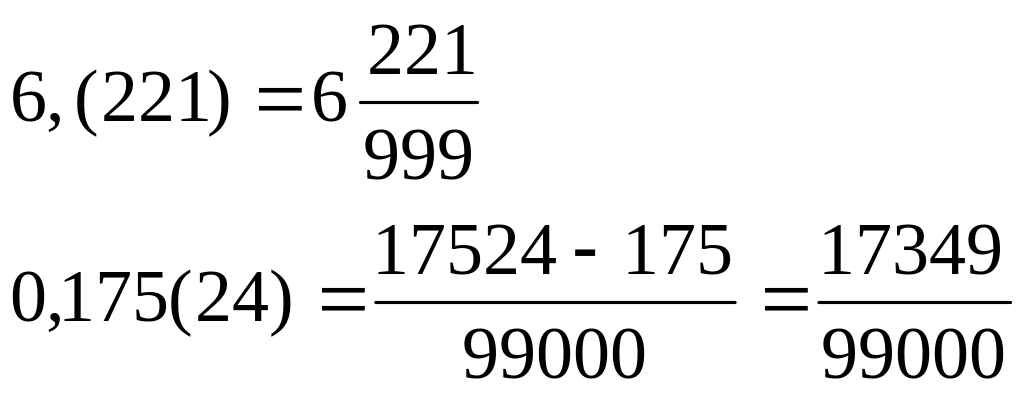- •Теория рационального числа
- •I. Задачи, приводящие к введению рациональных чисел
- •II. Измерение отрезков. Обыкновенная дробь. Классификация обыкновенных дробей.
- •III. Равные дроби. Признак равенства дробей
- •VI. Основное свойство дроби.
- •VII. Использование основного свойства дроби
- •VIII. Действия над рациональными числами
- •IX. Свойства сложения рациональных чисел
- •X. Разность положительных рациональных чисел
- •XVI. Различные формы записи рациональных чисел. Десятичные дроби
- •XVII. Равные десятичные дроби. Правила сложения и умножения десятичных дробей
- •XVIII. Проценты
- •XIX. Преобразование обыкновенных дробей в десятичную. Бесконечные десятичные периодические дроби
- •Величины
- •I. Определение величины
- •II. Аксиоматическое определение величины
- •III. Измерение величин
- •Длина отрезка и ее измерения
- •II. Площадь фигуры и ее измерение
- •III. Равные и равновеликие фигуры
- •IV. Прямое и косвенное измерение площадей
- •IV. Величины в начальном курсе математики
- •Теория действительных чисел
- •I. Несоизмеримые отрезки. Иррациональные числа
- •II. Действия на иррациональными числами
- •III. Умножение положительных иррациональных чисел
- •IV. Аксиоматика множества положительных действительных чисел
- •V. Действительные отрицательные числа. Число 0. Модуль действительного числа
- •VI. Свойства модуля
- •VII. Вычитание и деление на множестве действительных чисел
- •VIII. Операция деления
- •IX. Правило деления
XVIII. Проценты
Определение. Процент – сотая часть любого числа.
Виды задач на проценты:
1. Нахождение процента от числа.
Население города 300000 человек, 70% - женщины. Сколько женщин в городе?
![]() (человек)
(человек)
2. Нахождение числа по его проценту.
В городе 210000 женщин, что составляет 70% населения. Какого население города?
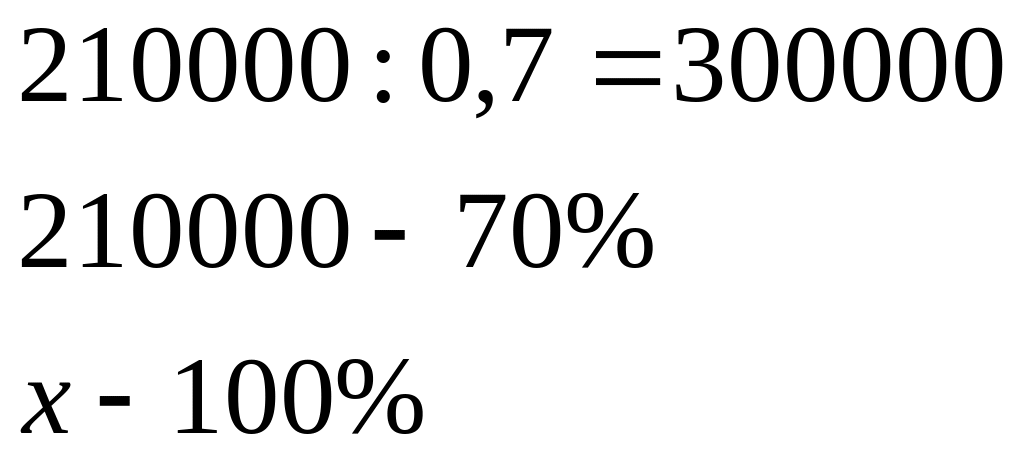
3. Нахождение процентного отношения двух чисел.
Население города 300000 человек, из них 210000 – женщины. Сколько процентов населения составляет женщины?
210000:300000=0,7(70%).
Промилле – тысячная часть от числа (‰).
XIX. Преобразование обыкновенных дробей в десятичную. Бесконечные десятичные периодические дроби
Обратить десятичную дробь в обыкновенную не составляет труда. Для этого записывают целую часть, затем в числителе записывают число, стоящее после запятой, а в знаменателе – степень числа 10, причем показатель степени равен количеству цифр, стоящих после запятой.
Для того, чтобы обратить обыкновенную дробь в десятичную, поступают одним из следующих способов.
1. Умножают числитель и знаменатель на такое число, чтобы в знаменателе получилось степень 10. Используется, если в знаменателе небольшие числа.
![]()
2. Делением числителя на знаменатель. Таким образом, получаем десятичную дробь. При этом в процессе деления может получиться конечная десятичная дробь, либо бесконечная десятичная дробь. Бесконечная дробь может быть периодической либо непериодической.
Определение. Бесконечной периодической десятичной дробью называется дробь, в которой, начиная с некоторого знака после запятой, одна цифра или группа цифр повторяется.
0,333…=0,(3)
0,54333…=0,54(3)
Для того, чтобы узнать, переводится ли обыкновенная дробь в конечную или нет, пользуются следующей теоремой.
ХХ
Теорема 1.
Несократимая обыкновенная дробь
![]() ,
переводится в конечную десятичную дробь
тогда и только тогда, когда, в разложении
знаменателя этой дроби присутствуют
только степени числа 2 или 5.
,
переводится в конечную десятичную дробь
тогда и только тогда, когда, в разложении
знаменателя этой дроби присутствуют
только степени числа 2 или 5.
Доказательство.
1. Необходимость. Докажем теорему: если несократимая обыкновенная дробь представима в виде десятичной, то в разложении знаменателя присутствуют степени только 2 или 5.
Действительно,
если дробь
представима в виде десятичной, то ее
можно записать в виде
![]() .
.
2. Достаточность. Дано, что несократимая дробь представима в виде десятичной дроби, в разложении знаменателя которой содержатся множители 2 или 5. Нужно доказать, что может быть представлена в виде конечной десятичной дроби.
![]() ,
при
,
при
![]()
Если
![]() ,
то домножим числитель и знаменатель на
,
то домножим числитель и знаменатель на
![]() .
.
![]()
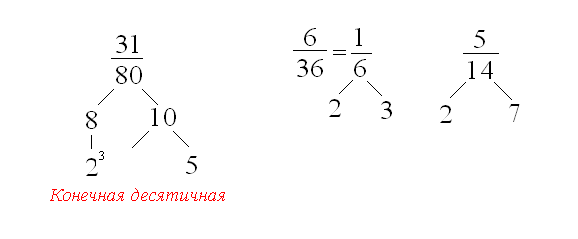
Кроме конечных, существуют бесконечные десятичные дроби: периодические и непериодические. Периодические делятся на чистые и смешанные.
Определение. Десятичной бесконечной чистой периодической дробью называют такую десятичную дробь, у которой период начинается сразу после запятой.
0,(3); 0,(527)
Определение. Десятичной бесконечной смешанной периодической дробью называется дробь, у которой сразу после запятой стоит одна или несколько цифр, называемых предпериодом, а затем следует период.
3,27(625)
ХХ1
Теорема 2. Несократимая дробь переводится в чистую периодическую дробь, если в разложении знаменателя этой дроби имеются любые простые множители, за исключением 2 и 5.
![]()
Замечание. Число цифр в периоде чистой периодической дроби не превышает ее знаменателя, т.е. если в знаменателе число b, то в периоде может быть 0,1,2…(b-1) цифр.
Теорема 3. Обыкновенная несократимая дробь переводится в смешанную периодическую в том случае, если в разложении знаменателя этой дроби есть множители 2 или 5 и плюс еще любые простые числа.
![]()
Замечание. При переводе обыкновенной дроби в десятичную важным условием является требование о несократимости данной дроби.
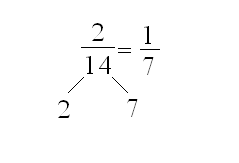
Определение. Положительное рациональное число – множество дробей, представляющих длину одного и того же отрезка.
Определение. Положительным рациональным числом называется бесконечная периодическая десятичная дробь.
Оказывается, что не только обыкновенная дробь может быть переведена в десятичную, но и десятичная дробь с помощью определенных правил переводится в обыкновенную.
ХХ11
Правило 1 (Правило перевода чистой периодической десятичной дроби в обыкновенную). Чтобы чистую периодическую десятичную дробь перевести в обыкновенную, необходимо в числителе записать число, образованное цифрами периода, а в знаменателе – столько девяток, сколько цифр в периоде.
![]()
Доказательство.
Пусть 0,(36)=а
Найдем 100а=36,(36)
100а=36+а
100а – а=36
99а=36
![]()
ХХ11
Правило 2 (Правило перевода смешанной периодической дроби в обыкновенную). Чтобы смешанную периодическую дробь перевести в обыкновенную, нужно в числителе записать разность между числом, записанном цифрами, стоящими до 2го периода и числом, записанным цифрами предпериода. В знаменателе записываем число, состоящее из стольких девяток, сколько цифр в периоде и стольких нулей, сколько цифр в предпериоде.
![]()
Доказательство.
Пусть 0,11(36)=а
Найдем 100а=11,36
10000а=1136,(36)
10000а=1136+0,(36)


11,(36) – 11
10000а=1136+100а–11
9900а=1136–11
![]()
Любое рациональное
число представимо в виде бесконечной
периодической десятичной дроби, в т.ч.
и натуральные числа (![]() )
)
![]()
Непериодические дроби – множество иррациональных чисел (I)
![]()