VI. Основное свойство дроби.

Теорема 4. Числитель и знаменатель дроби можно разделить и умножить на одно и то же натуральное число. В результате получим дробь, равную данной.

Доказательство. Возьмем дробь . Пусть m=km₁

n=kn₁

Докажем, что

По теореме 1:

Домножим:

Левые и правые части равны, т.е. дроби .

Теорема доказана

VII. Использование основного свойства дроби

Основное свойство дроби используется при сокращении дробей и приведении их к общему знаменателю.

Сократить дробь – это значит заменить дробь равной ей дробью, но с меньшим числителем и знаменателем. Существует 2 приема сокращения дробей:

1. Последовательное сокращение на небольшие числа, которые являются общими делителями числителя и знаменателя.

2. Сокращение числителя и знаменателя на них НОД.

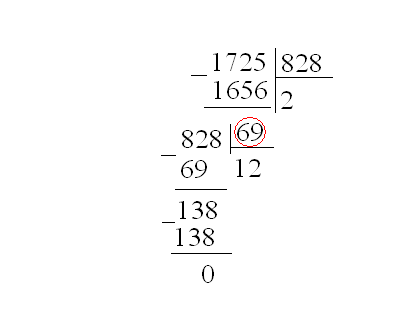
Привести дроби к общему знаменателю – значит заменить данные дроби равными им дробями, имеющие одинаковые знаменатели. Общий знаменатель двух дробей является их НОК.

и

НОК(28; 42)=

Таким образом, можно сформулировать следующий алгоритм приведения чисел к наименьшему общему знаменателю:

1. Найти НОК знаменателей данный дробей.

2. Найти дополнительные множители для каждой дроби путем деления НОК на соответствующий знаменатель.

3. Умножение числителя и знаменателя каждой дроби на соответствующий дополнительный множитель.

VIII. Действия над рациональными числами

1. Сумма положительных рациональных чисел.

Определение. Суммой 2х положительных рациональных чисел с одинаковыми знаменателями и называется рациональное число с тем же знаменателем и числителем, равным сумме числителей слагаемых .

Теорема 5. Сумма рациональных чисел не зависит от выбора представителей из классов равных дробей.

Доказательство. Пусть даны рациональные числа и . Возьмем для каждой из данных дробей еще по одному представителю из их классов, т.е. и .

Докажем, что .

По определению суммы: ,

Из равенств и следует:

Сложим эти равенства почленно:

Теорема доказана.

IX. Свойства сложения рациональных чисел

Свойство 1. Сложение целых неотрицательных чисел является частными случаем сложения дробей с одинаковыми знаменателями.

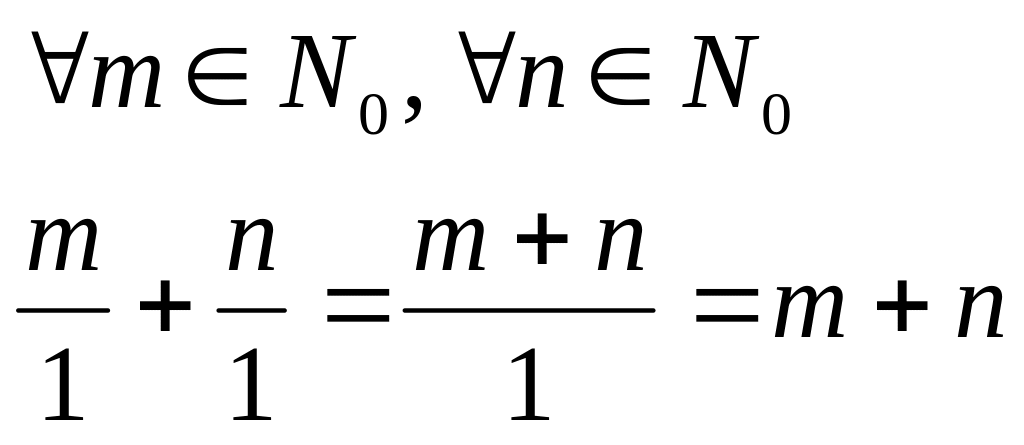
Свойство 2. Сумма двух положительных рациональных чисел всегда существует.

Доказательство основано на том, что любые две дроби можно привести к общему знаменателю.

Свойство 3. Сумма двух рациональных положительных чисел единственна.

Доказательство этого факта вытекает из того, что нахождение суммы двух рациональных чисел сводится к действиям над натуральными числами m, n, p, q.

Свойство 4. Сложение чисел на Q₊ коммутативно.

Доказательство.

Свойство 5. Сложение на Q₊ ассоциативно.

Пусть все дроби приведены к одному знаменателю:

X. Разность положительных рациональных чисел

Разность во множестве положительных рациональных чисел определяется аналогично разности во множестве целых неотрицательных чисел, т.е. как операция, обратная сложению.

Определение. Разностью положительных рациональных чисел и называется такая дробь , что .

Выведем из этого определения правило вычитания дробей (положительных рациональных чисел). Будем считать, что данные дроби уже имеют одинаковые знаменатели (или уже приведены к общему знаменателю).

Разделив обе части этого равенства на n, получим:

p+r=m, где

Таким образом, вычитание положительных рациональных чисел сводится к вычитанию натуральных чисел, а значит, обладает всеми свойствами вычитания натуральных чисел.

1. Если разность существует (при условии, что ), то она единственна.

2. Правило вычитания числа из суммы. Для любых чисел можно записать:

3. Правило вычитания суммы из числа. Для любых положительных рациональных чисел a, b и c можно записать:

XI. Умножение на Q₊

Определение. Произведением положительных рациональных чисел и называется рациональное число .

Теорема 6. Произведение рациональных чисел не зависит от выбора дробей, которые их представляют.

Доказательство. Возьмем ,

Предположим, что . Тогда по теореме 1: .

Поскольку и равные дроби, то применим к ним критерий равенства дробей: .

Домножим первое равенство на pq₁:

Домножим первое равенство на nm₁:

Отсюда по критерию равенства дробей:

Теорема доказана.

Т.к. умножение на множестве Q₊ сводится к действиям над натуральными числами, то свойства умножения на множествах Q₊ и N совпадают.

:

1. Коммутативность: ab=ba

2. Ассоциативность: a(bc)=(ab)c

3. Дистрибутивность:

XII. Деление на Q₊

Определение. Частным двух положительных рациональных чисел a и b называется такое положительное рациональное число с, для которого выполняется .

Выведем правило деления дробей:

Пусть

– по определению

– по критерию равенства дробей

Воспользуемся коммутативностью умножения положительных рациональных чисел:

Чтобы найти частное двух дробей, нужно первую дробь умножить на дробь, обратную второй. (Две дроби взаимно обратны, если их произведение равно 1).

Таким образом, чтобы разделить 2 дроби, необходимо делимое умножить на дробь, обратную делителю:

При делении смешанных дробей их сначала переводят в неправильные дроби, а затем деление заменяют умножением делимого на дробь, обратную делителю.

Свойства деления:

1. Для любых положительных рациональных чисел всегда существует их частное, причем оно единственно.

2. Деление натуральных чисел – частный случай деления рациональных чисел.

3. Деление суммы на число:

4. Деление произведения на число:

5. Деление числа на произведение:

XIII. Отношение «меньше» на Q₊

Определение. Пусть имеется 2 положительных рациональных числа a и b. Число a будет называться меньшим числа b, если существует такое положительное рациональное число с, которое, будучи сложено с a, дает b.

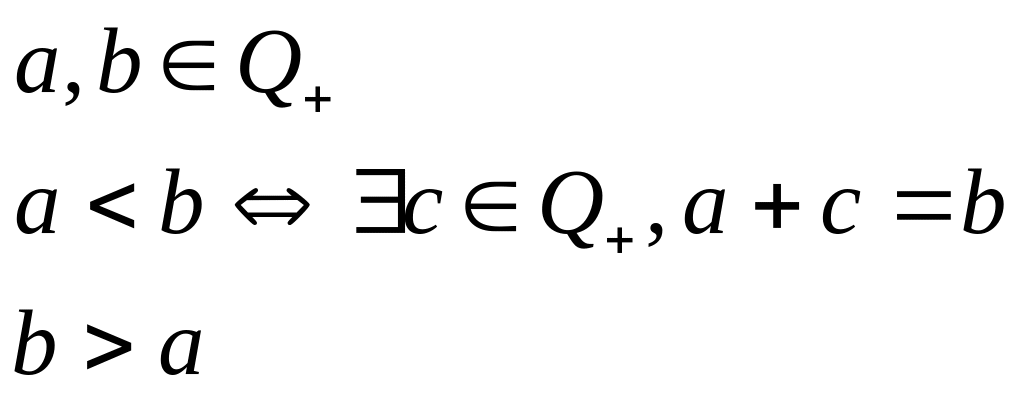
Практические приемы установления отношения «меньше»:

1. Относится к дробям с одинаковыми знаменателями

, т.к.

2. Для дробей с разными знаменателями:

или

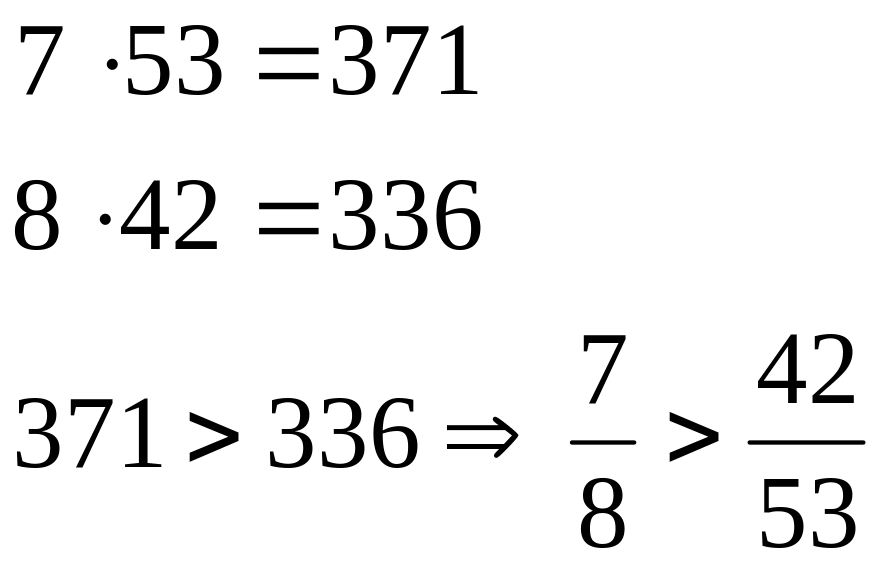
Свойства отношения «меньше» на Q₊:

1. Рефлексивность – не является

– ложно

2. Симметричность – не является

– ложно

– свойство асимметричности

3. Транзитивность - является

– истинно

Таким образом, отношение «меньше» на Q₊ обладает свойствами асимметричности и транзитивности, т.е. является отношением строгого порядка.

XIV.Свойства множества Q₊

1. Q₊ – упорядоченное множество.

Доказательство (см. выше).

2. Множество N – подмножество Q₊.

Каждое натуральное число можно представить в виде , т.е. каждое натуральное число является рациональным.

3. В множестве Q₊ нет наименьшего числа.

Доказательство (методом от противного)

Предположим, что – наименьшее положительное рациональное число. Но всегда можно образовать число . Значит, наше предположение неверно.

4. Множество Q₊ плотно в себе. Т.е. между любыми двумя положительными рациональными числами заключено бесконечное число чисел из Q₊ .

Доказательство.

Возьмем две дроби: и .

Найдем дроби, которые находятся между ними. Для этого найдем среднее арифметическое этих дробей:

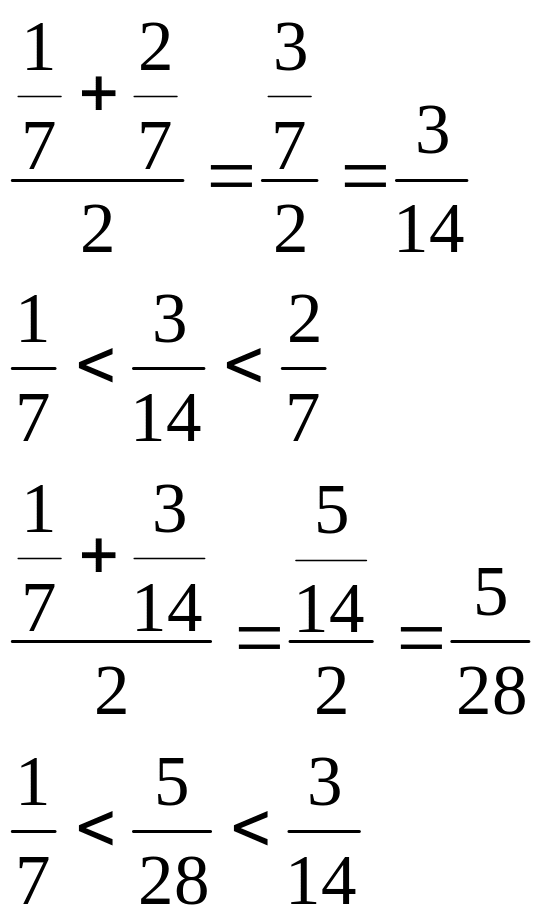
Этот процесс можно продолжать бесконечно.

XV.Множество Q₊ счетно

Определение. Множество называется счетным, если между ним и множеством N можно установить взаимно однозначное соответствие.

Доказательство.

Представим каждое рациональное число в виде дроби. Назовем высотой рационального числа сумму его числителя и знаменателя.

– числа, которые имеют высоту 5.

Расположим все рациональные числа в порядке возрастания высоты, а числа одинаковой высоты - в порядке возрастания числителя. Установим отображение множества Q₊ на множество N.

Таким образом каждому числу из Q₊ мы поставили в соответствие единственное N число. И наоборот: каждому натуральному числу соответствует одно и только одно рациональное число. Т.е. устанавливаемое соответствие является взаимно однозначным или биективным, а множество Q₊ – счетным.