
- •Теория рационального числа
- •I. Задачи, приводящие к введению рациональных чисел
- •II. Измерение отрезков. Обыкновенная дробь. Классификация обыкновенных дробей.
- •III. Равные дроби. Признак равенства дробей
- •VI. Основное свойство дроби.
- •VII. Использование основного свойства дроби
- •VIII. Действия над рациональными числами
- •IX. Свойства сложения рациональных чисел
- •X. Разность положительных рациональных чисел
- •XVI. Различные формы записи рациональных чисел. Десятичные дроби
- •XVII. Равные десятичные дроби. Правила сложения и умножения десятичных дробей
- •XVIII. Проценты
- •XIX. Преобразование обыкновенных дробей в десятичную. Бесконечные десятичные периодические дроби
- •Величины
- •I. Определение величины
- •II. Аксиоматическое определение величины
- •III. Измерение величин
- •Длина отрезка и ее измерения
- •II. Площадь фигуры и ее измерение
- •III. Равные и равновеликие фигуры
- •IV. Прямое и косвенное измерение площадей
- •IV. Величины в начальном курсе математики
- •Теория действительных чисел
- •I. Несоизмеримые отрезки. Иррациональные числа
- •II. Действия на иррациональными числами
- •III. Умножение положительных иррациональных чисел
- •IV. Аксиоматика множества положительных действительных чисел
- •V. Действительные отрицательные числа. Число 0. Модуль действительного числа
- •VI. Свойства модуля
- •VII. Вычитание и деление на множестве действительных чисел
- •VIII. Операция деления
- •IX. Правило деления
Теория рационального числа
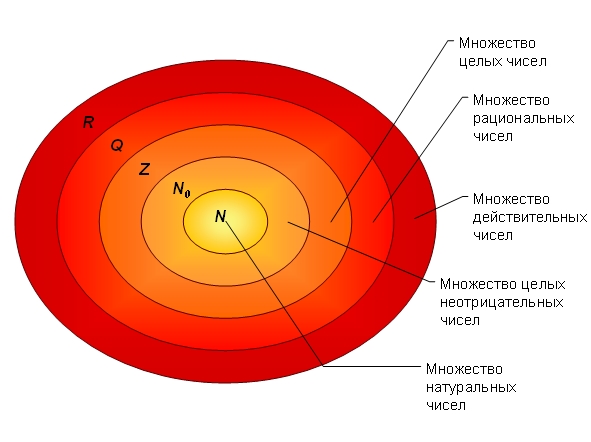
I. Задачи, приводящие к введению рациональных чисел
1. Решение уравнения
вида
![]() .
Это уравнение имеет решение во множестве
целых чисел тогда и только тогда, когда
b
делится на
а.
В случае, если b
не делится
на а, уравнение
неразрешимо в множестве целых чисел.
.
Это уравнение имеет решение во множестве
целых чисел тогда и только тогда, когда
b
делится на
а.
В случае, если b
не делится
на а, уравнение
неразрешимо в множестве целых чисел.
2. Задача измерения
длины отрезка с помощью данной единицы
измерения е.
Не всегда единичный отрезок е
укладывается целое число раз в измеряемом
отрезке. Именно эти задачи исторически
обусловили появление рациональных
чисел, т.е. дробей. Историки утверждают,
что наиболее вероятно, появление дробей
связано с процессом различных измерений:
длины, массы, площади, времени. Возможно,
их возникновение связано с потребностью
делить несколько предметов на количество
частей, большее количества этих предметов
(Например, разделить 3 мешка зерна между
4 людьми). Так на Руси возникли конкретные
меры объема: четверть, осьмушка и т.д.
Из древних папирусов известно, что в
Древнем Египте широко использовались
дроби, которые сейчас называются доли
(т.е. дроби вида
![]() ).
Древние индусы и арабы тоже пользовались
дробями, которые записывались следующим
образом:
).
Древние индусы и арабы тоже пользовались
дробями, которые записывались следующим
образом:
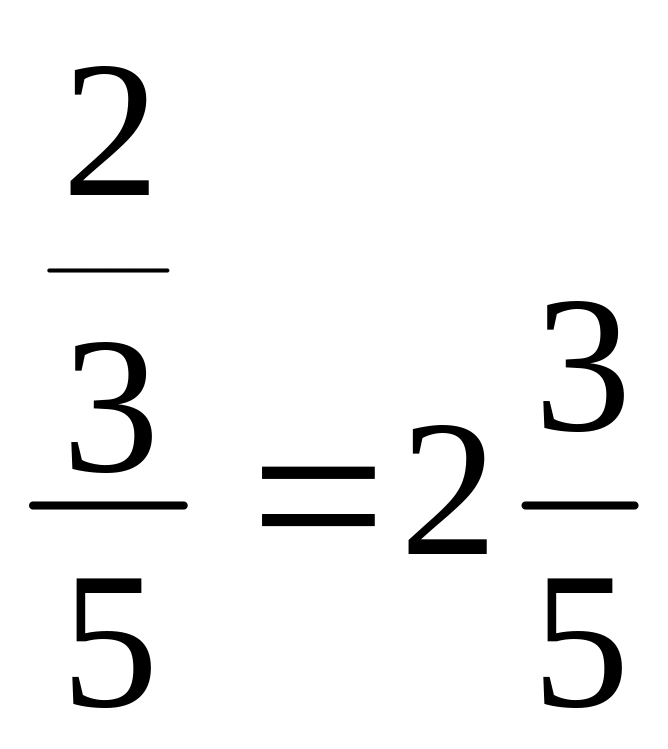 . Только
начиная с XVI
века дроби приобрели современный вид.
. Только
начиная с XVI
века дроби приобрели современный вид.
II. Измерение отрезков. Обыкновенная дробь. Классификация обыкновенных дробей.
Возьмем отрезок
АВ
и некоторый единичный отрезок е.
Измерим АВ
с помощью единичного отрезка е.
Если при измерении единичный отрезок
укладывается в АВ
целое число раз (например, k),
то говорят, что длина отрезка АВ
выражается натуральным числом k:
![]() .
Если же длина отрезка АВ
такова, что она не укладывается в нем
целое число раз, то поступим следующим
образом. Разобьем единичный отрезок е
на n
частей и введем новую единицу измерения
.
Если же длина отрезка АВ
такова, что она не укладывается в нем
целое число раз, то поступим следующим
образом. Разобьем единичный отрезок е
на n
частей и введем новую единицу измерения
![]() .
Пусть е1
укладывается m
раз в длине отрезка АВ,
т.е.
.
Пусть е1
укладывается m
раз в длине отрезка АВ,
т.е.
![]() .
В этом случае для выражения длины отрезка
АВ
используется пара чисел (m,
n),
где вторая компонента n
показывает, на сколько частей разбит
единичный отрезок е,
а первая компонента m
указывает, сколько таких частей
укладывается в АВ.
.
В этом случае для выражения длины отрезка
АВ
используется пара чисел (m,
n),
где вторая компонента n
показывает, на сколько частей разбит
единичный отрезок е,
а первая компонента m
указывает, сколько таких частей
укладывается в АВ.
Определение.
Пара чисел (m,
n)
или
![]() называется обыкновенной дробью, причем
числа m
и n
– натуральные. Число n
– знаменатель дроби (показывает, на
сколько равных частей разделили единицу
измерения). Число m
– числитель (показывает, сколько частей
взяли).
называется обыкновенной дробью, причем
числа m
и n
– натуральные. Число n
– знаменатель дроби (показывает, на
сколько равных частей разделили единицу
измерения). Число m
– числитель (показывает, сколько частей
взяли).
При измерении
отрезка могут получаться дроби вида
![]() ,
,
![]() и т.д. если
длина отрезка равна
,
то это означает, что е
укладывается 2 раза и еще остается
и т.д. если
длина отрезка равна
,
то это означает, что е
укладывается 2 раза и еще остается
![]() часть е.
Но если в качестве единицы измерения
взять
часть е.
Но если в качестве единицы измерения
взять
![]() ,
то длина того же отрезка будет равна
7е1,
т.е.
,
то длина того же отрезка будет равна
7е1,
т.е.
![]() .
.
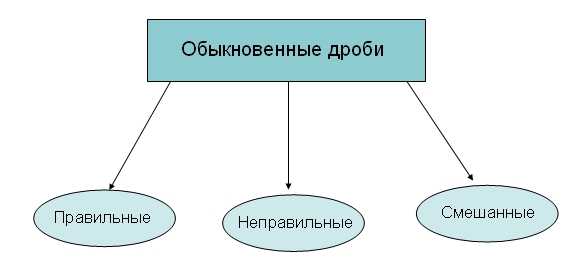
Определение.
Дробь вида
называется
правильной, если
![]() ,
т.е. числитель меньше знаменателя.
,
т.е. числитель меньше знаменателя.
Определение.
Дробь вида
называется
неправильной, если
![]() .
.
Определение. Дробь вида называется смешанной, если она состоит из целой и дробной частей.
Пусть дана
неправильная дробь
,
где
.
Разделим m
на n
с остатком. По теореме о делении с
остатком разделить m
на n
с остатком значит найти такие числа q
и r,
которые удовлетворяют следующему
равенству:
![]() ,
где
,
где
![]() .
Если r=0,
то
.
Если r=0,
то
![]() .
Дробь имеет вид:
.
Дробь имеет вид:
![]() .
Этот процесс называется выделением
целой части из неправильной дроби. Такую
сумму целого числа и правильной дроби
записывают без знака «+» и называют
смешанной дробью. Таким образом каждую
неправильную дробь можно перевести в
смешанную: для этого достаточно числитель
разделить на знаменатель с остатком.
.
Этот процесс называется выделением
целой части из неправильной дроби. Такую
сумму целого числа и правильной дроби
записывают без знака «+» и называют
смешанной дробью. Таким образом каждую
неправильную дробь можно перевести в
смешанную: для этого достаточно числитель
разделить на знаменатель с остатком.
![]()
Верно и обратное: любую смешанную дробь можно перевести в неправильную. Для этого необходимо знаменатель умножить на целую часть и к полученному произведению прибавить числитель.
![]()
