Планирование и обработка эксперимента / Berestneva - Prikladnaya statistika 2012

Окончание табл. 3.5

Рис. 3.8. Результаты вычисления и выводы

3.2. Непараметрические меры связи

3.2.1. Коэффициент корреляции рангов

Из непараметрических показателей связи наиболее широкое применение нашел коэффициент корреляции рангов, предложенный Спирменом [15]:

n

6 di2

rs 1 n ni 1 1 , (3.8)

2

121

где di Rx Ry – разность между рангами признаков x и y; n – число

парных членов ряда или объем выборки.

В основу конструкции этого показателя положены весьма простые соображения. Ранжируя попарно связанные значения признаков, можно видеть, как они распределяются относительно друг друга. Если возрастающим значениям одного признака x соответствуют возрастающие значения другого y, то между ними существует положительная связь. Если же при возрастании значений одного признака значения другого последовательно уменьшаются, это указывает на наличие отрицательной связи между ними. При отсутствии корреляции ранжированным значениям одного признака будут соответствовать самые различные значения другого.

Обозначив ранжированные значения признаков порядковыми числами 1, 2, 3, 4, …, нетрудно определить ранги этих значений и по их разностям судить о степени зависимости одного признака от изменений другого. Очевидно, при полной связи ранги коррелируемых признаков совпадут и разность между ними будет равна нулю. В таких случаях коэффициент корреляции рангов окажется равным единице. Если же при-

и коэффициент корреляции рангов будет равен нулю. Таким образом, коэффициент корреляции рангов выражается в долях единицы и может принимать значения от –1 до + 1, т. е. сопровождается положительным или отрицательным знаком.

Значимость этого показателя оценивают путем сравнения выборочного коэффициента rs с критической точкой rst, которую можно определить по формуле

где n – объем выборки; t и т – величины, связанные, с уровнем значимости следующим образом: для = 5 %, t = 1,96 и т = 0,16; для= 1 %, t = 2,58 и т = 0,69. Нулевую гипотезу отвергают, если эмпирически найденная величина rэмп превзойдет или окажется равной критическому значению rкр для принятого уровня значимости и объема выборки n. Чтобы каждый раз не рассчитывать критические точки rкр, составлена специальная таблица (см. [6, 24]).

Приведенный способ оценки значимости выборочного rэмп не единственный. При n 10 значимость эмпирического коэффициента корре-

122

ляции рангов можно оценить с помощью t-критерия Стьюдента, т. е. по отношению этого показателя к своей статистической ошибке

в виду, что на его значении сказывается наличие групп с одинаковыми рангами, и тем сильнее, чем больше таких групп среди сопряженных значений признаков x и y. Чтобы получить более точное значение rэмп, нужно при наличии указанных групп вносить поправку в формулу (3.8). Эту поправку, обозначаемую буквой Т, прибавляют к числителю формулы, т. е.

где T = Vx + Vy, a Vx – поправка для одного признака (ряд х), Vy – для другого (ряд у). Для определения Vx и Vy составлена специальная таблица (табл. 3.6), в которой l обозначает число групп с одинаковыми рангами (столбцы), а t – число рангов в этих группах (строки).

Пример 3.2

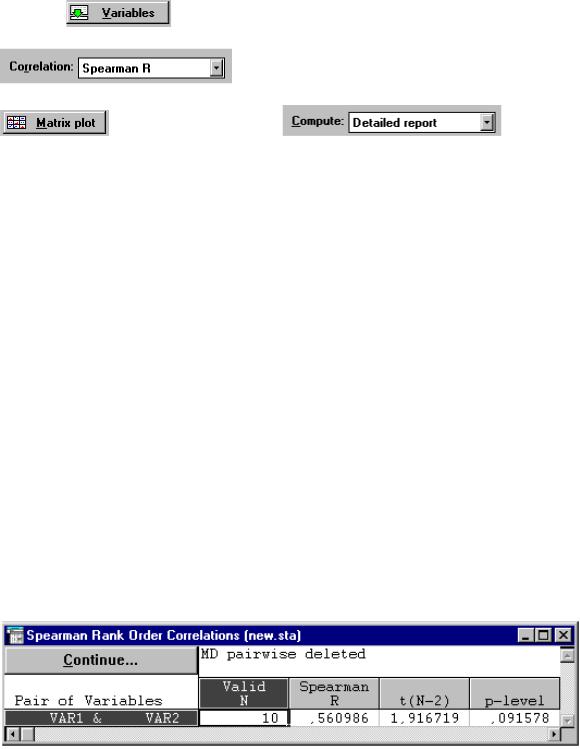
Рассмотрим способ вычисления рангового коэффициента корреляции Спирмена в прикладном статистическом пакете STATISTICA (для работы в пакете SPSS порядок действий описан в примере 3.1). Воспользуемся данными табл. 3.7 и вычислим коэффициент корреляции рангов между шкалами тревожности и агрессивности теста ММРI.

Для того чтобы получить значения рангового коэффициента корреляции, активизируйте модуль Nonparametric Statistics. Загрузите файл данных. Выберите пункт Correlations (Spearman, Kendall tau, gamma) из предложенного меню и завершите выбор нажатием кнопки OK. В открывшемся диалоговом окне задайте параметры корреляционного анализа. Для того чтобы выбрать исследуемые признаки, нажмите

123

Подставляя известные значения в формулу (4.4), находим:

Полученная величина указывает на наличие тесной связи между ответами по двум тестам. Значимость этого показателя ( кр2 = 100(0,731)2 =

= 53,44) значительно превышает критический уровень кр2 = 10,83 для

= 0,1 % иv = 1.

3.2.3. Коэффициент взаимной сопряженности

Для определения степени сопряженности между качественными признаками с числами вариантов, большими двух, служит коэффициент взаимной сопряженности или полихорический показатель связи, предложенный К. Пирсоном:

клетках многопольной корреляционной таблицы, а fx и fy – суммы частот по строкам и столбцам той же таблицы; N = fx + fy – общая сумма частот, или объем выборки.

Пирсоновский коэффициент взаимной сопряженности (С) имеет один существенный недостаток: его значение значительно зависит от количества вариант коррелируемых качественных признаков.

Учитывая этот недостаток, А.А. Чупров внес поправки в формулу (3.12) и получил следующее выражение [17]:

Здесь К – коэффициент взаимной сопряженности Чупрова; nx и ny – численность групп по строкам и столбцам многопольной таблицы; N –

126

объем выборки. Остальные символы объяснены выше. Нулевую гипотезу отвергают, если эмп2 N 2 кр2 для принятого уровня значимости и числа степеней свободы.

Пример 3.4 [15]

Изучали зависимость между цветом волос и цветом глаз у человека. Результаты наблюдений сведены в табл. 3.9.

Определим коэффициент взаимной сопряженности между этими признаками, предварительно рассчитав величину 2:

Так как эмп2 кр2 нулевая гипотеза отвергается на весьма высоком

уровне значимости (р < 0,001).

Необходимо помнить, что правильное применение критерия 2 основано на требовании, чтобы в клетках корреляционной таблицы содержалось не менее пяти вариантов и общее число наблюдений не было меньше 50. Несоблюдение этих требований не гарантирует получение достаточно точных оценок генерального параметра 2 , а следовательно, и правиль-

ных выводов, которые делают на основании выборочных показателей.

127

показателей, соответствующих полярным различиям базовых параметров, свидетельствует о наличии зависимости между ними. Мера линейности этой связи определяется по результатам вычислений, при которых вспомогательный параметр рассматривается как базовый, а базовый – как вспомогательный. В отличие от корреляционного анализа при таком методе математической обработки результатов исследования не утрачиваются численные значения анализируемых параметров и одновременно устанавливается характер связи между ними.

В табл. 3.10 приведены сведения о том, какой из коэффициентов корреляции следует использовать в зависимости от того, в каких шкалах измерены исследуемые переменные.

129

Окончание табл. 3.8

130