Процедура mcch

procedure MCCH( M:raM100_10; MK:raX;N,Q:integer;var X:raX);

позволяет получать числа со следующими законами распределения:

1) изменение параметров с равномерным шагом

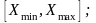
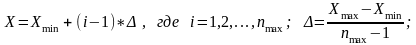
2) равномерное распределение на интервале

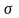
3) нормальное распределение с параметрами и ;

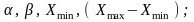
4) бета-распределение с параметрами

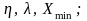
5) гамма-распределение с параметрами

6) Экспоненциальное распределение получается из гамма-распределения при =1.

Значение формальных параметров процедуры:

М - массив , задающий режим работы процедуры (см. табл.1);

МК - массив констант, вычисляемых в процедуре OGR;

N - номер реализации;

Q - количество элементов входного (случайного) вектора X;

Х - случайный вектор (выходной массив процедуры).

Процедура MCCH использует при работе датчик равномерно распределённых на интервале [0, l] случайных чисел. Работа процедуры основана на формировании чисел с заданным законом распределения методом исключения (метод Дж. фон Неймана). Закон распределения описывается в простейшей форме, и случайное число приводится к закону распределения с заданными параметрами по формуле линейного преобразования одномерной случайной величины:

пусть Х - случайное число, Y = a Х + b;

т огда

Вывод рабочих формул (R – равномерно распределенное на интервале [0…1] случайное число):

1 . Равномерное распределение на интервале по формуле:

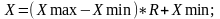
2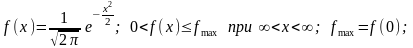 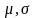. Нормальное распределение с параметрами . Простейшая формула плотности нормального распределения (м.о.=0 и с.к.о.=1) имеет вид:

П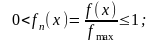 ри методе Неймана используется нормированная (приведенная) плотность распределения

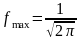
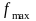
Коэффициент нормировки равен

Отсюда с учётом правила „3”:

По формуле линейного преобразования производится переход к требуемому

з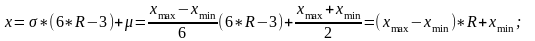 акону распределения:

З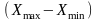 начения и вычисляются в процедуре OGR. по правилу "3".

3. Бета-распределение при 0x1 имеет вид:

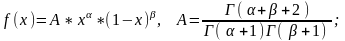
(3.1)

где

Точку максимума функции находим, приравнивая нулю первую производную

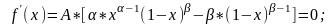
Е 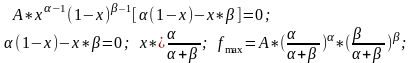сли 0<x<1 , 0, 0 , то

где – коэффициент нормировки.

Нормированная плотность распределения равна:

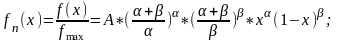
При =0, 0 или 0, =0 , получаем степенную функцию

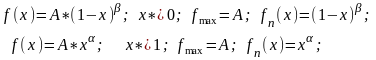
П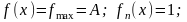 ри =0, =0; получаем равномерную плотность распределения:

В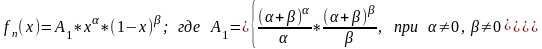 общем случае можно записать:

П ри программной реализации в случае в процедуре OGR происходит изменение соответствующего элемента задающего массива (К[J]:=1).

П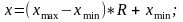 ереход к общему случаю бета-распределения осуществляется по формуле

где R выбирается по методу Неймана с учетом плотности (3.1).

4. Гамма-распределение имеет в простейшем виде (=1) следующую плотность распределения

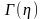
Для расчёта функции // вычисление значения Гамма функции

используется разложение Гаусса в бесконечное произведение

( см. Р.Курант, Краткий курс дифференциального и интегрального исчисления, т.2,стр.355,изд.»Наука», Москва 1970г. )

procedure Fgamma (X :extended; var gamma:extended );

Число сомножителей N=10000.

Результаты счёта : G(5)= 23,9760179882471- точное значение -24;

G(6)= 119,820185838726- точное значение -120;

Для выбора числа N были проведены расчёты разных значений N.

Был проведен расчет при N=100000.

Результаты счёта : G(5)= 23,9976001799882- точное значение -24;

G(6)= 119,982001859839- точное значение -120;

Был проведен расчет при N=1000000.

Результаты счёта : G(5)= 23,9997600018 - точное значение -24;

G(6)= 119,9982000186- точное значение -120;

Был выбран вариант– N=10000. Ошибка не превышает 1Е-3

Задается в виде Fgamma ( teta,gamma );

К общему виду (см. табл.2) эту плотность распределения приводит линейное преобразование

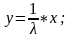
Следовательно, при формировании чисел, имеющих γ-распределение, можно использовать функцию (4.1) с последующим линейным преобразованием (4.2).

При выводе рабочей формулы воспользуемся тем же методом, что и в п.З:

Окончательно имеем:

Д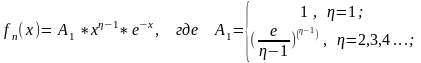 алее, поскольку гамма-распределение справа не ограничено, а метод Неймана рассматривается на конечном интервале, необходимо оценить границу распределения при заданной доверительной вероятности Р_дов ,

Д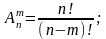 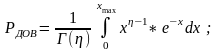ля целых имеем:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

где

Ч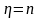 исленное решение уравнения при

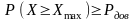
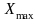
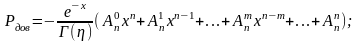
Получим значение такое, что .

С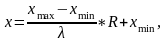 учетом формул линейного преобразования имеем

где R выбирается по методу Неймана с учетом плотности (4.1).

1. Экспоненциальное распределение получается из (4.1) при =1.