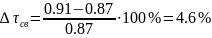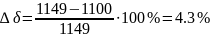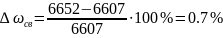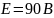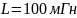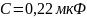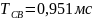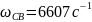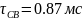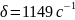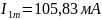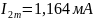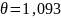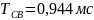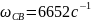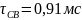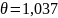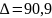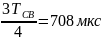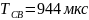Лабораторная №15
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИСТЕТ»

Инженерной школы энергетики
Отделение электроэнергетики и электротехники
Лабораторная работа №15
КОЛЕБАТЕЛЬНЫЙ ПРОЦЕСС В ЦЕПИ ВТОРОГО ПОРЯДКА
Вариант 8
Исполнитель:
|
|
||||||||
студент группы 5А8Д |
|
|
Нагорнов А.В. |
|
|
||||
|
|
|
|
|
|
||||
Руководитель:
|
|
||||||||
к.т.н., доцент ОЭЭ ИШЭ |
|
Колчанова В. А.
|
|
|
|||||
|
|
|
|
|
|
||||
Томск 2020
Цель работы: экспериментальное исследование колебательного переходного процесса в цепи с последовательным соединением R, L, С при включении ее на постоянное напряжение.
Схема цепи
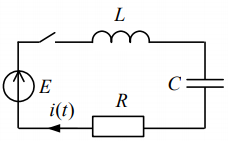
Рисунок 1

Рисунок 2
Дано:
Таблица 1
Вариант |
8 |
|
E |
В |
90 |
L |
мГн |
100 |
C |
мкФ |
0,22 |
R |
Ом |
220 |
Подготовка к работе
1. Как составляется характеристическое уравнение?
Характеристическое уравнение получают заменой
 на
на
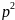 , а
, а
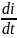 на p,
на p,
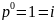
2. Какие переходные режимы возможны в цепи R, L, C в зависимости от вида корней характеристического уравнения?
Возможны 3 случая:
1) Корни вещественные, различные, отрицательные – апериодический процесс;
2) Корни комплексно-сопряжённые – колебательный процесс;
3) Корни вещественные, отрицательные и равные – критический процесс.
3. Как определяются независимые и зависимые начальные условия? Определить i(0), uC (0), uL(0), i'(0) для схемы рис. 1
Для данной схемы определим зависимые и независимые начальные условия:
ННУ:
т.к.
ключ разомкнут, то
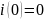

ЗНУ:

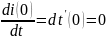
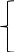 4.
Как определяются постоянные интегрирования
в выражении для свободных составляющих?
4.
Как определяются постоянные интегрирования
в выражении для свободных составляющих?
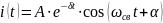

=>
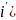
=>
5. Как по значению комплексного корня определить постоянную времени огибающей и период свободных колебаний? Как те же величины найти по осциллограмме?
Постоянная
времени огибающей:
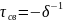
Период
свободных колебаний:
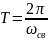
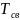 -
Длина
одного периода колебаний;
-
Длина
одного периода колебаний;
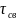 -
Длина
под касательной к огибающим;
-
Длина
под касательной к огибающим;
6. Что такое декремент колебания, как он вычисляется и что характеризует?
Декремент колебаний – величина, которая характеризуем скорость колебательного процесса (скорость затухания).
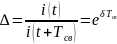
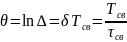

Ход работы
Таблица 2
Параметры цепи |
|
|
|
|
Из осциллограмм |
|
|
|
|
Расчет |
|
|
|
|
Расчет для осциллограммы
Логарифмический декремент:
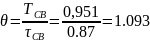
Коэффициент затухания:
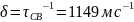
Угловая частота свободных колебаний:
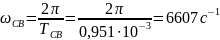
Декремент колебания:
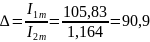
Осциллограмма при R=220 Ом
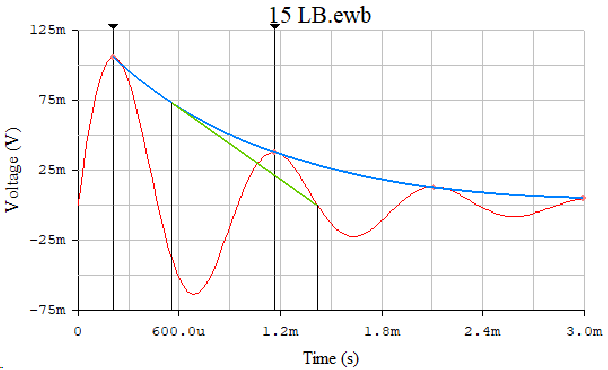
Рисунок 3
Аналитический расчет
Корни характеристического уравнения:
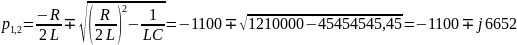
Коэффициент затухания:
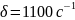
Угловая частота свободных колебаний:
Период свободных колебаний:
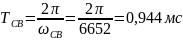
Постоянная времени огибающей:

Логарифмический декремент:

Постоянная интегрирования:

Ток при колебательном процессе:
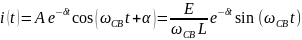

Рассчитаем
по этой формуле значения тока в моменты
времени
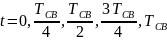 и построим расчетную кривую в одних
осях с осциллограммой.
и построим расчетную кривую в одних
осях с осциллограммой.
Таблица 3
t |
0 |
|
|
|
|
|
0 |
104 мА |
0.148 мА |
-62 мА |
-0.176 мА |
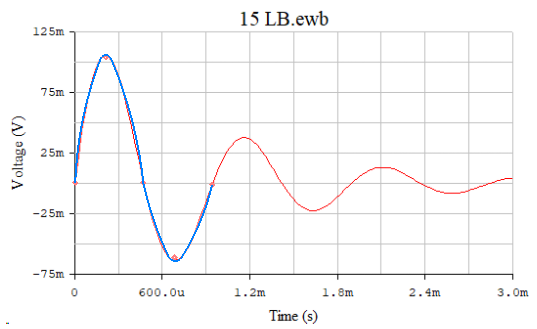
Рисунок 4

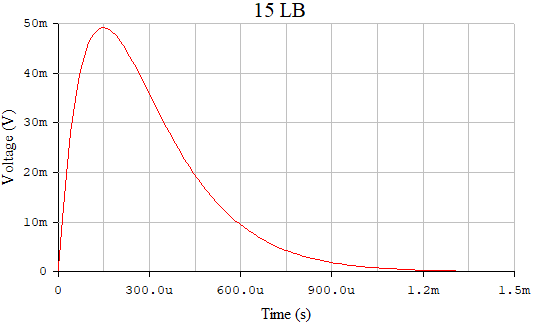
Рисунок 5 – Осциллограмма при R = Rкр
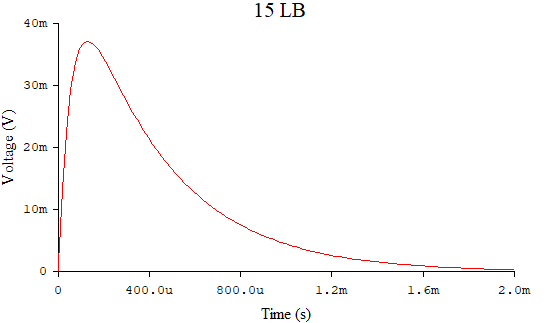
Рисунок 6 – Осциллограмма при R = 2000 Ом > Rкр
Вывод
В ходе лабораторной работы было проведено экспериментальное исследование колебательного переходного процесса в цепи с последовательным соединением R, L, С при включении ее на постоянное напряжение. Сняты осциллограммы при R=220 Ом, R=Rкр, R>Rкр. Рассчитана формула для нахождения тока при колебательном процессе, а также построена зависимость тока от времени в одних осях с осциллограммой. Точки графика совпали с осциллограммой с минимальной погрешностью.
Относительные погрешности вычислений и эксперимента составляют: